In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 Triangles Ex 6.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 Triangles Ex 6.2
Question 1.
In figures (i) and (ii), DE || SC. Find EC in (i) and AD in (ii).
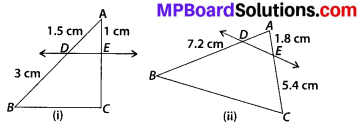
Solution:
(i) Since DE || BC [Given]
∴ Using the Basic proportionality theorem,
We have \(\frac{A D}{D B}=\frac{A E}{E C}\)
Since, AD = 1.5 cm, DB = 3 cm and AE = 1 cm,
∴ \(\frac{1.5 \mathrm{cm}}{3 \mathrm{cm}}=\frac{1 \mathrm{cm}}{E C}\)
By cross-multiplication, we have
EC × 1.5 = 1 × 3
⇒ EC = \(\frac{1 \times 3}{1.5}=\frac{1 \times 3 \times 10}{15}\)
EC = 2 cm
(ii) In ∆ABC, DE || BC
Using the Basic proportionality theorem,

∴ AD = 2.4 cm.
Question 2.
E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR;
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:
(i) We have, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
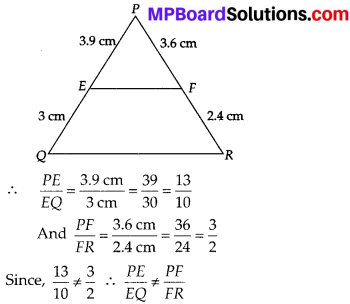
⇒ EF is not parallel to QR.
(ii) We have, PE = 4 cm, QE = 4.5 cm PF = 8 cm and RF = 9 cm
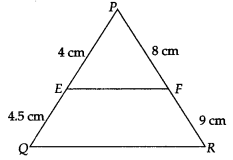
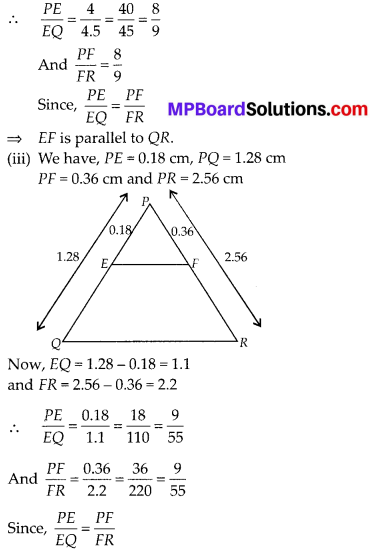
⇒ EF is parallel to QR.
![]()
Question 3.
In the figure, if LM || CB and LN || CD, prove that \(\frac{A M}{A B}=\frac{A N}{A D}\)
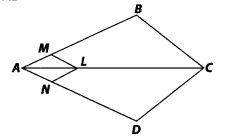
Solution:
In ∆ABC, LM || CB [given]
∴ Using the Basic proportionality theorem, we have
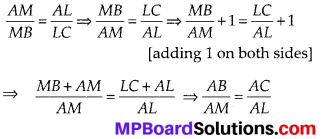

Question 4.
In the figure, DE || ACand DF || AE.
Prove that \(\frac{B F}{F E}=\frac{B E}{E C}\)
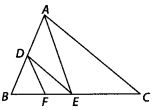
Solution:
In ∆ABC
∵ DE || AC [given]
Using the basic proportionality theorem, we have

Question 5.
In the figure, DE || OQ and DF || OR. Show that EF || QR.
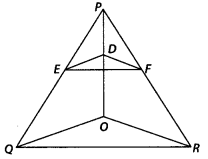
Solution:
In ∆PQO,
∵ DE || OQ [given]
∴ Using the Basic proportionality theorem, we have
\(\frac{P E}{E Q}=\frac{P D}{D O}\) …………… (1)
Again, in ∆POR, DF || OR [given]
∴ Using the Basic proportionality theorem, we have
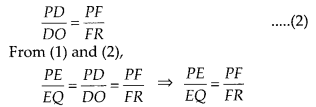
Now, in ∆PQR,
∵ E and F are two distinct points on PQ and PR respectively and \(\frac{P E}{E Q}=\frac{P F}{F R}\),
i.e., E and F divide the two sides PQ and PR of ∆PQR in the same ratio.
∴ By converse of Basic proportionality theorem, EF || QR.
Question 6.
In the figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
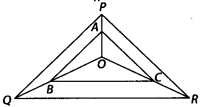
Solution:
In ∆PQR, O is a point and OP, OQ and OR are joined. We have points A, B and C on OP, OQ and OR respectively such that AB || PQ and AC || PR.
Now, in ∆OPQ,
∵ AB || PQ [Given]
Using the Basic proportionality theorem, we have

i.e., B and C divide the sides OQ and OR of ∆OQR in the same ratio.
By converse of Basic proportionality theorem, BC || QR.
![]()
Question 7.
Using Basic proportionality theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. A
Solution:
We have ∆ABC, in which D is the midpoint of AB and E is a point on AC such that DE || BC.
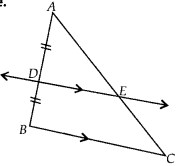
∵ DE || BC [given]
∴ Using the Basic proportionality theorem, we get

⇒ E is the mid point of AC. Hence, it is proved that a line through the midpoint of one side of a triangle parallel to another side bisects the third side.
Question 8.
Using converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:
We have ∆ABC, in which D and E are the mid-points of sides AB and AC respectively.
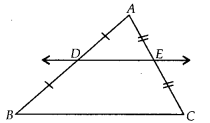
∴ AD = DB ……………. (1)
and AE = EC ………….. (2)
From (1) and (2), we have
\(\frac{A D}{D B}\) = 1 and \(\frac{A E}{E C}\) = 1
⇒ \(\frac{A D}{D B}=\frac{A E}{E C}\)
⇒ DE || BC (By converse proportionality theorem).
![]()
Question 9.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}=\frac{C O}{D O}\).
Solution:
We have, a trapezium ABCD such that AB || DC. The diagonals AC and BD intersect each other at O.
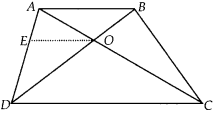
Let us draw OE parallel to either AB or DC.
In ∆ADC
OE || DC [By construction]
∴ Using the Basic proportionality theorem, we get
\(\frac{A E}{E D}=\frac{A O}{C O}\) …………. (1)
In ∆ABD
OE || AB [By construction]
∴ Using the Basic proportionality theorem, we get
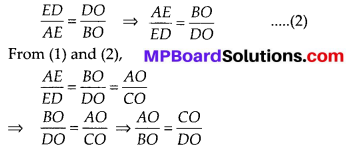
Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{A O}{B O}=\frac{C O}{D O}\). Show that ABCD is a trapezium.
Solution:
It is given that \(\frac{A O}{B O}=\frac{C O}{D O}\)
From \(\frac{A O}{B O}=\frac{C O}{D O}\), we have \(\frac{A O}{C O}=\frac{B O}{D O}\)
Let us draw OE such that OE || BA
In ∆ADB, OE || AB [By construction]
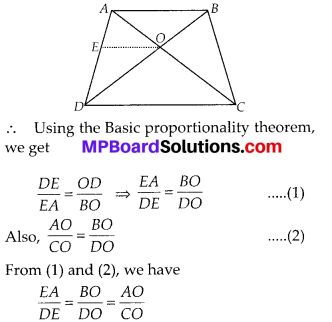
i.e., the points O and E divide the sides AC and AD of ∆ADC respectively in the same ratio.
∴ Using the converse of Basic proportionality theorem, we get OE || DC and OE || AB
⇒ AB || DC
⇒ ABCD is a trapezium.