MP Board Class 10th Maths Solutions Chapter 5 समान्तर श्रेढ़ियाँ Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 5 समान्तर श्रेढ़ियाँ Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 5 समान्तर श्रेढ़ियाँ Additional Questions

MP Board Class 10th Maths Chapter 5 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 5 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी AP के प्रथम पाँच पदों का योग और उसी श्रेणी के प्रथम सात पदों का योग का कुल योग 167 है। यदि उस श्रेणी के प्रथम 10 पदों का योग 235 हो, तो उस श्रेणी के प्रथम 20 पदों का योग ज्ञात कीजिए।
हल :
माना AP का प्रथम पद a एवं सार्वान्तर d है, तो प्रश्नानुसार,
S₅ + S₇ = \(\frac { 5 }{ 2 }\)[2a + 4d] + \(\frac { 7 }{ 2 }\)[2a + 6d] = 167
\(\frac{10 a+20 d}{2}+\frac{14 a+42 d}{2}=167\)
\(\frac{24 a+62 d}{2}\) = 167 ⇒ 12a + 31d = 167 …(1)
S₁₀ = \(\frac { 10 }{ 2 }\)[2a + 9d] = 235
2a + 9d = 47 …(2)
12a + 54d = 282 ….(3) [समीकरण (2) x 6 से]
23d = 115 [समीकरण (3) – समीकरण (1) से]
d = \(\frac { 115 }{ 23 }\) = 5
d का मान समीकरण (2) में रखने पर,
2a + 9 x 5 = 47
2a = 47 – 45 = 2
a = \(\frac { 2 }{ 2 }=1\)
S_n = \(\frac { n }{ 2 }\)[2a + (n – 1) d]
S₂₀ = \(\frac { 20 }{ 2 }\)[2 x 1+ (20 – 1) x 5]
= 10[2 + 95]
= 10 x 97
= 970
अतः प्रथम 20 पदों का अभीष्ट योग = 970 है।

प्रश्न 2.
निम्न को ज्ञात कीजिए:
(i) 1 से 500 के मध्य उन पूर्णाकों का योग जो 2 और 5 से विभाज्य हैं।
(ii) 1 से 500 तक उन पूर्णाकों का योग जो 2 एवं 5 से विभाज्य हैं।
हल :
(i) 1 और 500 के मध्य 2 एवं 5 से विभाज्य अर्थात् 10 से विभाज्य पूर्णांक होंगे क्रमशः
10, 20, 30, 40, ……………., 480, 490.
जहाँ a = 10, d = 20 – 10 = 10 एवं a_n = 490
a_n = a + (n – 1) x d
10 + (n – 1) x 10 = 490
10 + 10n – 10 = 490
n = \(\frac { 490 }{ 10 }=49\) पद
S_n = \(\frac { n }{ 2 }\)[2a + (n-1) x d]
S₄₉ = \(\frac { 49 }{ 2 }\)[2 x 10 + (49-1) – 10]
= \(\frac { 49 }{ 2 }\)[20 + 480]
= \(\frac { 49 }{ 2 }\) x 500
= 12250
अतः अभीष्ट योग = 12250 है।

(ii) 1 से 500 तक की 2 एवं 5 से विभाज्य अर्थात् 10 से विभाज्य संख्याएँ क्रमश: 10, 20, 30, ……………, 490, 500 होंगी, जो एक AP का निर्माण करती हैं,
जहाँ a = 10, d = 20 – 10 = 10 एवं a_n = 500.
a_n = a + (n-1) x d
10 + (n-1) x 10 = 500
10 + 10n – 10 = 500
n = \(\frac { 500 }{ 10 }\) = 50
S_n = \(\frac { n }{ 2 }\)[2a + (n-1) x d]
S₅₀ = \(\frac { 50 }{ 2 }\)[2 x 10 + (50 – 1) x 10]
S₅₀ = 25[20 + 490]
= 25 x 510
= 12750
अंत: अभीष्ट योग = 12750 है।

प्रश्न 3.
किसी AP का 8वाँ पद इसके दूसरे पद का आधा है एवं 11वाँ पद इसके 4वें पद के एक-तिहाई से एक अधिक है। इसके 15वें पद को ज्ञात कीजिए।
हल :
मान लीजिए AP का प्रथम पद a एवं सार्वान्तर d है, तो प्रश्नानुसार,
a₈ = \(\frac { 1 }{ 2 }\)a₂
⇒ a + 7d = \(\frac { 1 }{ 2 }\)(a + d)
2a + 14d = a + d
⇒ a + 13d= 0 ….(1)
a₁₁ = \(\frac { 1 }{ 3 }\)a₄ + 1
a + 10d = \(\frac { 1 }{ 3 }\)(a + 3d) + 1
3a + 30d = a + 3d + 3
2a + 27d = 3
2a + 26d = 0 …(3) [समीकरण (1) x 2 से]
d = 3 [समीकरण (2) – समीकरण (3) से]
अब d का मान समीकरण (1) में रखने पर,
a + 13 x 3 = 0
a_n = – 13 x 3 = – 39
a = a + (n – 1) x d
a₁₅ = – 39 + (15 – 1) x 3
a₁₅ = – 39 + 42 = 3
अत: अभीष्ट 15वाँ पद = 3 है।

प्रश्न 4.
100 और 200 के मध्य उन पूर्णांकों का योग ज्ञात कीजिए जो
(i) 9 से विभाज्य है,
(i)9 से विभाज्य नहीं है।
हल :
(i) 100 एवं 200 के मध्य 9 से विभाज्य पूर्णांक हैं : 108, 117, 126, ……., 189, 198. जो एक AP का निर्माण करते हैं, जहाँ a = 108,d = 117 – 108 = 9 एवं a_n = 198
a_n = a+ (n-1) x d
198 = 108 + (n-1) x 9 = 108 + 9n – 9
9n = 198 + 9 – 108 = 207 – 108 = 99
n = \(\frac { 99 }{ 9 }\) = 11
अब चूँकि S_n = \(\frac { n }{ 2 }\)[2a + (n-1) x d]
S₁₁ = \(\frac { 11 }{ 2 }\)[2 x 108 + (11-1) x 9]
= \(\frac { 11 }{ 2 }\)[216 + 90]
= \(\frac { 11 }{ 2 }\) x 306
S₁₁ = 11 x 153
= 1683
अतः 100 और 200 के मध्य 9 से विभाज्य संख्याओं का अभीष्ट योग = 1683 है।

(ii) 100 और 200 के मध्य पूर्णांक क्रमशः 101, 102, 103, …………, 199 होंगे, जो एक AP का निर्माण करते हैं, जहाँ a = 101 एवं d = 102 – 101 = 1 तथा a_n = 199.
a_n = a + (n-1) x d
199 = 101 + (n – 1) x 1 = 101 + n-1 = n + 100
n = 199 – 100 = 99
S_n = \(\frac { n }{ 2 }\)[2a + (n-1) x d]
S₉₉ = \(\frac { 99 }{ 2 }\)[2 x 101+ (99 -1) x 1]
= \(\frac { 99 }{ 2 }\)[202 + 98]
= \(\frac { 99 }{ 2 }\) x 300
= 99 x 150
= 14850
चूँकि 100 और 200 के मध्य 9 से अविभाज्य संख्याओं का योग
= 100 और 200 के मध्य सभी संख्याओं का योग – 100 और 200 के मध्य 9 से विभाज्य संख्याओं का योग।
अभीष्ट योग = 14850 – 1683 = 13167
अतः 100 और 200 के मध्य 9 से अविभाज्य संख्याओं का योग = 13167 है।

प्रश्न 5.
एक AP के 11वें पद का 18वें पद से अनुपात 2 : 3 है। 5वें पद का 21वें पद से अनुपात ज्ञात कीजिए और साथ ही प्रथम पाँच पदों के योग का प्रथम 21 पदों के योग से अनुपात ज्ञात कीजिए।
हल :
मान लीजिए AP का प्रथम पद a तथा सार्वान्तर d है, तो प्रश्नानुसार,

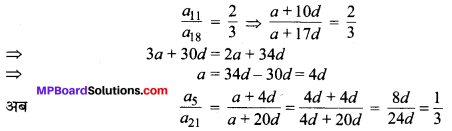
अतः a₅ : a₂₁ का अभीष्ट अनुपात 1 : 3 है।

अत: S₅ : S₂₁ का अभीष्ट अनुपात 5 : 49 है।

प्रश्न 6.
एक समान्तर श्रेढ़ी का 14वाँ पद उसके 8वें पद का दुगना है। यदि उसका छटा पद – 8 है, तो उसके प्रथम 20 पदों का योगफल ज्ञात कीजिए।
हल :
मान लीजिए AP का प्रथम पद a एवं सार्वान्तर d है, तो प्रश्नानुसार
a + 13d = 2(a + 7d)
= 2a + 14d
⇒ a + d = 0 …(1)
⇒ a + 5d = -8 …(2)
⇒ 4d = – 8 [समीकरण (2) – समीकरण (1) से]
⇒ d = \(-\frac { 8 }{ 4 }\) = -2
⇒ a + (-2) = 0 [d का मान समीकरण (1) में रखने पर]
⇒ a = 2
⇒ S_n = \(\frac { n }{ 2 }\)[2a + (n-1)d]
⇒ S₂₀ = \(\frac { 20 }{ 2 }\)[2 x 2 + (20 – 1) (-2)]
= 10 (4 – 38)
= 10 (-34)
= – 340
अतः AP के प्रथम 20 पदों का अभीष्ट योग = – 340 है।

प्रश्न 7.
समान्तर श्रेढ़ी 8, 10, 12, ……………. का 60वाँ पद ज्ञात कीजिए। यदि उसमें कुल 60 पद हैं, तो इस श्रेढ़ी के अन्तिम दस पदों का योगफल ज्ञात कीजिए।
हल :
दी हुई AP 8, 10, 12, ………….. T_n में ज्ञात है,
प्रथम पद a = 8 एवं सार्वान्तर d = 10 – 8 = 2 तथा n = 60 है।
∴ T_n = a + (n – 1)d
T₆₀ = 8 + (60 – 1) x 2
= 8 + 59 x 2
= 8 + 118
= 126
अत: अभीष्ट 60वाँ पद = 126 है।
अब श्रेढ़ी को उल्टे क्रम में लिखने पर,
AP = 126, 124, 122, ……… होगी।।
जिसका प्रथम पद a’ = 126 एवं सार्वान्तर d’ = 124 – 126 = – 2 एवं n’ = 10 है।
S_n’ = \(\frac { n’ }{ 2 }\)[2a’ + (n’ – 1) x d’]
S₁₀ = \(\frac { 10 }{ 2 }\)[2 x 126 + (10 – 1) – (-2)]
S₁₀ = 5[252 + 9(-2)]
= 5[252 – 18]
= 5 x 234
= 1170
अतः श्रेणी के अन्तिम दस पदों का अभीष्ट योग = 1170 है।

प्रश्न 8.
यदि दो समान्तर श्रेढ़ियों के प्रथम n पदों के योगों में (7n + 1) : (4n + 27) का अनुपात है, तो उनके mवे पदों में अनुपात ज्ञात कीजिए।
हल :
मान लीजिए कि दी गई समान्तर श्रेढ़ियाँ हैं :
a₁, a₁ + d₁, a₁ + 2d₁, + ……….
एवं a₂, a₂ + d₂, a₂ + 2d₂ + ……….
तो प्रश्नानुसार,

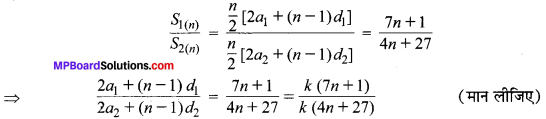
2a₁ + nd₁ – d₁ = 7k n + k
d₁ n + 2a₁ – d₁ = 7k n + k
d₁ = 7k एवं 2a₁ – d₁ = k
[स्थिरांक एवं n के गुणांकों की तुलना करने पर]
2a₁ – 7k = k ⇒ 2a₁ = 8k ⇒ a₁ = \(\frac { 8k }{ 2 }\) = 4k
2a₂ + nd₂ – d₂ = 4k n + 27k
d₂n + 2a₂ – d₂ = 4kn + 27k
d₂ = 4k एवं 2a₂ – d₂ = 27k
स्थिरांक एवं n के गुणांकों की तुलना करने पर]
2a₂ – 4k = 27k
⇒ 2a₂ = 31k
⇒ a₂ = \(\frac { 31 }{ 2 }\) k

अतः उनके mवें पदों का अभीष्ट अनुपात = \(\frac { 14m-6 }{ 8m+23 }\) है।

प्रश्न 9.
यदि दो समान्तर श्रेढ़ियों के n पदों के योगफलों का अनुपात (7n + 1) : (4n + 27) है, तो उनके 9वें पदों का अनुपात ज्ञात कीजिए।
हल :
(m = 9 लेकर उपर्युक्त प्रश्न की तरह हल करें।)
[उत्तर – अभीष्ट अनुपात = \(\frac { 24 }{ 19 }\)]

प्रश्न 10.
एक समान्तर श्रेढ़ी के प्रथम पदों के योगफल को S_n द्वारा प्रदर्शित किया जाता है। इस श्रेढ़ी में यदि S₅ + S₇ = 167 तथा S₁₀ = 235 है, तो समान्तर श्रेढ़ी ज्ञात कीजिए।
हल :
[निर्देश : दीर्घ उत्तरीय प्रश्न 1 का हल देखिए जिसमें हम a = 1 एवं d= 5 प्राप्त करते हैं।
चूँकि a = 1 एवं d = 5 तो
a₁ = a = 1
a₂ = a + d = 1 + 5 = 6
a₃ = a + 2d = 1 + 5 x 2 = 1 + 10 = 11
a₄ = a + 3d = 1 + 3 + 5 = 1 + 15 = 16
…………………………
………………………..
a_n = a+ (n – 1)d = 1 + (n – 1) x 5
= 1 + 5n – 5 = 5n – 4
अत: अभीष्ट समान्तर श्रेढी 1, 6, 11, 16, …. 5n – 4 हैं।

MP Board Class 10th Maths Chapter 5 लघु उत्तरीय प्रश्न

प्रश्न 1.
पुष्टि कीजिए कि निम्न में प्रत्येक AP है तब अगले तीन-तीन पद लिखिए :
(i) \(0, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\)……..
(ii) \(5, \frac{14}{3}, \frac{13}{3}, 4\)…………
(iii) √3, 2√3, 3√3……
(iv) a + b, (a + 1) + b, (a +1) + (b + 1), ………
(v) a, 2a + 1, 3a + 2, 4a + 3,………
हल :
(i) \(0, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}\)……..
चूँकि यहाँ

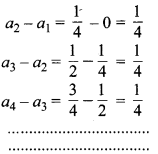
सार्वान्तर समान है अतः AP है।
अब अगले तीन पद

अत: अभीष्ट अगले तीन \(1, \frac{5}{4}, \frac{3}{2}\) हैं।

(ii) \(5, \frac{14}{3}, \frac{13}{3}, 4\)…………
चूँकि यहाँ

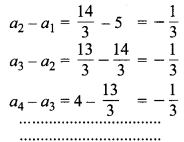
सार्वान्तर समान हैं अत: AP है।
अब अगले तीन पद क्रमशः हैं

अतः अभीष्ट अगले तीन पद \(\frac{11}{3}, \frac{10}{3}\) एवं 3 हैं।

(iii) √3, 2√3, 3√3, ……
चूँकि यहाँ a₂ – a₁ = 2 √3 – √3 = √3
एवं a₃ – a₂ = 3 √3 – 2 √3 = 3
सार्वान्तर समान हैं अतः AP है।
अब अगले तीन पद क्रमशः हैं
(3√3 + √3 = 4√3), (4√3 + √3 = 5√3) एवं (5√3 + √3 = 6√3)
अत: अभीष्ट अगले तीन पद 4√3, 5√3, एवं 6√3 हैं।

(iv) a+ b, (a + 1)+ b, (a + 1) + (b + 1), ……
चूँकि यहाँ
a₂ – a₁ = [(a + 1) + b] – (a + b) = 1
a₃ – a₂ = [(a + 1) + (b + 1)] – [(a + 1) + (b)] = 1
………….
………….
सार्वान्तर समान है अत: AP है।
अब अगले तीन पद क्रमशः
(a + 1) + (b + 1) + 1 = (a + 2) + (b + 1)
(a + 2) + (b + 1) + 1 = (a + 2) + (b + 2)
(a + 2) + (b + 2)+ 1 = (a + 3) + (b + 2)
………
………
अतः अभीष्ट अगले तीन पद क्रमशः (a + 2) + (b + 1), (a + 2) + (b + 2) एवं (a + 3)+ (b + 2) हैं।

(v) a, 2a + 1, 3a + 2, 4a + 3, …..
चूँकि यहाँ
a₂ – a₁ = (2a + 1) – a = a+ 1
a₃ – a₂ = (3a + 2) – (2a + 1) = a + 1
एवं a₄ – a₃ = (4a + 3) – (3a + 2) = a + 1
……………
……………
सार्वान्तर समान है अत: AP है।
अब अगले तीन पद क्रमशः
(4a + 3) + (a + 1) = (5a + 4)
(5a + 4) + (a + 1) = (6a + 5)
(6a + 5) + (a + 1) = (7a + 6)
अत: अभीष्ट अगले तीन पद क्रमशः (5a + 4), (6a + 5) एवं (7a + 6) हैं।

प्रश्न 2.
उन AP के प्रथम तीन पद लिखिए जिनके a एवं d नीचे दिए गए हैं :
(i) a = \(\frac { 1 }{ 2 }\), d = \(-\frac { 1 }{ 6 }\)
(ii) a = -5, d = -3
(iii) a = √2, d = \(\frac{1}{\sqrt{2}}\)
हल :
(i) यहाँ a = \(\frac { 1 }{ 2 }\), एवं d = \(-\frac { 1 }{ 6 }\) (दिया है)


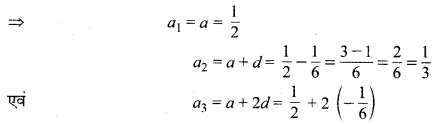
अतः अभीष्ट प्रथम तीन पद क्रमशः \(\frac{1}{2}, \frac{1}{3}\) एवं \(\frac { 1 }{ 6 }\) हैं।

(ii) चूँकि यहाँ a = – 5 एवं d= – 3 (दिया है)
a₁ = a = -5
a₂ = a + d = (-5) + (-3) = – 5 – 3 = -8
a₃ = a + 2d = (-5) + 2 (-3) = – 5 – 6 = – 11
अतः अभीष्ट प्रथम तीन पद क्रमशः – 5, -8 एवं -11 हैं।

(iii) चूँकि यहाँ a = √2 एवं d = \(\frac{1}{\sqrt{2}}\) (दिया है)

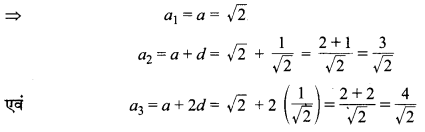
अतः अभीष्ट प्रथम तीन पद क्रमशः \(\sqrt{2}, \frac{3}{\sqrt{2}}\) एवं \(\frac{4}{\sqrt{2}}\) हैं।

प्रश्न 3.
a, b एवं c के मान ज्ञात कीजिए जिसमें कि a, 7, b, 13 एवं c एक AP में हों।
हल :
चूँकि a, 7, b, 23 एवं c एक AP में हैं और मान लीजिए प्रथम पद a तथा सार्वान्तर d हो, तो
a₁ = a = a …(1)
a₂ = a + d = 7 …..(2)
a₃ = a + 2d = b ….(3)
a₄ = a + 3d = 23 …(4)
a₅ = a + 4d = c …….(5)
(a + 3d) – (a + d) = 23 – 7 [समी. (4) – समी. (2) से]
⇒ 2d = 16
⇒ d = \(\frac { 16 }{ 2 }\) = 8
d = 8 का मान समीकरण (2) में रखने पर,
a + 8 = 7 ⇒ a = 7 – 8 = -1
अब b = a + 2d = – 1 + 2 x 8 = – 1 + 16 = 15
एवं c = a + 4d = – 1 + 4 x 8 = – 1 + 32 = 31
अतः a, b एवं c के अभीष्ट मान क्रमशः – 1, 15 एवं 31 हैं।

प्रश्न 4.
ज्ञात कीजिए कि 55 दी हुई AP 7, 10, 13,……. का कोई पद है या नहीं। अगर है तो ज्ञात कीजिए यह कौन-सा पद है?
हल :
AP : 7, 10, 13, …….. (दी है)
यहाँ a = 7 एवं d = 10 – 7 = 3
मान लीजिए 55 इस AP का nवाँ पद है
a_n = a + (n – 1)d
55 = 7 + (n – 1) x 3 = 7 + 3n – 3
3n = 55 + 3 – 7 = 58 – 7 = 51
n = \(\frac { 51 }{ 3 }\) = 17
अतः 55 दी हुई AP का 17वाँ पद है।

प्रश्न 5.
निम्न AP का योग ज्ञात कीजिए :
(i) 1 + (-2) + (-5) + (-8) + ……….. + (-236)
(ii) \(\left(4-\frac{1}{n}\right)+\left(4-\frac{2}{n}\right)+\left(4-\frac{3}{n}\right)+\) …. n पदों तक
(iii) \(\frac{a-b}{a+b}+\frac{3 a-2 b}{a+b}+\frac{5 a-3 b}{a+b}+\)………11 पदों तक
हल :
(i) 1 + (-2) + (-5) + (-8) + ……. + (-236).
यहाँ a = 1 एवं d = (-2) – (1) = – 3 एवं a_n = – 236
a_n = a + (n – 1) x d
– 236 = 1 + (n – 1) (-3)
– 236 = 1 – 3n + 3
3n = 236 + 1 + 3 = 240
n = \(\frac { 240 }{ 3 }\) = 80
S_n = \(\frac { n }{ 2 }\)[a + a]
S₈₀ = \(\frac { 80 }{ 2 }\) [1+ (-236)]
= 40 (-235)
= – 9400
अतः अभीष्ट योग = – 9400 है।

(ii) \(\left(4-\frac{1}{n}\right)+\left(4-\frac{2}{n}\right)+\left(4-\frac{3}{n}\right)+\) …. n पदों तक

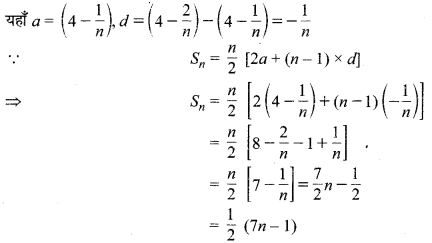
अत: अभीष्ट योग = \(\frac { 1 }{ 2 }\) (7n – 1) है।

(iii) \(\frac{a-b}{a+b}+\frac{3 a-2 b}{a+b}+\frac{5 a-3 b}{a+b}+\)………11 पदों तक


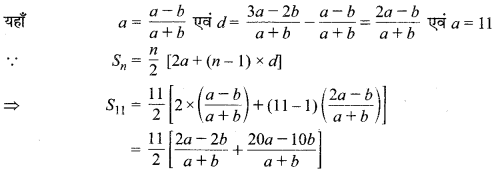
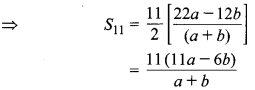
अत: अभीष्ट योग = \(\frac { 11(11a-6b) }{ a+b }\) है।

प्रश्न 6.
AP: -2, -7, -12, ……. का कौन-सा पद – 77 है। इस AP का पद – 77 तक योग ज्ञात कीजिए।
हल :
यहाँ a = – 2, d = (-7) – (-2) = -7 + 2 = – 5 एवं a_n = – 77
a_n = a + (n – 1) x d
– 77 = – 2 + (n – 1)(-5)= – 2 – 5n + 5
5n = 77 + 5 – 2 = 82 – 2 = 80
n = \(\frac { 80 }{ 2 }\) = 16
अतः – 77 दी हुई AP का 16वाँ पद है।
अब ∵ S_n = \(\frac { n }{ 2 }\)[a + a_n]
S₁₆ = \(\frac { 16 }{ 2 }\)[-2 – 77]
= 8 (-79)
= – 632
अतः अभीष्ट योग = -632 है।

प्रश्न 7.
यदि a_n = 3 – 4n तो दर्शाइए कि a₁, a₂, a₃, ………. एक AP का निर्माण करते हैं। S₂₀ का मान भी ज्ञात कीजिए।
हल :
चूंकि a_n = 3 – 4n
a₁ = 3 – 4 x 1 = 3 – 4 = – 1
a₂ = 3 – 4 x 2 = 3 – 8 = – 5
a₃ = 3 – 4 x 3 = 3 – 12 = – 9
…………….
…………….
a₁, a₂, a₃, ……… =- 1, -5,-9, ……….
एवं a₂ – a₁ = (-5) – (-1) = – 5 + 1 = – 4
a₃ – a₂ = (-9) – (-5) = -9 + 5 = – 4
चूँकि यहाँ सार्वान्तर d = -4 समान है
अत: a₁, a₂, a₃, ……. एक AP का निर्माण करते हैं।
अब ∵ S_n = \(\frac { n }{ 2 }\)[2a + (n – 1) x d]
S₂₀ = \(\frac { 20 }{ 2 }\)[2 (-1) + (20 – 1) – (-4)]
= 10 [-2 – 76]
= 10 (-78)
= – 780
अतः S₂₀ का अभीष्ट मान = – 780 है।

प्रश्न 8.
एक समान्तर श्रेढ़ी का प्रथम पद 5, अंतिम पद 45 तथा इसके सभी पदों का योगफल 400 है। इस समान्तर श्रेढ़ी के पदों की संख्या तथा सार्वान्तर ज्ञात कीजिए।
हल :
दी हुई समान्तर श्रेढ़ी का प्रथम पद a = 5 तथा अन्तिम पद T_n = 45, योगफल S_n = 400 दिए हैं। मान लीजिए सार्वान्तर d है तो प्रश्नानुसार,
∵ S_n = \(\frac { n }{ 2 }\) [a + T_n]
400 = \(\frac { n }{ 2 }\) [5 + 45]
⇒ 25n = 400
n = \(\frac { 400 }{ 25 }\) = 16
T_n = a + (n – 1) x d
45 = 5 + (16 – 1) x d
15d = 40
d = \(\frac{40}{15}=\frac{8}{3}\)
अतः पदों की अभीष्ट संख्या = 16 एवं सार्वान्तर = \(\frac { 8 }{ 3 }\) है।

प्रश्न 9.
श्रेढ़ी \(20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4}\)….. का कौन-सा पद प्रथम ऋणात्मक पद हैं?
हल :
दी हुई समान्तर श्रेढ़ी का प्रथम पद a = 20
तथा सार्वान्तर d = \(19\frac { 1 }{ 4 }\) – 20 = \(-\frac { 3 }{ 4 }\) है।
मान लीजिए nवाँ पद प्रथम ऋणात्मक पद है।
T_n = a + (n – 1)d
\(20+(n-1) \times\left(-\frac{3}{4}\right)<0\)
80 + 3 – 3n < 0
3n > 83
n > \(\frac { 83 }{ 3 }\)
n > \(27\frac { 2 }{ 3 }\)
n = 28
अतः अभीष्ट प्रथम ऋणात्मक पद = 28वाँ पद है।

प्रश्न 10.
एक समान्तर श्रेढ़ी का चौथा पद शून्य है। सिद्ध कीजिए कि इसका 25वाँ पद उसके 11वें पद का तीन गुना है।
हल :
मान लीजिए किसी समान्तर श्रेढ़ी का प्रथम पद a तथा सार्वान्तर d है तो प्रश्नानुसार,
T₄ = a + 3d = 0
⇒ a = -3d ……(1)
अब
⇒ \(\frac{T_{25}}{T_{11}}=\frac{a+24 d}{a+10 d}\) …….(2)
समीकरण (1) से a = – 3d मान समीकरण (2) में रखने पर,
\(\frac{T_{25}}{T_{11}}=\frac{-3 d+24 d}{-3 d+10 d}=\frac{21 d}{7 d}=3\)
T₂₅ = 3 x T₁₁
अतः दी हुई श्रेढ़ी का 25वाँ पद उसके 11वें पद का तीन गुना है।
इति सिद्धम्

MP Board Class 10th Maths Chapter 5 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्न में से कौन-कौन AP बनाते हैं? अपने उत्तर की पुष्टि कीजिए।
(i)-1,-1,-1,-1, …………..
(ii) 0, 2, 0, 2, ………….
(iii) 1, 1, 2, 2, 3, 3, ……….
(iv) 11, 22, 33, …….
(v) \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\)…..
(vi) 2,2²,2³,2⁴,………..
(vii) √3, √12, √27, √48,…………..
हल :
(i)- 1, – 1, – 1, – 1, ……..
चूँकि a₂ – a₁ = (-1) – (-1) = 0
एवं a₃ – a₂ = (-1) – (-1) = 0
a₄ – a₃ = (-1) – (-1) = 0
a₂ – a₁ = a₃ – a₂ = 0
अतः उक्त श्रेढ़ी एक AP है।

(ii) 0, 2, 0, 2, ….
चूँकि a₂ – a₁ = 2 – 0 = 2
एवं a₃ – a₂ = 0 – 2 = – 2
a₂ – a₁ ≠ a₃ – a₂
अतः उक्त श्रृंखला एक AP नहीं है।

(iii) 1, 1, 2, 2, 3, 3, …………
चूँकि a₂ – a₁ = 1 – 1 = 0
एवं a₃ – a₂ = 2 – 1 = 1
a₂ – a₁ ≠ a₃ – a₂
अतः उक्त श्रृंखला एक AP नहीं है।

(iv) 11, 22, 33, ….
चूँकि a₂ – a₁ = 22 – 11 = 11
एवं a₃ – a₂ = 33 – 22 = 11
a₂ – a₁ = a₃ – a₂ = 11
अतः उक्त श्रृंखला एक AP है।

(v) \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\)…..

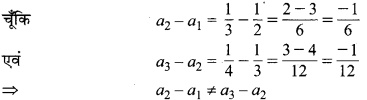
अतः उक्त श्रृंखला एक AP नहीं है।

(vi) 2, 2², 2³, 2⁴,…….
चूँकि a₂ – a₁ = 2² – 2 = 4 – 2 = 2
एवं a₃ – a₂ = 2³ – 2² = 8 – 4 = 4
a₂ – a₁ ≠ a₃ – a₂
अतः उक्त श्रृंखला एक AP नहीं है।

(vii) √3, √12, √27, √48,…………..
अर्थात् √3, 2√3, 3√3, 4√3,……..
चूँकि a₂ – a₁ = 2√3 – √3 = √3
एवं a₃ – a₂ = 3√3 – 2√3 = √3
a₂ – a₁ = a₃ – a₂ = √3
अतः उक्त श्रृंखला एक AP है।

प्रश्न 2.
पुष्टि कीजिए कि यह कहना सत्य है कि \(-1, \frac{-3}{2},-2, \frac{5}{2}\) …… एक AP बनाती है। क्योंकि a₂ – a₁ = a₃ – a₂.
हल :
शृंखला \(-1, \frac{-3}{2},-2, \frac{5}{2}\) ……
चूँकि

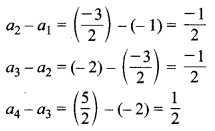
चूँकि (a₃ – a₂) ≠ (a₄ – a₃)
अतः यह कहना गलत है कि उक्त श्रृंखला एक AP है।

प्रश्न 3.
एक AP -3,-7,-11,………. है। क्या हम बिना a₂₀ एवं a₃₀ ज्ञात किए हुए a₃₀ – a₂₀ का मान ज्ञात कर सकते हैं। अपने उत्तर का कारण दीजिए।
हल :
∵ a₃₀ = a + 29d
एवं a₂₀ = a + 19d
a₃₀ – a₂₀ = (a + 29d) – (a + 19d) = 10d
चूँकि यहाँ d = (-7) – (-3)
= -7 + 3
= -4
a₃₀ – a₂₀ = 10d = 10 (-4)
= -40
हाँ हम बिना a₂₀ एवं a₃₀ ज्ञात किए a₃₀ – a₂₀ ज्ञात कर सकते हैं जैसा कि ऊपर दिखाया गया है।

प्रश्न 4.
क्या AP: 31, 28, 25, …….. का कोई पद है 0 ? अपने उत्तर की पुष्टि कीजिए।
हल :
AP : 31, 28, 25, ……….
जहाँ a = 31 एवं d = 28 – 31 = -3
मान लीजिए 0 इस AP का nवाँ पद है।
a_n = a + (n-1) x d
0 = 31 + (n – 1) x (-3)
0 = 31 – 3n + 3
3n = 31 + 3 = 34
n = \(\frac { 34 }{ 3 }\) जो एक पूर्णांक नहीं है
अतः 0 दी गई AP का कोई पद नहीं है।

प्रश्न 5.
इस बात की पुष्टि कीजिए कि “क्या यह कहना सत्य है कि निम्नांकित पद किसी AP के nवें पद हैं।”
(i) 2n – 3
(ii) 3n² + 5
(iii) 1 + n + n²
हल :
(i) यदि
a_n = 2n – 3
a₁ = 2 x 1 – 3 = 2 – 3 = -1
a₂ = 2 x 2 – 3 = 4 – 3 = 1
a₃ = 2 x 3 – 3 = 6 – 3 = 3
a₂ – a₁ = 1 – (-1) = 1 + 1 = 2
a₃ – a₂ = 3 – 1 = 2
a₂ – a₁ = a₃ – a₂ = 2
अतः उक्त पद एक AP का nवाँ पद है।

(ii) यदि
a_n = 3n² + 5
a₁ = 3 (1)² + 5 = 3 + 5 = 8
a₂ = 3 (2)² + 5 = 12 + 5 = 17
a₃ = 3 (3)² + 5 = 27 + 5 = 32
a₂ – a₁ = 17 – 8 = 9 एवं a₃ – a₂ = 32 – 17 = 15
a₂ – a₁ ≠ a₃ – a₂
अतः उक्त पद किसी AP का nवाँ पद नहीं है।

(iii) यदि
a_n = 1 + n + n²
a₁ = 1+ 1 + (1)² = 1 + 1 + 1 = 3
a₂ = 1 + 2 + (2)² = 1 + 2 + 4 = 7
a₃ = 1 + 3 + (3)² = 1 + 3 + 9 = 13
a₂ – a₁ = 7 – 3 = 4 एवं a₃ – a₂ = 13 – 7 = 6
a₂ – a₁ ≠ a₃ – a₂
अतः उक्त पद किसी AP का nवाँ पद नहीं है।

प्रश्न 6.
k के किस मान के लिए k + 9, 2k – 1 तथा 2k + 7 एक समान्तर श्रेढ़ी के क्रमागत पद हैं?
हल :
चूँकि k + 9, 2k – 1 तथा 2k + 7 एक समान्तर श्रेढ़ी के क्रमागत पद हैं।
⇒ (2k – 1) – (k + 9) = (2k + 7) – (2k – 1)
⇒ 2k – 1 – k – 9 = 2k + 7 – 2k + 1
⇒ k = 10 + 8 = 18
अतःk का अभीष्ट मान = 18 है।

प्रश्न 7.
एक समान्तर श्रेढ़ी जिसमें a₂₁ – a₇ = 84 है का सार्वान्तर क्या है?
हल :
मान लीजिए श्रेढ़ी का प्रथम पद a तथा सार्वान्तर d है
a₂₁ – a₇ = 84 (दिया है)
⇒ (a + 20a) – (a + 6d) = 84
⇒ 20d – 6d = 84
⇒ 14d = 84
⇒ d = \(\frac { 84 }{ 14 }\) = 6
अतः अभीष्ट सार्वान्तर = 6 है।

MP Board Class 10th Maths Chapter 5 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 5 बहु-विकल्पीय प्रश्न

प्रश्न 1.
किसी AP में यदि d = -4,n = 7 एवं a_n = 4 तो a है :
(a) 6
(b) 8
(c) 20
(d) 28.
उत्तर:
(d) 28.

प्रश्न 2.
किसी AP में यदि a = 3.5, d = 0,n = 101, तब a_n का मान होगा :
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5.
उत्तर:
(b) 3.5

प्रश्न 3.
संख्याओं की सूची -10, -6, – 2, 2, ……….. है :
(a) एक AP, जहाँ d = – 16
(b) एक AP, जहाँ d = 4
(c) एक AP, जहाँ d = – 4
(d) एक AP नहीं।
उत्तर:
(b) एक AP, जहाँ d = 4

प्रश्न 4.
एक AP: \(-5, \frac{-5}{2}, 0, \frac{5}{2}\) ,………. का 11वाँ पद होगा :
(a) – 20
(b) 20
(c) – 30
(d) 30.
उत्तर:
(b) 20

प्रश्न 5.
एक AP का प्रथम पद -2 और सार्वान्तर – 2 है के प्रथम चार पद होंगे :
(a) – 2, 0, 2, 4
(b) – 2, 4, – 8, 16
(c) – 2, – 4, – 6, – 8
(d) – 2, – 4, – 8, – 16.
उत्तर:
(c) – 2, – 4, – 6, – 8

प्रश्न 6.
किसी AP के प्रथम दो पद – 3 एवं 4 हैं, इसका 21वाँ पद होगा :
(a) 17
(b) 137
(c) 143
(d) – 143.
उत्तर:
(b) 137

प्रश्न 7.
एक AP का दूसरा पद 13 है तथा इसका पाँचवाँ पद 25 है तो इसका 7वाँ पद क्या होगा?
(a) 30
(b) 33
(c) 37
(d) 38.
उत्तर:
(b) 33

प्रश्न 8.
किसी AP: 21, 42, 63 84,………. का कौन-सा पद 210 होगा?
(a) 9वाँ
(b) 10वाँ
(c) 11वाँ
(d) 12वाँ।
उत्तर:
(b) 10वाँ

प्रश्न 9.
यदि एक AP का सार्वान्तर 5 है तब a₁₈ – a₁₃ का क्या मान होगा?
(a) 5
(b) 20
(c) 25
(d) 30.
उत्तर:
(c) 25

प्रश्न 10.
उस AP का सार्वान्तर क्या होगा जिसमें a₁₈ – a₁₄ = 32 ?
(a) 8
(b) -8
(c) -4
(d) 4.
उत्तर:
(a) 8

प्रश्न 11.
दो AP का सार्वान्तर समान है। एक AP का प्रथम पद 1 एवं दूसरी का प्रथम पद 8 तब उनके चौथे पदों में अन्तर होगा:
(a) -1
(b) -8
(c) 7
(d) -9.
उत्तर:
(c) 7

प्रश्न 12.
एक AP के 7वें पद का 7 गुना उसके 11वें पद के 11 गुने के बराबर है तब इसका 18वाँ पद है:
(a) 7
(b) 11
(c) 18
(d) 0.
उत्तर:
(d) 0.

प्रश्न 13.
किसी AP :- 11,-8,-5,……….49 के अन्त से चौथा पद है :
(a) 37
(b) 40
(c) 43
(d) 58.
उत्तर:
(b) 40

प्रश्न 14.
प्रथम 100 प्राकृत संख्याओं का योग ज्ञात करने वाले प्रसिद्ध गणितज्ञ थे :
(a) पाइथगोरस
(b) न्यूटन
(c) गॉउस
(d) यूक्लिड।
उत्तर:
(c) गॉउस

प्रश्न 15.
एक AP का प्रथम पद – 5 है तथा सार्वान्तर 2 है तब प्रथम 6 पदों का योग है :
(a) 0
(b) 5
(c) 6
(d) 15.
उत्तर:
(a) 0

प्रश्न 16.
एक AP : 10, 6, 2, ……….. के प्रथम 16 पदों का योग है :
(a) – 320
(b) 320
(c) – 352
(d)- 400.
उत्तर:
(a) – 320

प्रश्न 17.
एक AP में a = 1, a_n = 20 एवं S_n = 399 तब n का मान है :
(a) 19
(b) 21
(c) 38
(d) 42.
उत्तर:
(c) 38

प्रश्न 18.
3 के प्रथम पाँच गुणकों का योग है :
(a) 45
(b) 55
(c) 65
(d) 75.
उत्तर:
(a) 45

प्रश्न 19.
AP: 5, 8, 11, 14,……… का 10वाँ पद है:
(a) 32
(b) 35
(c) 38
(d) 185.
उत्तर:
(a) 32

प्रश्न 20.
किसी AP में यदि a = 7.2, d = 3.6 एवं a_n = -7.2 तब n का मान है :
(a) 1
(b) 3
(c) 4
(d) 5.
उत्तर:
(d) 5.

रिक्त स्थानों की पूर्ति

1. जब किसी अनुक्रम के पदों को किसी नियम द्वारा लिखा जाता है, तो इसे ………. कहते हैं।
2. वह अनुक्रम जिसका प्रत्येक पद अपने पूर्ववर्ती पद से एक निश्चित अन्तर रखता है ………. कहलाता है।
3. समान्तर श्रेढ़ी के किसी पद का उसके पूर्ववर्ती पद में अन्तर ………… कहलाता है।
4. कोई तीन राशियाँ समान्तर श्रेढ़ी में हों तो मध्य वाली राशि शेष दो राशियों का ……….. कहलाती है।
5. एक समान्तर श्रेढ़ी का प्रथम पद a तथा सार्वान्तर d हो तो उसका nवाँ पद ………… होगा।
6. सार्वान्तर श्रेढ़ी \(\frac{3}{2}, \frac{1}{2},-\frac{1}{2},-\frac{3}{2}, \ldots\) सार्वान्तर d = ………. है। (2019)
उत्तर-
1. श्रेढ़ी,
2. समान्तर श्रेढ़ी,
3. सार्वान्तर,
4. समान्तर माध्य,
5. a + (n – 1)d,
6. – 1.

जोड़ी मिलाइए

उत्तर-
1.→(c),
2.→(d),
3.→(e),
4.→(a),
5.→(b).

सत्य/असत्य कथन

1. समान्तर श्रेढ़ी के पद सदैव बढ़ते क्रम में होते हैं।
2. 5 और 7 का समान्तर माध्य 6 होता है।
3. समान्तर श्रेढ़ी के किन्हीं दो पदों का अन्तर सार्वान्तर होता है।
4. समान्तर श्रेढ़ी 10, 5, ………. का अगला पद 0 होगा।
5. 1, 2, 1, 3, ………… एक समान्तर श्रेढ़ी है।
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर

1. 2√2, √2 , 0, ……….. का अगला पद क्या होगा?
2. 5, 10, 15, ……… का अगला पद क्या होगा?
3 \(\frac{3}{\sqrt{5}}, \frac{4}{\sqrt{5}}, \sqrt{5}\) ……….. कौन-सी श्रेढ़ी है?
4. \(\frac{1}{4}, \frac{1}{3}, \frac{1}{4}\) ……….. समान्तर श्रेढ़ी है या नहीं?
5. यदि किसी श्रेढ़ी में पदों की संख्या सीमित न हो तो उसे क्या कहते हैं?
उत्तर-
1. -√2 ,
2. 20,
3. समान्तर श्रेढ़ी,
4. नहीं,
5. अनन्त श्रेढ़ी।