In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.3 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.3
प्रश्न 1.
निम्न रैखिक समीकरण युग्मों को प्रतिस्थापन विधि से हल कीजिए :
(i) x + y = 14; x – y = 4
(ii) s – t = 3; \(\frac { s }{ 3 } \) + \(\frac { t }{ 2 } \) = 6
(iii) 3x – y = 3; 9x – 3y = 9
(iv) 0.2x + 0.3y = 1.33; 0.4x + 0.5y = 2.3
(v) \(\sqrt { 2 }\) x + \(\sqrt { 3 }\) y = 0; \(\sqrt { 3 }\) x – \(\sqrt { 8 }\) y = 0
(vi) \(\frac { 3x }{ 2 } \) – \(\frac { 5y }{ 3 } \) = -2; \(\frac { x }{ 3 } \) + \(\frac { y }{ 2 } \) = \(\frac { 13 }{ 6 } \)
हल:
(i) चूँकि
x + y = 14 ….(1)
एवं x – y = 4 ….(2)
समीकरण (2) से x का मान x = y + 4 समीकरण (1) में प्रतिस्थापित करने पर हम पाते हैं :
y + 4 + y = 14 ⇒ 2y = 10 ⇒ y = \(\frac { 10 }{ 2 } \) = 5
एवं x = y + 4 = 5 + 4 = 9
अतः दत्त समीकरण युग्म का अभीष्ट हल x = 9 एवं y = 5 है।
(ii) चूँकि s – t = 3 ….(1)
एवं \(\frac { s }{ 3 } \) + \(\frac { t }{ 2 } \) = 6 ….(2)
समीकरण (1) से s = t + 3 समीकरण (2) में प्रतिस्थापित करने पर हम पाते हैं :
\(\frac { t+3 }{ 3 } \) + \(\frac { t }{ 2 } \) = 6 ⇒ 2t + 6 + 3t = 36
⇒ 5 t = 30 ⇒ t = \(\frac { 30 }{ 5 } \) = 6
एवं s = t + 3 = 6 + 3 = 9
अतः दत्त समीकरण युग्म का अभीष्ट हल s = 9 एवं t = 6 है।
(iii) चूँकि 3x – y = 3
एवं 9x – 3y = 9
समीकरण (1) से y = 3x – 3 समीकरण (2) में प्रतिस्थापित करने पर हम पाते हैं :
9x – 3 (3x – 3) = 9 ⇒ 9x – 9x + 9 = 9
⇒ 9 = 9 जो x से रहित समीकरण है
इसलिए x के सभी मानों के लिए सत्य है।
अतः उक्त समीकरण युग्म के अभीष्ट हल अनन्तशः अनेक हैं :
(iv) चूंकि 0.2x + 0.3y = 1.3 ….(1)
एवं 0.4x + 0.5y = 2.3 ….(2)
⇒ 2x + 3y = 13 ….(3)
[दोनों समीकरणों को 10 से गुणा करने पर]
एवं 4x + 5y = 23
समीकरण (3) से x = \(\frac { 13-3y }{ 2 } \) समीकरण (4) में प्रतिस्थापित करने पर हम पाते हैं:
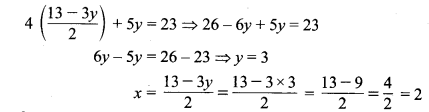
अतः उक्त समीकरण युग्म का अभीष्ट हल x = 2 एवं y = 3 है।
(v) चूँकि \(\sqrt { 2 }\)x + \(\sqrt { 3 }\) y = 0 …(1)
एवं \(\sqrt { 3 }\)x – \(\sqrt { 8 }\) y = 0 ….(2)
समीकरण (1) से x = \(=\frac{-\sqrt{3}}{\sqrt{2}}\) करण (2) में प्रतिस्थापित करने पर हम पाते हैं:
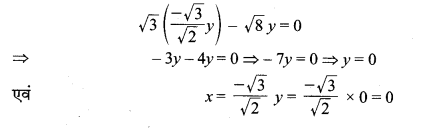
अतः उक्त समीकरण युग्म का अभीष्ट हल x = 0 एवं y = 0 है।
(vi) चूँकि \(\frac { 3x }{ 2 } \) – \(\frac { 5y }{ 3 } \) = -2 ….(1)
एवं \(\frac { x }{ 3 } \) + \(\frac { y }{ 2 } \) = \(\frac { 13 }{ 6 } \) ….(2)
⇒ 9x – 10y = -12 ….(3)
[दोनों समीकरणों को 6 से गुणा करने पर]
एवं 2x + 3y = 13 ….(4)
समीकरण (4) से, x = \(\frac { 13-3y }{ 2 } \) समीकरण (3) में प्रतिस्थापित करने पर हम पाते हैं:
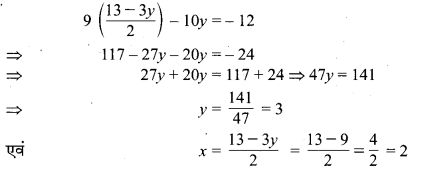
अतः उक्त समीकरण युग्म का अभीष्ट हल x = 2 एवं y = 3 है।
![]()
प्रश्न 2.
2x + 3y = 11 और 2x – 4y = -24 को हल कीजिए और इससे ‘m’ का वह मान ज्ञात कीजिए जिसके लिए y = mx + 3 हो।
हल:
चूँकि 2x + 3y = 11 ….(1)
एवं 2x – 4y = – 24 ….(2)
समीकरण (2) से x = 2y – 12 समीकरण (1) में प्रतिस्थापित करने पर हम पाते हैं:
2 (2y – 12) + 3y = 11 ⇒ 4y – 24 + 3y = 11
⇒ 7y = 11 + 24 = 35 ⇒ y = \(\frac { 35 }{ 7 } \) = 5
एवं x = 2y – 12 = 2 × 5 – 12 = 10 – 12 = -2
अत: दत्त समीकरणों का अभीष्ट हल x = -2 एवं y = 5 है।
अब चूँकि y = mx + 3
⇒ 5 = m (-2) + 3 (x एवं y के मान रखने पर)
⇒ 2 m = 3 – 5 = -2 ⇒ m = \(\frac { -2 }{ 2 } \) = -1
अत: m का अभीष्ट मान = -1 है।
![]()
प्रश्न 3.
निम्न समस्याओं में रैखिक समीकरण युग्म बनाइए और उनके हल प्रतिस्थापन विधि द्वारा ज्ञात कीजिए :
(i) दो संख्याओं का अन्तर 26 है और एक संख्या दूसरी संख्या की तीन गुनी है। उन्हें ज्ञात कीजिए।
(ii) दो सम्पूरक कणों में बड़ा कोण छोटे कोण से 18 डिग्री अधिक है। उन्हें ज्ञात कीजिए।
(iii) एक क्रिकेट टीम के कोच ने 7 बल्ले तथा 6 गेंदें ₹ 3800 में खरीदीं। बाद में उसने 3 बल्ले तथा 5 गेंदें ₹ 1750 में खरीदीं। प्रत्येक बल्ले एवं प्रत्येक गेंद का मूल्य ज्ञात कीजिए।
(iv) एक नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 10 km दूरी के लिए भाड़ा ₹ 105 है, तथा 15 km दूरी के लिए भाड़ा ₹ 155 है। नियत भाड़ा तथा प्रति km भाड़ा क्या है? एक व्यक्ति को 25 km यात्रा करने के लिए कितना भाड़ा देना होगा?
(v) यदि किसी भिन्न के अंश और हर दोनों में 2 जोड़ दिया जाए, तो वह ” हो जाती है। यदि अंश और हर दोनों में 3 जोड़ दिया जाए तो वह – हो जाती है। वह भिन्न ज्ञात कीजिए।
(vi) पाँच वर्ष बाद जैकब की आयु उसके पुत्र की आयु से तीन गुनी हो जाएगी। पाँच वर्ष पूर्व जैकब की आयु उसके पुत्र की आयु से सात गुनी थी। उनकी वर्तमान आयु क्या है?
हल:
(i) मान लीजिए अभीष्ट संख्याएँ x एवं y हैं और x > y तो प्रश्नानुसार,
x – y = 26 …(1) एवं x = 3y …(2)
अब समीकरण (2) सेx का मान समीकरण (1) में प्रतिस्थापित करने पर हम पाते हैं:
3y – y = 26 ⇒ 2y = 26 ⇒ y = \(\frac { 26 }{ 2 } \) = 13
एवं x = 3y = 3 × 13 = 39
अतः अभीष्ट संख्याएँ क्रमशः 39 एवं 13 हैं।
(ii) मान लीजिए कि दो अभीष्ट सम्पूरक कोण x एवं y हैं और x > y तो प्रश्नानुसार,
x + y = 180 ….(1) (सम्पूरक कोणों का योग = 180°)
एवं x – y = 18 ….(2)
समीकरण (2) से x = 18 + y समीकरण (1) में रखने पर हम पाते हैं :
18 + y + y = 180 ⇒ 2y = 180 – 18 = 162
⇒ y = \(\frac { 162 }{ 2 } \) = 81
एवं x = 18 + y = 18 + 81 = 99
अतः अभीष्ट कोण क्रमश: 99° एवं 81° हैं।
(iii) मान लीजिए एक बल्ले का मूल्य ₹x एवं एक गेंद का मूल्य ₹y है तो प्रश्नानुसार,
7x + 6y = 3800 …..(1)
एवं 3x + 5y = 1750 …..(2)
समीकरण (2) से x = \(\frac { 1750-5y }{ 3 } \) समीकरण (1) में रखने पर,
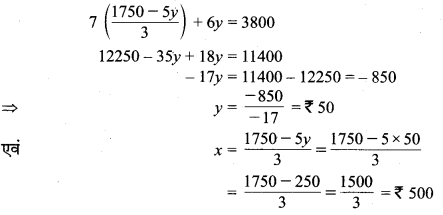
अतः बल्ले एवं गेंद का अभीष्ट मूल्य क्रमशः ₹ 500 एवं ₹50 प्रति नग हैं।
(iv) मान लीजिए कि नियत भाड़ा ₹ x एवं प्रति km भाड़े की दर ₹ y है, तो प्रश्नानुसार,
x + 10y = 105 ….(1)
एवं x + 15y = 155 ….(2)
अब समीकरण (1) से x = 105 – 10y समीकरण (2) में प्रतिस्थापित करने पर,
105 – 10y + 15y = 155 ⇒ 10y + 15y = 155 – 105
⇒ 5y = 50 ⇒ y = \(\frac { 50 }{ 5 } \) = ₹ 10
एवं x = 105 – 10y = 105 – 10 × 10 = 105 – 100 = ₹5
अतः अभीष्ट नियत भाड़ा ₹ 5 एवं प्रति km भाड़े की दर ₹10 है।
(v) मान लीजिए कि भिन्न का अभीष्ट अंश x एवं हर y है, तो अभीष्ट भिन्न = \(\frac { x }{ y } \) है।
अब प्रश्नानुसार, \(\frac { x+2 }{ y+2 } \) = \(\frac { 9 }{ 11 } \)
⇒ 11x + 22 = 9y + 18
⇒ 11x – 9y = 18 – 22 = – 4 ….(1)
एवं \(\frac { x+3 }{ y+3 } \) = \(\frac { 5 }{ 6 } \)
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = 15 – 18 = -3
समीकरण (2) से x = \(\frac { 5y-3 }{ 6 } \) समीकरण (1) में प्रतिस्थापित करने पर हम पाते हैं :
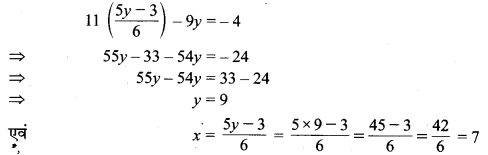
(vi) मान लीजिए जैकब की वर्तमान आयु x वर्ष एवं उसके पुत्र की वर्तमान आयु y वर्ष है
तो प्रश्नानुसार, (x + 5) = 3 (y + 5)
⇒ x – 3y = 15 – 5 = 10 ….(1)
एवं (x – 5) = 7 (y – 5)
⇒ x – 7y = – 35 + 5 = -30 ….(2)
समीकरण (2) से x = 7y – 30 समीकरण (1) में प्रतिस्थापित करने पर हम पाते हैं :
7y – 30 – 3y = 10
⇒ 7y – 3y = 10 + 30.
⇒ 4y = 40 ⇒ y = \(\frac { 40 }{ 4 } \) = 10 वर्ष
एवं x = 7y – 30 = 7 × 10 – 30 = 70 – 30 = 40 वर्ष
अतः जैकब की अभीष्ट वर्तमान आयु = 40 वर्ष एवं उसके पुत्र की वर्तमान आयु = 10 वर्ष