In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.1 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter दो चरों वाले रैखिक समीकरण युग्म Ex 3.1
प्रश्न 1.
आफताब अपनी पुत्री से कहता है, “सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गुनी आयु का रह जाऊँगा।” (क्या यह मनोरंजक है?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
हल:
मान लीजिए कि आफताब एवं उसकी पुत्री की वर्तमान आयु क्रमशः x वर्ष और y वर्ष है, तो
प्रश्नानुसार,
(x – 7) = 7 (y – 7)
⇒ x – 7 = 7y – 49
⇒ x – 7y + 42 = 0 …(1)
एवं (x + 3)= 3 (y + 3)
⇒ x + 3 = 3y + 9
⇒ x – 3y – 6 = 0 …(2)
यह स्थिति मनोरंजक भी हैतथा गणितीय तथ्यपरक है। इस स्थिति का बीजगणितीय निरूपण है।
x – 7y + 42 = 0 एवं x – 3y – 6 = 0
ग्राफीय निरूपण के लिए :
∵ x – 7y + 42 = 0 ….(1)
⇒ y = \(\frac { 42+x }{ 7 } \)

चूँकि x – 3y – 6 = 0 ….(2)
⇒ y = \(\frac { x-6 }{ 3 } \)
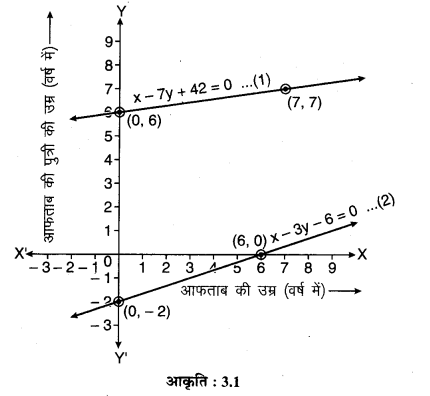
उपर्युक्त आकृति अभीष्ट ग्राफीय निरूपण है।
![]()
प्रश्न 2.
क्रिकेट टीम के एक कोच ने ₹ 3900 में 3 बल्ले तथा 6 गेंदें खरीदी। बाद में उसने एक और बल्ला तथा उसी प्रकार की 3 गेंदें ₹ 1300 में खरीदीं। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
हल:
माना 1 बल्ले एवं 1 गेंद का मूल्य क्रमशः ₹ x तथा ₹ y है।
तो प्रश्नानुसार, 3x + 6y = 3900
⇒ x + 2y = 1300
एवं x + 3y = 1300 अतः दी गई स्थितियों का बीजगणितीय निरूपण है:
x + 2y = 1300 …(1) एवं x + 3y = 1300 …(2)
जहाँ x एवं y क्रमशः 1 बल्ले और 1 गेंद के मूल्य (₹ में) हैं।
ज्ञातव्य – उपर्युक्त स्थितियाँ व्यावहारिक रूप से अनुपयुक्त हैं। ये तभी सम्भव हो सकती हैं जबकि प्रत्येक गेंद मुफ्त में मिल रही हो अथवा मूल्य में परिवर्तन हुआ हो।
ज्यामितीय (ग्राफीय) निरूपण के लिएः
चूँकि x + 2y = 1300 ….(1)
⇒ y = \(\frac { 1300-x }{ 2 } \)
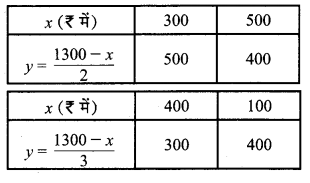
एवं x + 3y = 1300 ….(2)
⇒ y = \(\frac { 1300-x }{ 3 } \)
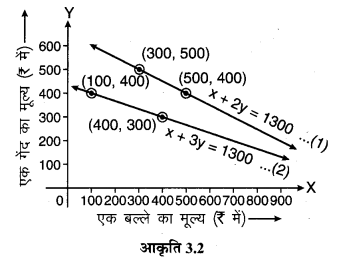
अतः उपर्युक्त आकृति दी गई स्थितियों का ज्यामितीय (ग्राफीय) निरूपण है।
![]()
प्रश्न 3.
2 kg सेब और 1 kg अंगूर का मूल्य किसी दिन ₹ 160 था। एक महीने बाद 4 kg सेब और 2 kg अंगूर का मूल्य ₹ 300 हो जाता है। इस स्थिति को बीजगणितीय तथा ज्यामितीय रूपों में व्यक्त कीजिए।
हल:
मान लीजिए कि 1 किलो सेब एवं 1 किलो अंगूर का मूल्य क्रमश: ₹ x एवं ₹ y है।
तो प्रश्नानुसार, 2x + y = 160 ….(1)
एवं 4x + 2y = 300
⇒ 2x + y = 150 ….(2)
अतः दी गई स्थितियों का बीजगणितीय निरूपण है:
2x + y = 160 ..(1) 2x + y = 150 …(2)
ज्यामितीय (ग्राफीय) निरूपण के लिए:
चूँकि 2x + y = 160 ….(1)
⇒ y = 160 – 2x
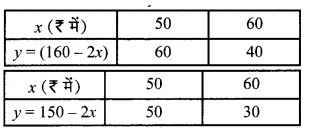
एवं 2x + y = 150 ….(2)
⇒ y = 150 – 2x
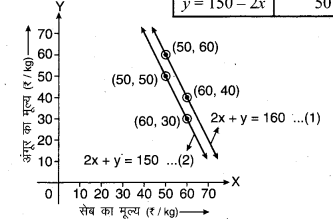
आकृति 3.3
अतः उपर्युक्त आकृति दी गई स्थितियों का ज्यामितीय (ग्राफीय) निरूपण है।