In this article, we will share MP Board Class 10th Maths Book Solutions Pair of Linear Equations in Two Variables Ex 3.1 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 3Pair of Linear Equations in Two Variables Ex 3.1
Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. (Isn’t this interesting?) Represent this situation algebraically and graphically.
Solution:
At present: Let Aftab’s age = x years
His daughter’s age = y years
Seven years ago : Aftab’s age = (x – 7) years
His daughter’s age = (y – 7)years
According to the condition,
[Aftab’s age] = 7[His daughter’s age]
⇒ [x – 7] = 7[y – 7] = x – 7 = 7y – 49
⇒ x – 7y – 7 + 49 = 0 ⇒ x – 7y + 42 = 0 …. (1)
After three years : Aftab’s age = (x + 3) years
His daughter’s age = (y + 3) years
According to the condition,
[Aftab’s age] = 3[His daughter’s age]
⇒ [x + 3] = 3[y + 3]
⇒ x + 3 = 3y + 9 ⇒ x — 3y + 3 — 9 = 0
⇒ x — 3y – 6 = 0 …. (2)
Graphical representation of equation (1) and (2): From equation (1), we have :

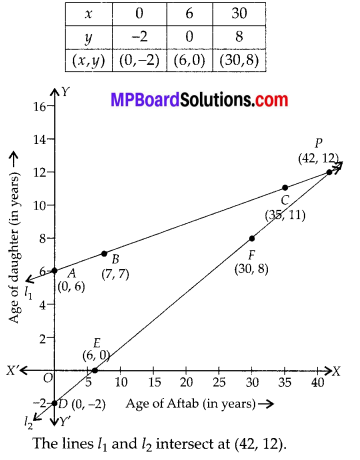
Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let the cost of a bat = ₹ x
and the cost of a ball = ₹ y
Cost of 3 bats = ₹ 3x
and cost of 6 balls = ₹ 6y
Again, cost of 1 bat = ₹ x
and cost of 3 balls = ₹ 3y
Algebraic representation:
Cost of 3 bats + Cost of 6 balls = ₹ 3900
⇒ 3x + 6y = 3900 ⇒ x + 2y = 1300 …. (1)
Also, cost of 1 bat + cost of 3 balls = ₹ 1300
⇒ x + 3y = 1300 …. (2)
Thus, (1) and (2) are the algebraic representations of the given situation.
Geometrical representation:
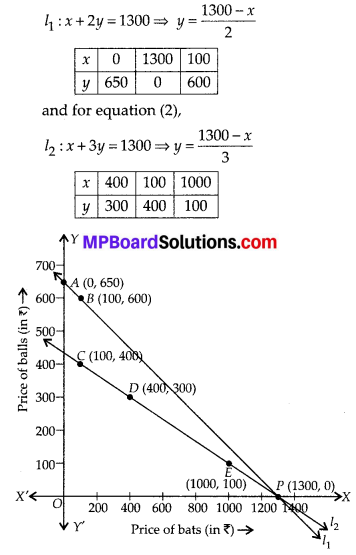
We have for equation (1),
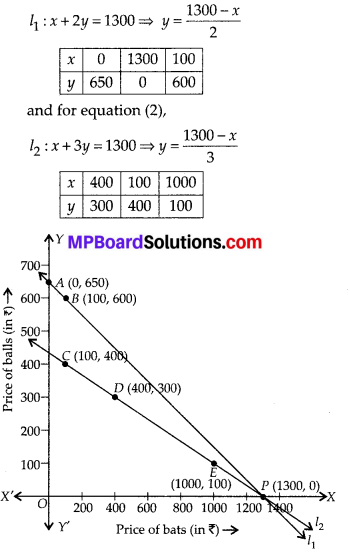
We can also see from the obtained graph that the straight lines representing the two equations intersect at (1300, 0).
![]()
Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.
solution:
Let the cost of 1 kg of apples = ₹ x
And the cost of 1 kg of grapes = ₹ y
Algebraic representation:
2x + y = 160 … (1)
and 4x + 2y = 300
⇒ 2x + y = 150 … (2)
Geometrical representation:
We have, for equation (1),
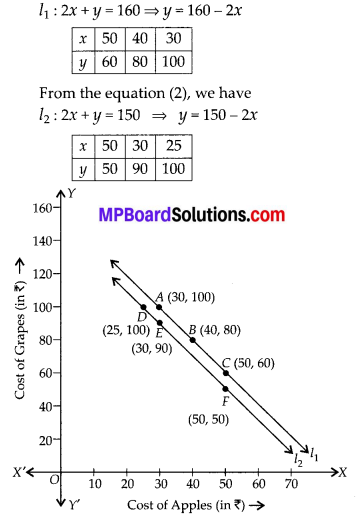
The straight lines l1 and l2 are the geometrical representations of the equations (1) and (2) respectively. The lines are parallel.