In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 15 प्रायिकता Ex 15.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 15 प्रायिकता Ex 15.2
(नोट : यह प्रश्नावली परीक्षा की दृष्टि से नहीं है।)
प्रश्न 1.
दो ग्राहक श्याम और एकता एक विशेष दुकान पर ही एक सप्ताह में जा रहे हैं (मंगलवार से शनिवार तक)। प्रत्येक द्वारा दुकान पर किसी दिन या किसी अन्य दिन जाने के परिणाम समप्रायिक हैं। इसकी क्या प्रायिकता है कि दोनों उस दुकान पर
(i) एक ही दिन जाएँगे?
(ii) क्रमागत दिनों में जाएँगे?
(iii) भिन्न दिनों में जाएँगे?
हल :
कुल दिनों की संख्या = 5 (मंगलवार से शनिवार) श्याम दुकान पर 5 तरह से जा सकता है तथा इसी प्रकार एकता भी दुकान पर 5 प्रकार से जा सकती है।
∴ कुल सम्भाव्य स्थितियाँ = n(S) = 5 x 5 = 25
(i) एक ही दिन जाने की अनुकूल स्थितियाँ = (मंगल, मंगल), (बुध, बुध), (बृह., बृह.) (शुक्र, शुक), (शनि, नि)
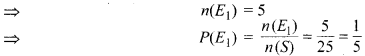
(ii) वे दोनों क्रमागत दिनों में निम्न 8 प्रकार से जा सकते हैं : (मं., बु.), (बु., बृ.), (बृ., शु.), (शु., श.), (बु., मं.), (बृ., बु.), (शु., बृ.), (श., शु.)
∴ क्रमागत दिनों में जाने की अनूकूलता
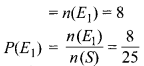
(iii) भिन्न-भिन्न दिनों में जाएँगे = एक ही दिन नहीं जाएँगे
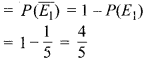
अतः अभीष्ट प्रायिकताएँ : (i) \(\frac { 1 }{ 5 }\), (ii) \(\frac { 8 }{ 25 }\), (iii) \(\frac { 4 }{ 5 }\) है।
प्रश्न 2.
एक पासे के फलकों पर संख्याएँ 1, 2, 2, 3, 3 और 6 लिखी हुई हैं। इसे दो बार फेंका जाता है तथा दोनों बार प्राप्त हुई संख्याओं के योग लिख लिए जाते हैं। दोनों बार फेंकने के बाद प्राप्त योग के सम्भावित कुछ मान निम्नलिखित सारणी में दिए हैं। इस सारणी को पूरा कीजिए :
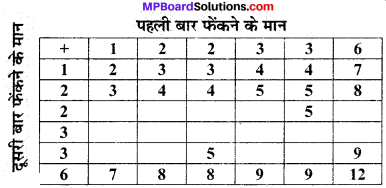
इसकी क्या प्रायिकता है कि कुल योग
(i) एक सम संख्या होगा?
(ii) 6 है?
(iii) कम-से-कम 6 है?
हल :
सारणी को पूरा करने पर अभीष्ट सारणी है :
(i) योग सम संख्या के अनुकूल परिणाम
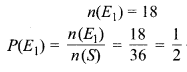
(ii) योग 6 के अनुकूल परिणामों की संख्या
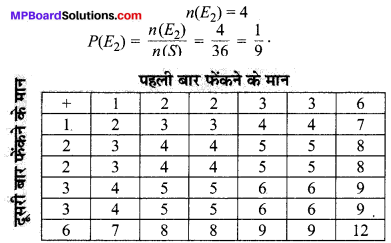
(iii) योग कम-से-कम 6 के अनुकूल परिणामों की संख्या
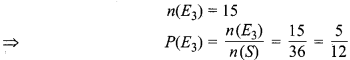
अतः अभीष्ट प्रायिकताएँ : (i) \(\frac { 1 }{ 2 }\), (ii) \(\frac { 1 }{ 9 }\) एवं \(\frac { 5 }{ 12 }\) हैं।
![]()
प्रश्न 3.
एक थैले में 5 लाल गेंद और कुछ नीली गेंदें हैं। यदि इस थैले में से नीली गेंद निकालने की प्रायिकता लाल गेंद निकालने की प्रायिकता की दुगनी है, तो थैले में नीली गेंदों की संख्या ज्ञात कीजिए।
हल :
मान लीजिए थैले में नीली गेंदो की संख्या = x है।
चूँकि लाल गेंदों के अनुकूल परिणामों की संख्या
= n(ER) = 5
एवं नीली गेंदों के अनुकूल परिणामों की संख्या
= n(EB) = x है।
तो प्रश्नानुसार,
नीली गेंद निकालने की प्रायिकता P(EB) = 2 x लाल गेंद निकालने की प्रायिकता P(EB)
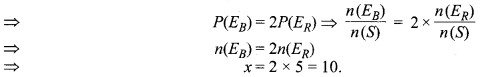
अतः नीली गेंदों की अभीष्ट संख्या = 10 है।
प्रश्न 4.
एक पेटी में 12 गेंदें हैं, जिनमें से x गेंदें काली हैं। यदि इनमें से एक गेंद यादृच्छया निकाली जाती है, तो इसकी प्रायिकता ज्ञात कीजिए कि यह काली है। यदि इस पेटी में 6 काली गेंदें और डाल दी जायें, तो काली गेंद निकालने की प्रायिकता पहली प्रायिकता की दुगनी हो जाती है। x का मान ज्ञात कीजिए।
हल :
कुल सम्भावित घटनाओं के परिणामों की संख्या = n(S) = 12.
काली गेंदें निकलने की अनुकूल परिणामों की संख्या n(E) = x.
⇒ \(P\left(E_{1}\right)=\frac{n\left(E_{1}\right)}{n(S)}=\frac{x}{12}\) ….(i)
6 काली गेंदें और मिलाने पर कुल सम्भावित घटनाओं के परिणामों की संख्या = n(S) = 12 + 6 = 18.
अब काली गेंद निकलने के अनुकूल परिणामों की नयी संख्या = n(E) = x + 6.
⇒ \(P\left(E_{2}\right)=\frac{n\left(E_{2}\right)}{n\left(S_{2}\right)}=\frac{x+6}{18}\) …(ii)
प्रश्नानुसार,
⇒ P(E2) = 2 x P(E1)
⇒ \(\frac{x+6}{18}=2 \times \frac{x}{12}\)
⇒ 36x = 12x + 72
⇒ 36x – 12x = 72
⇒ 24x = 72
⇒ x = \(\frac { 72 }{ 24 }\) = 3
अतः, x का अभीष्ट मान = 3 है।
![]()
प्रश्न 5.
एक जार में 24 कंचे हैं जिनमें कुछ हरे हैं और शेष नीले हैं। यदि इस जार में से यादृच्छया एक कंचा निकाला जाता है, तो इस कंचे के हरा होने की प्रायिकता \(\frac { 2 }{ 3 }\) है। जार में नीले कंचों की संख्या ज्ञात कीजिए।
हल :
मान लीजिए कि नीले कंचों की संख्या x है
हरे कंचों की संख्या = (24 – x)
हरे कंचे के निकलने के अनुकूल परिणामों की संख्या = n(E) = (24 – x)
एवं कुल सम्भावित परिणामों की संख्या n(S) = 24
![]()
⇒ 48 = 72 – 3x
⇒ 3x = 72 – 48 = 24
⇒ x = \(\frac { 24 }{ 3 }\) = 8
अतः, नीले कंचों की अभीष्ट संख्या = 8 है।