In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5
ज्ञातव्य – यह प्रश्नावली परीक्षा की दृष्टि से नहीं है।
प्रश्न 1.
व्यास 3 mm वाले ताँबे के एक तार को 12 cm लम्बे और 10 cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्रपृष्ठ को पूर्णतया ढक लेता है। तार की लम्बाई और द्रव्यमान ज्ञात कीजिए, यह मानते हुए कि ताँबे का घनत्व 8.88 g प्रति cm³ है।
हल :
मान लीजिए बेलन की ऊँचाई h = 12 cm एवं व्यास D = 10 cm तथा तार का व्यास d = 2r = 3 mm = 0.3 cm ⇒ r = 0.15 cm
चूँकि बेलन का वक्रपृष्ठ = πDh = 3.14 x 10 x 12 cm²
Sc = 376.8 cm²
मान लीजिए तार की लम्बाई l है, जो बेलन को पूर्णतया ढक लेती है।
![]()
अतः, तार की अभीष्ट लम्बाई = 1256 cm है।
चूँकि तार का आयतन = πr²l
⇒ V = 3.14 x (0.15)² x 1256
ताँबे का आयतन V = 88.74 cm³
ताँबे का घनत्व = 8.88 g/cm³ (दिया है)
चूँकि तार का द्रव्यमान = तार का आयतन x ताँबे का घनत्व
⇒ M = 88.74 x 8.88
= 788 g (लगभग)
अतः, ताँबे का अभीष्ट द्रव्यमान = 788 g (लगभग) है।
प्रश्न 2.
एक समकोण त्रिभुज जिसकी भुजाएँ 3 cm और 4 cm हैं (कर्ण के अतिरिक्त) को उसके कर्ण के परितः घुमाया जाता है। इस प्रकार प्राप्त द्वि शंकु (double cone) के आयतन एवं पृष्ठीय क्षेत्रफल ज्ञात कीजिए (π का मान जो भी उपयुक्त लगे प्रयोग कीजिए)।
हल :
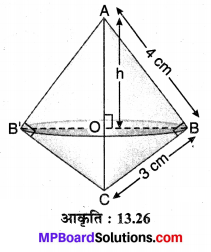
मान लीजिए कि ∆ABC एक समकोण ∆ है जिसमें AB = 4cm एवं BC = 3 cm दिए हैं तथा ∆ABC को कर्ण AC के परितः घुमाया गया है जिसमें दो शंकु प्राप्त होते हैं।
मान लीजिए AO = h cm
(देखिए संलग्न आकृति)
समकोण ∆ABC में, \(A C=\sqrt{A B^{2}+B C^{2}}\)
(पाइथागोरस प्रमेय से)
\(A C=\sqrt{(4)^{2}+(3)^{2}}=\sqrt{16+9}\)
= √25
= 5 cm
चूँकि AO = h माना गया है। OC = (5 – h) cm
चूँकि ₹ABCB’ के ∠ABC + ∠AB’C = 180°
⇒ चतुर्भुज ABCB’ एक चक्रीय चतुर्भुज है, जिसकी जीवा AC, जीवा BB’ का लम्ब समद्विभाजक हैं।
[ ∆AB’B एक समद्विबाहु ∆ है तथा AC शीर्ष लम्ब है।]
OB’ = OB = r (मान लीजिए)
OB’ x OB = AO x OC
⇒ r² = h x (5 – h) ….(1)
समकोण ∆AOB में पाइथागोरस प्रमेय से,
OB² = AB² – AO²
r² = (4)² – (h)² ….(2)
एवं समकोण ∆BOC में पाइथागोरस प्रमेय से,
OB² = BC² – OC²
r² = (3)² – (5 – h)² …(3)
⇒ (3)² – (5 – h)² = (4)² – (h)²
[समीकरण (2) एवं (3) से]
⇒ 9 – (25 – 10h + h²) = 16 – h²
⇒ 9 – 25 + 10h – h² = 16 – h²
⇒ 10h = 16 + 25 – 9 = 32
⇒ h = \(\frac { 32 }{ 10 }\) = 3.2 cm
⇒ h² = (4)² – (3.2)²
= 16 – 10.24
= 5.76 ….(4)
⇒ r = √5.76
= 2.4 cm
चूँकि द्विशंकु का आयतन

एवं द्विशंकु का पृष्ठीय क्षेत्रफल = πrl1 + πrl2
Sw = πr(l1 + l2) = \(\frac { 22 }{ 7 }\) x 2.4 x (4 + 3)
= \(\frac { 22 }{ 7 }\) x 2.4 x 7
= 52.8 cm²
अतः, द्विशंकु का अभीष्ट आयतन = 30.17 cm³
एवं उसका अभीष्ट पृष्ठीय क्षेत्रफल = 52.8 cm² है।
![]()
प्रश्न 3.
एक टंकी जिसका आन्तरिक मापन 150 cm x 120 cm x 110 cm है, में 129600 cm³ पानी है। इस पानी में कुछ छिद्रों वाली ईंटें तब तक डाली जाती हैं जब तक कि टंकी पूरी ऊपर तक न भर जाये। प्रत्येक ईंट अपने आयतन का \(\frac { 1 }{ 17 }\) पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm x 7.5 cm x 6.5 cm है, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं ताकि उसमें से पानी बाहर न बहे।
हल :
मान लीजिए कि टंकी में n ईंटें डाली जा सकती है। टंकी में पानी का आयतन = 129600 cm²
टंकी का आयतन V = 150 x 120 x 110
= 19,80,000 cm³.
n ईंटों का आयतन = n x 22.5 x 7.5 x 6.5.
= 1096.875 n cm³.
n ईंटों द्वारा सोखे गए पानी का आयतन = \(=\frac{1096 \cdot 875 n}{17} \mathrm{cm}^{3}\)
= 64.522 n cm³.
प्रश्नानुसार, टंकी का आयतन = ईंटों का आयतन + जल का आयतन – ईंटों द्वारा गए जल का आयतन
1980000 = 1096.875 n+ 129600 – 64.522 n
1096.875 n – 64.522 n = 1980000 – 129600
1032.353 n = 1850400
\(n=\frac{1850400}{1032 \cdot 353}=1792 \cdot 41\)
= 1792
ईंटें। अतः, ईंटों की अभीष्ट संख्या = 1792 है।
प्रश्न 4.
किसी महीने के 15 दिनों में एक नदी की घाटी में 10 cm वर्षा हुई। यदि इस घाटी का क्षेत्रफल 7280 km² है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी जबकि प्रत्येक नदी 1072 km लम्बी, 75 m चौड़ी और 3 m गहरी है।
हल :
मान लीजिए कि वर्षा के जल के तल की ऊँचाई x = 10 cm = \(\frac{10}{1,00,000}\) km एवं घाटी का क्षेत्रफल A = 7280 km². नदी की लम्बाई l = 1072 km, चौड़ाई b = 75 m = 0.075 km
एवं ऊँचाई (गहराई) h = 3 m = 0.003 km
तथा नदियों की संख्या n = 3.
वर्षा के जल का आयतन V1 = \(A \times x=\frac{7280 \times 10}{1,00,000}\)
V1 = 0.72800 km³
तीनों नदियों का आयतन = n × l × b × h
V2 = 3 × 1072 × 0.075 × 0.003
V2 = 0.7236 km³.
अतः, वर्षा के जल का आयतन लगभग तीनों नदियों के जल के आयतन के योग के बराबर है।
![]()
प्रश्न 5.
टीन की बनी एक तेल की कुप्पी 10 cm लम्बे बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8 cm और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनने में लगी टीन की चादर का क्षेत्रफल ज्ञात कीजिए (देखिए संलग्न आकृति)।
हल :
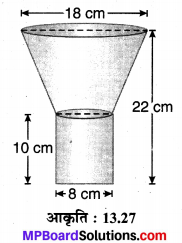
मानलीजिए एकटीन की बनी तेल की कुप्पी h1 = 10cm लम्बे एक बेलन जिसका व्यास d1 = 2r1 = 8 cm ⇒ r1 = \(\frac { 8 }{ 2 }\) cm = 4 cm है पर एक शंकु छिन्नक जिसका ऊपरी व्यास d2 = 2r2 = 18 cm
r2 = \(\frac { 18 }{ 2 }\) = 9 cm से मिलकर बनी है। कुप्पी की कुल ऊँचाई h = 22 cm है, तो शंकु-छिन्नक की ऊँचाई h2 = h – h1 = 22 – 10 = 12 cm है। सुविधा हेतु कुप्पी के शंकु-छिन्नक को संलग्न चित्र में दिखाया गया है।
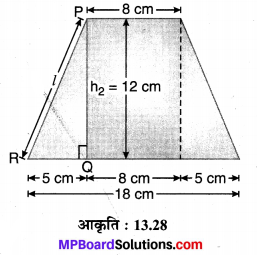
मान लीजिए शंकु-छिन्नक की तिर्यक ऊँचाई l cm है। आकृति के अनुसार, समकोण ∆PQR में ∠PQR = 90°, PQ = h2 = 12 cm एवं RQ = \(\frac{18-8}{2}=\frac{10}{2}=5 \mathrm{cm}\)
अब समकोण ∆POR में पाइथागोरस प्रमेय से,
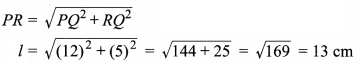
अब कुप्पी का कुल वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंकु छिन्नक का वक्र पृष्ठीय क्षेत्रफल
Sc = 2πr1h1 + πl(r1 + r2)
= 2 × π × 4 × 10 + π × 13 (4 + 9)
= 80π + 169π
= 249π
= 249 × \(\frac { 22 }{ 7 }\)
= \(\frac{5478}{7}=782 \frac{4}{7} \mathrm{cm}^{2}\)
अतः, कुप्पी को बनाने के लिए आवश्यक टीन का अभीष्ट क्षेत्रफल = \(782 \frac{4}{7} \mathrm{cm}^{2}\) है।
प्रश्न 6.
शंकु के एक छिन्नक के लिए पूर्व स्पष्ट किए गए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए जो अनुच्छेद 13.5 में दिए गए हैं, जो कि निम्न प्रकार हैं
(i) शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल Sc = π(r1 + r2)l जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
(ii) शंकु के छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल
SW = π(r1 + r2)l + πr12 + πr22 जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
हल :
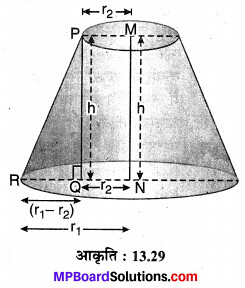
(i) मान लीजिए शंकु-छिन्नक के दोनों वृत्ताकार सिरों की त्रिज्याएँ क्रमश: NR = r1 एवं MP = r2 मात्रक तथा उनके बीच की दूरी (शंकु-छिन्नक की ऊँचाई)
= h मात्रक है = MN
P से RN पर PQ ⊥ RN डालिए। अब MNQP
एक आयत है। जिसमें PQ = MN = h मात्रक एवं QN = PM = r2 मात्रक है।
RQ = RN – QN
= (r1 – r2) मात्रक
मान लीजिए PR = छिन्नक की तिर्यक ऊँचाई
= l मात्रक
समकोण ∆PQR में पाइथागोरस प्रमेय से,
PR² = PQ² + RQ²
l² = h² + (r1 – ri)
\(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
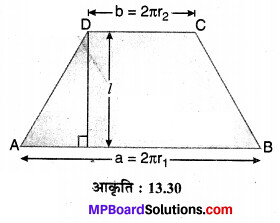
यदि हम छिन्नक के वक्र पृष्ठ को एक खड़ी रेखाखण्ड के द्वारा काटकर खोल दें तो हमको एक समलम्ब चतुर्भुज प्राप्त होगा जिसमें दोनों समान्तर रेखाओं के मान क्रमश: AB = a = 2πr1 तथा CD = b = 2πr2 होंगे तथा बीच की दूरी = l मात्रक (देखिए संलग्न आकृति) हम जानते हैं कि समलम्ब चतुर्भुज का क्षेत्रफल \(=\frac{l(a+b)}{2}\)
\(S_{c}=l\left(\frac{2 \pi r_{1}+2 \pi r_{2}}{2}\right)\)
Sc = πl(r1 + r2)
(ii) जहाँ \(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
एवं सम्पूर्ण पृष्ठ का क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + दोनों वृत्ताकार सिरों का क्षेत्रफल
Sw = Sc + πr12 + πr22
Sw = πl(r1 + r2) + πr12 + π22
\(l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
इति सिद्धम्
![]()
प्रश्न 7.
शंकु के एक छिन्नक के लिए पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, आयतन का वह सूत्र सिद्ध कीजिए, जो अनुच्छेद 13.5 में दिया गया है, जो निम्न प्रकार है : आयतन \(\boldsymbol{V}=\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\)
हल :
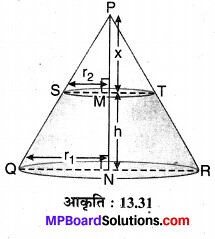
मान लीजिए शंकु छिन्नक के वृत्ताकार फलकों की त्रिज्याएँ क्रमशः r1 एवं r2 है जहाँ r1 > r2 एवं उसकी ऊँचाई (दोनों फलकों के बीच की दूरी) = h मात्रक है। उस शंक को पूरा कीजिए जिसका यह छिन्नक भाग है।
मान लीजिए शंकु की ऊर्ध्वाधर काट PQR हैं तथा ST|| QR है एवं छोटे शंकु का शीर्ष लम्ब PM =x मात्रक है, तो बड़े शंकु का शीर्ष लम्ब PN = PM + MN
= (x + h) मात्रक
समकोण ∆PNQ में SM || QN है।
∆PMS ~ ∆PNQ
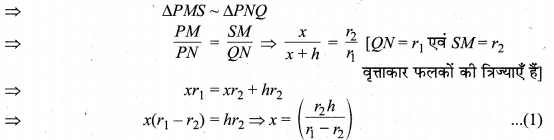
छिन्नक का आयतन = बड़े शंकु का आयतन – छोटे शंकु का आयतन
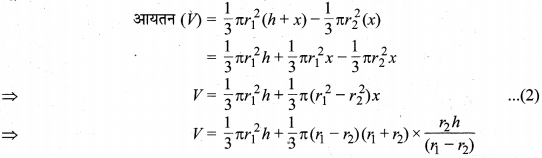
[समीकरण (1) सेx का मान (2) में रखने पर]
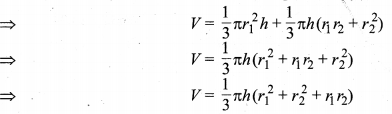
इति सिद्धम्