In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4
प्रश्न 1.
पानी पीने वाला एक गिलास 14 cm ऊँचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 cm और 2 cm हैं। इस गिलास की धारिता ज्ञात कीजिए।
हल :
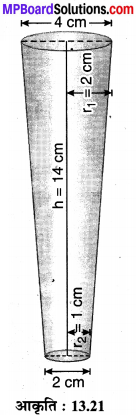
मान लीजिए दिए हुए शंकु छिन्नक की ऊँचाई h = 14 cm, वृत्ताकार सिरों के व्यास क्रमशः d1 = 2r1 = 4 cm एवं d2 = 2r2 = 2 cm
r1 = \(\frac { 4 }{ 2 }\) = 2 cm एवं r2 = \(\frac { 2 }{ 2 }\) = 1 cm है।
चूँकि शंकु के छिन्नक का आयतन = \(\frac { 1 }{ 3 }\) πh[r12 + r22 + r1r2]
⇒ गिलास की धारिता = \(\frac{1}{3} \times \frac{22}{7}\) x 14[(2)² + (1)² + (2) (1)]
= \(\frac { 44 }{ 3 }\)[4+1+2]
= \(\frac { 308 }{ 3 }\)
= \(102\frac { 2 }{ 3 }\) cm³
अतः, गिलास की अभीष्ट धारिता \(102\frac { 2 }{ 3 }\) cm³
प्रश्न 2.
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 cm है तथा इसके वृत्तीय सिरों के परिमाप (परिधियों) 18 cm एवं 6 cm हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
मान लीजिए शंकु के छिन्नक की तिर्यक ऊँचाई l = 4 cm एवं वृत्तीय सिरों के परिमाप (परिधियाँ) क्रमश: C1 = 18 cm एवं C2 = 6 cm दिये गये हैं।
चूँकि छिन्नक का वक्र पृष्ठीय क्षेत्रफल = \(l\left[\frac{C_{1}+C_{2}}{2}\right]\)
\(S_{c}=4\left[\frac{18+6}{2}\right]\)
= 4 x \(\frac { 24 }{ 2 }\)
= 4 x 12
= 48 cm²
अतः, शंकु के छिन्नक का अभीष्ट वक्र पृष्ठीय शेषफल = 48 cm² है।
![]()
प्रश्न 3.
एक तुर्की टोपी शंकु के छिन्नक के आकार की है (देखिए संलग्न आकृति)। यदि.इसके खुले सिरे की त्रिज्या 10 cm तथा ऊपरी सिरे की त्रिज्या 4 cm है और टोपी की तिर्यक ऊँचाई 15 cm है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए।
हल :
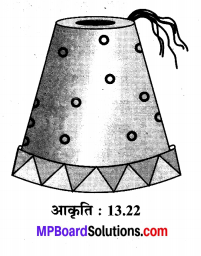
मान लीजिए शंकु के छिन्नकाकार टोपी की तिर्यक ऊँचाई l = 15 cm, सिरों की त्रिज्याएँ r1 = 10 cm एवं r2 = 4 cm दी हैं।
चूँकि शंकु के छिन्नक का वक्रपृष्ठीय क्षेत्रफल
SC = πl(r1 + r2)
SC = \(\frac { 22 }{ 7 }\) x 15(10 + 4)
= \(\frac { 22 }{ 7 }\) x 15 x 14
= 660 cm²
ऊपरी वृत्ताकार सिरे का क्षेत्रफल
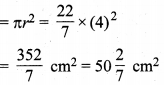
टोपी के पदार्थ का कुल क्षेत्रफल
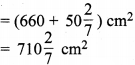
अतः, टोपी के पदार्थ का अभीष्ट क्षेत्रफल = \(710 \frac{2}{7} \mathrm{cm}^{2}\) है।
प्रश्न 4.
धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकार का है जिसकी ऊँचाई 16 cm है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमशः 8 cm और 20 cm हैं। Rs 20 प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के – लिए प्रयुक्त धातु की चादर का मल्य Rs 8 प्रति 100 cm² की दर से ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :
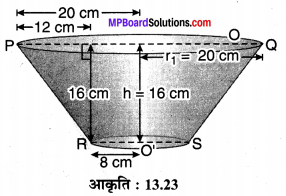
मान लीजिए कि धातु की चादर से बने एक छिन्नक के आकार के बर्तन की ऊँचाई h= 16 cm
ऊपरी एवं निचले सिरों की त्रिज्याएँ क्रमशः r1 = 20 cm एवं r2 = 8 cm हैं।
छिन्नक का आयतन = \(\frac { 1 }{ 3 }\) πh[r12 + r22 + r1r2]
V = \(\frac { 1 }{ 3 }\) x 3.14 x 16 [(20)² + (8)² + 20 x 8]
= \(\frac { 1 }{ 3 }\) x 50.24 [400 + 64 + 160]
= \(\frac { 1 }{ 3 }\) x 50.24 x 624
= \(\frac{31349.76}{3} \mathrm{cm}^{3}\)
छिन्नक का आयतन = 10449.92 cm³
दूध का आयतन = 10.45 लीटर
दूध का मूल्य = दूध का आयतन x दर
= 10.45 x 20
= Rs 209
अतः, दूध का अभीष्ट मूल्य = Rs 209 है।
सविधा के लिए छिन्नक का एक भाग संलग्न आकृति में दर्शाया गया है। मान लीजिए PR = l तथा OP = r1 = 20 cm
एवं O’R = r2 = 8 cm
तथा OO’ = h = 16 cm (दी है)
तो समकोण ∆RMP में,
MP = OP – OM
= OP – O’R
= r1 – r2
= 20 – 8
= 12 cm
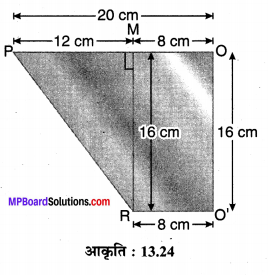
एवं MR = OO’ = h = 16 cm
समकोण ∆RMP में पाइथागोरस प्रमेय से,
![]()
छिन्नक का वक्रपृष्ठ S. = πl(r1 + r2)
SC = 3.14 x 20(20 + 8)
= 3.14 x 20 x 28
= 1758.4 cm²
वृत्तीय आधार का क्षेत्रफल = πr22 = 3.14 x (8)²
= 3.14 x 64
= 200.96 cm²
धातु-चादर का कुल क्षेत्रफल, Sw = 1758.4 + 200.96 = 1959.36
धातु-चादर का मूल्य = धातु-चादर का क्षेत्रफल x दर
= \(\frac{1959 \cdot 36 \times 8}{100}\)
= Rs 156.75
अतः, धातु-चादर का अभीष्ट मूल्य = Rs 156.75 है।
![]()
प्रश्न 5.
20 cm ऊँचाई और शीर्ष कोण (Vertical angle) 60° वाले एक शंकु को उसकी ऊँचाई के बीचों-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समान्तर है। यदि इस प्राप्त शंकु-छिन्नक को व्यास \(\frac { 1 }{ 16 }\) cm वाले एक तार के रूप में बदल दिया जाता है, तो तार की लम्बाई ज्ञात कीजिए।
हल :
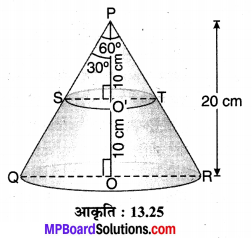
मान लीजिए ऊँचाई h = PO = 20 cm और शीर्ष कोण ∠OPR = 60° वाले शंकु को उसकी ऊँचाई के बीचों-बीच (मध्य बिन्दु) O’ से जाने वाले आधार के समान्तर तल द्वारा दो भागों में विभक्त किया गया है, जहाँ
PO’ = OO’ = h’ = \(\frac { 20 }{ 2 }\) = 10 cm [जहाँ h’ छिन्नक की ऊँचाई]
∆PQR एक समद्विबाहु ∆ है तथा PO उसका शीर्ष लम्ब
⇒ ∠QPO = ∠SPO’ = \(\frac { 60 }{ 2 }\) = 30°
माना OQ = r1 तथा O’S = r2

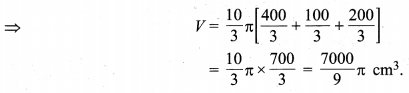
मान लीजिए तार की लम्बाई l cm है तथा व्यास d = 2r = \(\frac { 1 }{ 16 }\) cm
r = \(\frac { 1 }{ 32 }\) cm
तार का आयतन = छिन्नक का आयतन
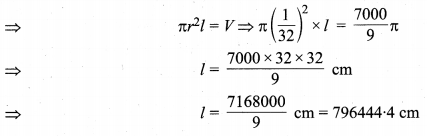
अतः, तार की अभीष्ट लम्बाई = 796444.4 cm या 7964.4 m है।