MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions

MP Board Class 10th Maths Chapter 13 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 13 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी वर्षा जल संग्रहण तन्त्र में, 22 m x 20 m की छत से वर्षा-जल बहकर 2 m आधार के व्यास तथा 3.5 m ऊँचाई के एक बेलनाकार टैंक में आता है। यदि टैंक भर गया हो, तो ज्ञात कीजिए कि सेमी में कितनी वर्षा हुई? जल संरक्षण पर अपने विचार व्यक्त कीजिए।
हल :
मान लीजिए वर्षा x cm हुई। छत की विमाएँ 22 m x 20 m दी हैं तथा दिए हुए बेलनाकार टैंक का व्यास d = 2r = 2 m ⇒ r = \(\frac { 2 }{ 2 }\) = 1 m तथा ऊँचाई h = 3.5 m दी है।
∵ वर्षा जल का आयतन = बेलनाकार टैंक का आयतन
⇒ छत की विमाएँ x वर्षा जल की ऊँचाई = πr²h.
= 22 m x 20 m x \(\frac { x }{ 100 }\) m
= \(\frac { 22 }{ 7 }\) x (1)² x 3.5
= \(x=\frac{22}{7} \times \frac{1 \times 3 \cdot 5 \times 100}{22 \times 20}\)
= 2.5
अतः अभीष्ट वर्षा कुल 2.5 cm हुई।
जल संरक्षण : विज्ञान में हमारे संसाधनों का प्रबन्धन’ अध्याय देखिए।

प्रश्न 2.
एकठोस लोहे के घनाभ की विमाएँ 4.4 m x 2.6 m x 1.0 m हैं। इसे पिघलाकार 30 cm आन्तरिक त्रिज्या और 5 cm मोटाई का एक खोखला बेलनाकार पाइप बनाया गया है। पाइप की लम्बाई ज्ञात कीजिए।
हल :

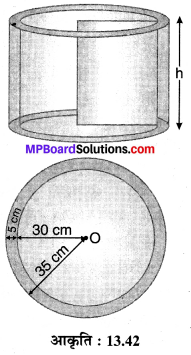
मान लीजिए खोखले बेलनाकार पाइप की लम्बाई = h cm है।
पाइप की मोटाई x = 5 cm तथा आन्तरिक त्रिज्या r_i = 30 cm
⇒ पाइप की बाह्य त्रिज्या r₀ = r_i + x = 30 + 5 = 35 cm
तथा ठोस लोहे के घनाभ की विमाएँ दी हैं।
4.4 m x 2.6 m x 1.0 m
⇒ 440 cm x 260 cm x 100 cm
ठोस घनाभ का आयतन V = 440 x 260 x 100 cm³ ….(1)
बेलनाकार पाइप का आयतन


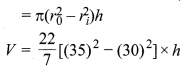
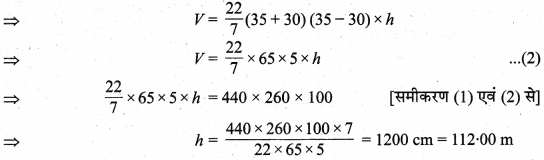
अतः, बेलनाकार पाइप की अभीष्ट लम्बाई = 112.00 m है।

प्रश्न 3.
5.4m चौड़ी और 18 m गहरी एक नहर में पानी 25 km/h की गति से बह रहा है। इसमें 40 मिनट में कितने क्षेत्रफल की सिंचाई हो सकती है, यदि सिंचाई के लिए 10 cm गहरे पानी की आवश्यकता है?
हल :
दिया है : नहर की चौड़ाई b = 5.4 m, गहराई h = 1.8 m एवं जल की गति 25 km/h तथा धारा प्रवाह का समय 40 मिनट = \(\frac { 40 }{ 60 }\) घण्टे = \(\frac { 2 }{ 3 }\) घण्टे।
\(\frac { 2 }{ 3 }\) घण्टे में जल प्रवाह की लम्बाई l = 25 km/h x \(\frac { 2 }{ 3 }\) h
\(=\frac{50}{3} \mathrm{km}=\frac{50,000}{3} \mathrm{m}\)
∴ नहर में प्रवाहित कुल जल का आयतन

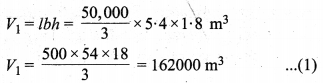
मान लीजिए सिंचाई हेतु क्षेत्र का क्षेत्रफल = A m²
तो क्षेत्र को सिंचाई के लिए आवश्यक जल का आयतन
⇒ V₂ = A × x (जहाँ x = 10 cm = 0.10 m दिया है)
⇒ V₂ = A × 0.10 = 0.10 A m² …(2)
∵ क्षेत्र की सिंचाई के लिए आवश्यक जल का आयतन = नहर द्वारा उस समय में उपलब्ध जल का आयतन
⇒ 0.10 A = 162000 [समी. (1) एवं (2) से]
⇒ \(A=\frac{162000}{0 \cdot 10}=1620000 \mathrm{m}^{2}\)
= 162
हेक्टेयर अतः, सिंचाई किए जा सकने वाले अभीष्ट क्षेत्र का क्षेत्रफल = 1620000 m² अथवा 162 हेक्टेअर है।

प्रश्न 4.
एक ठोस धातु के बेलन के दोनों किनारों से उसी व्यास के अर्द्धगोले के रूप में धातु निकाली गयी। बेलन की ऊँचाई 10 cm तथा आधार की त्रिज्या 4.2 cm है। शेष बचे बेलन को पिघलाकर 1.4 cm मोटी बेलनाकार तार बनायी गयी। तार की लम्बाई ज्ञात कीजिए। (π = \(\frac { 22 }{ 7 }\) लीजिए।)
हल :

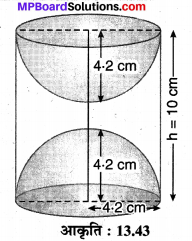
दिया है: एक बेलनाकार धातु का ठोस जिसकी ऊँचाई h = 10 cm तथा आधार की त्रिज्या r = 4.2 cm है तथा इसके दोनों सिरों से एक अर्द्धगोला त्रिज्या 4.2 cm का काटकर निकाल दिया गया है। शेष भाग को पिघलाकर एक 1.4 cm मोटी अर्थात् व्यास d = 2r’ = 1.4 cm
⇒ r’ = \(\frac { 1.4 }{ 2 }\) = 0.7 cm त्रिज्या का तार बनाया गया है। मान लीजिए तार की लम्बाई l cm है, तो
तार का आयतन = πr’²l = \(\frac { 22 }{ 7 }\) x (0.7)² l
⇒ V = 1.54 l cm³ ..(1)
बेलन का आयतन V₁ = πr²h = \(\frac { 22 }{ 7 }\) x (4.2)² x 10
⇒ V₁ = 22 x 2.52 x 10
= 554.4 cm³.
दो अर्द्धगोलों का आयतन V₂ = 2 x \(\frac { 2 }{ 3 }\) πr³
⇒ \(V_{2}=\frac{4}{3} \times \frac{22}{7} \times(4 \cdot 2)^{3}=\frac{6519 \cdot 744}{21}\)
⇒ V₂ = 310.464 cm³
शेष बेलन का आयतन V = V₁ – V₂
⇒ V = 554.4 – 310.464
= 243.936 cm³ …(2)
⇒ 1.54 l = 243.936 [समीकरण (1) एवं (2) से]
⇒ l = \(\frac { 243.963 }{ 1.54 }\)
= 158.4 cm
= 1.584 m
अतः, तार की अभीष्ट लम्बाई = 158.4 cm अर्थात् 1.584 m है।

प्रश्न 5.
एक अर्द्धगोलीय बर्तन का आन्तरिक व्यास 36 cm है। वह तरल पदार्थ से भरा है। इस तरल को 72 बेलनाकार बोतलों में डाला गया है। यदि एक बेलनाकार बोतल का व्यास 6 cm हो, तो प्रत्येक बोतल की ऊँचाई ज्ञात कीजिए, जबकि इस क्रिया में 10% तरल गिर जाता है।
हल :
दिया है : एक अर्द्ध गोलीय बर्तन का व्यास d = 2r = 36 cm
r = \(\frac { 36 }{ 2 }\) = 18 cm.
इस बर्तन में भरे तरल के आयतन का 10% भाग बोतल भरने में गिर जाता है। एक बोतल का व्यास d = 2r’ = 6 cm
r’ = \(\frac { 6 }{ 2 }\) = 3 cm तथा बोतलों की संख्या n = 72 है।
मान लीजिए कि प्रत्येक बोतलों में तरल h ऊँचाई तक भरा जाता है।
∴अर्द्ध गोलाकार बर्तन में भरे तरल का आयतन V₁ = \(\frac { 2 }{ 3 }\) πr³
⇒ V₁ = \(\frac { 2 }{ 3 }\) π (18)³
= 3888 π
गिरने वाले तरल का आयतन = 10% V₁
⇒ V₂ = \(\frac { 10 }{ 100 }\) x 3888 π
= 388.8 π
शेष तरल का आयतन V = V₁ – V₂
= 3888 π – 388.8 π
⇒ V = 3499.2 π …..(1)
n बोतलों के तरल का आयतन = n x πr’² h
⇒ V = 72 x π x (3)²h
= 648 πh …(2)
⇒ 648 πh = 3499.2 π [समीकरण (1) एवं (2) से]
⇒ h = \(\frac { 3499.2 }{ 648 }\)
= 5.4 cm
अतः, बोतलों में तरल की अभीष्ट ऊँचाई = 5.4 cm है।

प्रश्न 6.
10 cm भुजा वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्ध गोला रखा हुआ है। अद्ध गोल का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस के सम्पूर्ण पृष्ठीय क्षेत्र को पेंट करवाने का Rs 5 प्रति 100 वर्ग सेमी की दर से व्यय ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :

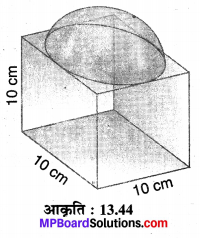
दिया है: a = 10 cm भुजा वाला एक घनाकार ब्लॉक जिसके ऊपरी तल पर एक अधिकतम व्यास का अर्द्ध गोला रखा है।
⇒ अर्द्ध गोले का अधिकतम व्यास d = घन की भुजा a = 10 cm
⇒ अर्द्ध गोले की त्रिज्या = \(\frac { 10 }{ 2 }\) = 5 cm
घन के ऊपरी तल पर r = 5 cm त्रिज्या का एक वृत्ताकार भाग अर्द्ध गोले से ढका है।
चूँकि घन का सम्पूर्ण पृष्ठीय क्षेत्रफल S_w = 6a²
S_w = 6(10)²
= 600 cm²
वृत्ताकार भाग का क्षेत्रफल A = πr² = π(5)² = 25π cm²
अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल S_C = 2πr²
= 2π(5)²
S_C = 50 π cm²

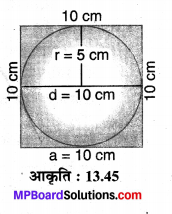
दिए संयुक्त ठोस का सम्पूर्ण पृष्ठ
S = घन का सम्पूर्ण पृष्ठ + अर्द्ध गोले का वक्र पृष्ठीय क्षेत्रफल – वृत्त का क्षेत्रफल
= S_w + S_C – A
= 600 + 50π – 25π
= 600 + 25π
= 600 + 25 x 3.14
= (600 + 78.50) cm²
S = 678.5 cm²
रंग करवाने का व्यय = क्षेत्रफल x दर
व्यय = 678.5 x \(\frac { 5 }{ 100 }\)
= Rs 33.93
अतः, अर्द्धवृत्त का अधिकतम व्यास = 10 cm
एवं ठोस पर रंग करवाने का कुल व्यय = Rs 33.93 है।

प्रश्न 7.
धातु के 3.5 cm व्यास तथा 3 cm ऊँचे 504 शंकुओं को पिघलाकर एक धात्विक गोला बनाया गया है। गोले का व्यास ज्ञात कीजिए। अतः इसका पृष्ठीय क्षेत्रफल भी ज्ञात कीजिए।
हल :
दिया है : 504 ठोस शंकु जिनमें प्रत्येक का व्यास d = 2r = 3.5 = \(\frac { 7 }{ 2 }\) = cm
r = \(\frac { 7 }{ 2 }\) cm तथा ऊँचाई h = 3 cm. इनको पिघलाकर एक ठोस गोला बनाया गया है। मान लीजिए गोले की त्रिज्या = R cm है, तो
गोले का आयतन V = \(\frac { 4 }{ 3 }\)πR³ ….(1)
एवं , 504 शंकुओं का आयतन

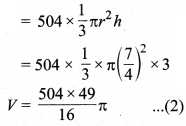
गोले का आयतन = 504 शंकुओं का आयतन

अतः, गोले का अभीष्ट व्यास = 21 cm एवं उसका पृष्ठीय क्षेत्रफल = 1386 cm² है।

प्रश्न 8.
अचानक बाढ़ आने पर कुछ कल्याणकारी संस्थाओं ने मिलकर सरकार को उसी समय 100 टैंट लगवाने के लिए कहा तथा इस पर आने वाले खर्च का 50% देने की पेशकश की। यदि प्रत्येक टेंट का निचला भाग बेलनाकार है जिसका व्यास 4.2 m है तथा ऊँचाई 4 m है तथा ऊपरी भाग उसी व्यास का शंकु है जिसकी ऊँचाई 2.8m है, और इस पर लगने वाले कैनवास की लागत Rs 100 प्रति वर्ग मीटर है, तो ज्ञात कीजिए कि इन संस्थाओं को कितनी राशि देनी होगी? इन संस्थाओं द्वारा किन मूल्यों का प्रदर्शन किया गया?
हल :

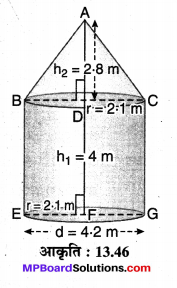
ज्ञात है टैंट का निचला भाग, व्यास d = 2r = 4.2 m
r = \(\frac { 4.2 }{ 2 }\) = 2.1
अर्थात् त्रिज्या r = 2.1 m का एक बेलन जिसकी ऊँचाई h₁ = 4 m
एवं ऊपरी भाग r = 2.1 m की त्रिज्या तथा ऊँचाई h₂ = 28 m का
एक शंकु l मान लीजिए शंकु की तिर्यक ऊँचाई = l m है।

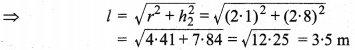
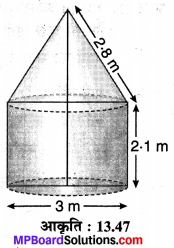
बेलनाकार भाग का वक्रपृष्ठीय क्षेत्रफल
S_C1 = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 2.1 x 4
= 52.8 m²
एवं शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_C2 = πrl
= \(\frac { 22 }{ 7 }\) x 2.1 x 3.5
= 23.1 cm²
टेंट के कैनवास का कुल क्षेत्रफल = S_C = S_C1 + S_C2
S_C = 52.8 + 23.1 = 75.9 m²
100 टैंटों के लिए आवश्यक कैनवास का कुल क्षेत्रफल
= 100 x 75.9
= 7590 m²
कुल व्यय = कैनवास का क्षेत्रफल – दर
= 7590 x 100
= Rs 759000
संस्थाओं की हिस्सेदारी = 50% x Rs 759000
= Rs \(\frac { 50 }{ 100 }\) x 759000
= Rs 379500
अतः, संस्थाओं को Rs 379500 की धनराशि देनी होगी तथा ये संस्थाएँ मानवीय मूल्यों का प्रदर्शन कर रही हैं।

प्रश्न 9.
संलग्न आकृति में एक टैंट बेलन के ऊपर लगे उसी व्यास वाले शंकु के आकार का है। बेलनाकार भाग की ऊँचाई तथा व्यास क्रमश: 2.1 m तथा 3 m हैं तथा शंक्वाकार भाग की तिरछी ऊँचाई 2.8 m है। टैंट को बनाने में लगे कैनवास का मूल्य ज्ञात कीजिए, यदि कैनवास का भाव Rs 500 प्रति वर्ग मीटर है।
हल :

मान लीजिए टैंट का निचला भाग बेलनाकार है जिसकी ऊँचाई h = 2.1 m तथा व्यास d = 2r = 3 m है। अर्थात् त्रिज्या r = \(\frac { 3 }{ 2 }\) m है एवं ऊपरी शंक्वाकार भाग का व्यास बेलनाकार भाग के व्यास के बराबर अर्थात् त्रिज्या r = \(\frac { 3 }{ 2 }\) m है तथा त्रिर्यक ऊँचाई l = 2.8 m है।
बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल
\(S_{C_{1}}=2 \pi r h=2 \times \frac{22}{7} \times \frac{3}{2} \times 2 \cdot 1=19 \cdot 8 \mathrm{m}^{2}\)
एवं शंक्वाकार भाग का वक्रपृष्ठीय क्षेत्रफल
\(S_{C_{2}}=\pi r l=\frac{22}{7} \times \frac{3}{2} \times 2 \cdot 8=13 \cdot 2 \mathrm{m}^{2}\)
टैंट का कुल वक्र पृष्ठीय क्षेत्रफल S_C = S_C1 + S_C2
⇒ S_C = 19.8 + 13.2
= 33 m²
कैनवास का क्षेत्रफल = टैंट का कुल वक्र पृष्ठीय क्षेत्रफल
= 33 m²
कैनवास का कुल मूल्य = कैनवास का क्षेत्रफल x दर (भाव)
= 33 x 500
= Rs 16,500
अतः, कैनवास का अभीष्ट मूल्य = Rs 16,500 है।

प्रश्न 10.
एक शंक्वाकार बर्तन, जिसके आधार की त्रिज्या 5 cm तथा ऊँचाई 24 cm है, पानी से पूरा भरा है। उस पानी को एक बेलनाकार बर्तन, जिसकी त्रिज्या 10 cm है, में डाल दिया जाता है। बेलनाकार बर्तन में कितनी ऊँचाई तक पानी भर जायेगा?
हल :
मान लीजिए कि शंक्वाकार बर्तन के आधार की त्रिज्या r1 = 5 cm तथा ऊँचाई h1 = 24 cm है यह पूरा पानी से भरा है तथा इसका पानी एक बेलनाकार बर्तन जिसकी त्रिज्या r2 = 10 cm है में डाल . दिया जाता है। पुनः मान लीजिए कि बेलनाकार बर्तन में पानी के स्तर की अभीष्ट ऊँचाई h2 cm है, तो प्रश्नानुसार,
बेलनाकार बर्तन में पानी का आयतन = शंक्वाकार बर्तन की धारिता

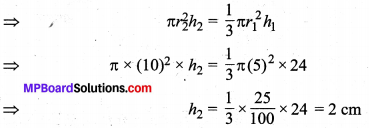
अतः, बेलनाकार बर्तन में पानी के स्तर की अभीष्ट ऊँचाई = 2 cm है।

प्रश्न 11.
12 cm व्यास वाला एक गोला, एक लम्ब वृत्तीय बेलनाकार बर्तन में डाल दिया जाता है, जिसमें कुछ पानी भरा है। यदि गोला पूर्णतया पानी में डूब जाता है, तो बेलनाकार बर्तन में पानी का स्तर \(3\frac { 5 }{ 9 }\) सेमी ऊँचा उठ जाता है। बेलनाकार बर्तन का व्यास ज्ञात कीजिए।
हल :
मान लीजिए D = 12 cm व्यास अर्थात् R = \(\frac { 12 }{ 2 }\) = 6 cm त्रिज्या वाला एक गोला एक बेलनाकार बर्तन जिसका व्यास d cm है में डाला जाता है, जिसमें कुछ पानी भरा है। पानी का स्तर h = \(3\frac { 5 }{ 9 }\) cm = \(\frac { 32 }{ 9 }\) cm बढ़ जाता है। बेलनाकार बर्तन की त्रिज्या r = \(\frac { d }{ 2 }\), है।
चूँकि बेलनाकार बर्तन में बढ़े हुए जल स्तर का आयतन = गोले का आयतन

अतः, बेलनाकार बर्तन का अभीष्ट व्यास = 18 cm है।

प्रश्न 12.
किसी राज्य में भारी बाढ़ के कारण हजारों लोग बेघर हो गए। 50 विद्यालयों ने मिलकर राज्य सरकार को 1500 टैंट लगाने के लिए स्थान तथा कैनवास देने का प्रस्ताव किया जिसमें प्रत्येक विद्यालय बराबर का अंशदान देगा। प्रत्येक टैंट का निचला भाग बेलनाकार है जिसके आधार की त्रिज्या 2.8 m तथा ऊँचाई 3.5m है। प्रत्येक टैंट का ऊपरी भाग शंकु के आकार का है। जिसके आधार की त्रिज्या 2.8m तथा ऊँचाई 2.1m है। यदि टैंट बनाने वाले कैनवास का मूल्य Rs 120 प्रति वर्ग मीटर है, तो प्रत्येक विद्यालय द्वारा कुल व्यय में अंशदान ज्ञात कीजिए। इस प्रश्न का कौन-सा मूल्य जनित होता है?
हल :

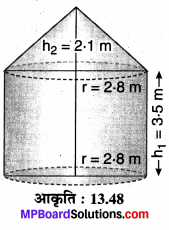
मान लीजिए टैंट का निचला भाग त्रिज्या r1 = 2.8 m एवं ऊँचाई h1 = 3.5 m का बेलन है तथा ऊपरी भाग त्रिज्या r2 = 2:8 m एवं ऊँचाई h2 = 2.1 m का शंकु है और मान लीजिए शंकु की त्रिर्यक ऊँचाई l m है, तो

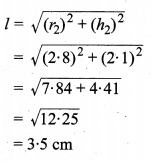
बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_c1 = 2πr₁h₁
= 2π x 2.8 x 3.5
S_c1 = 19.6 π m²
एवं शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_c2 = πrl
= π x 2.8 x 3.5 .
S_c1 = 9.8 π m²
टैंट का कुल वक्र पृष्ठीय क्षेत्रफल
S_c = S_c1 + S_c2
= 19.6 π + 9.8 π
= 29.47 π
= 29.4 x \(\frac { 22 }{ 7 }\) m²
S_c = 92.4 m² = कैनवास का क्षेत्रफल
1500 टैंटों के लिए आवश्यक कैनवास का कुल क्षेत्रफल
= 1500 x 92.4 m²
= 138600.0 m²
कुल व्यय = कैनवास का क्षेत्रफल – दर
= 138600 x 120
= Rs 16632000
प्रत्येक विद्यालय का व्यय में अंशदान

= Rs 3,32,640
अतः, प्रत्येक विद्यालय द्वारा कुल व्यय में अभीष्ट अंशदान = Rs 3,32,640 है।

प्रश्न 13.
तीन ठोस गोले जिनके व्यास क्रमशः 2 cm. 12 cm और 16 cm हैं. पिघलाकर एक ठोस गोला बनाया गया। इस प्रकार बने ठोस गोले का अर्द्धव्यास ज्ञात कीजिए।
हल :
यहाँ,
2R₁ = 2 cm
⇒ R₁ = \(\frac { 2 }{ 2 }\) = 1 cm
2R₂ = 12 cm
⇒ R₂ = \(\frac { 12 }{ 2 }\) = 6cm
2R₃ = 16 cm
⇒ R₃ = \(\frac { 16 }{ 2 }\) = 8 cm
माना गोले का अर्द्धव्यास = R cm हो, तो
प्रश्नानुसार,

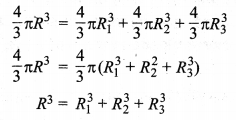
= (1)³ + (6)³ + (8)³
= 1 + 216 + 512
R³ = 729 = (9)³
R = 9 cm
अतः, गोले की अभीष्ट त्रिज्या (अर्द्धव्यास) = 9 cm है।

प्रश्न 14.
एक 8 cm व्यास वाले धातु के बेलन को पिघलाकर 12 cm व्यास वाले कितने गोले बनाए जा सकते हैं? बेलन की ऊँचाई 90 cm है।
हल :
ज्ञात है : बेलन का व्यास d = 8 cm
r = 8/2 = 4 cm, ऊँचाई h= 90 cm, गोले का व्यास D = 12 cm
⇒ गोले की त्रिज्या R = \(\frac { 12 }{ 2 }\) = 6 cm
मान लीजिए बनाए गए गोले की संख्या = n प्रश्नानुसार,
∵ n गोलों का आयतन = बेलन का आयतन
⇒ n x \(\frac { 4 }{ 3 }\) πR³ = π(r)² x h
⇒ \(\frac { 4 }{ 3 }\)nR³ = r²h
⇒ \(\frac { 4 }{ 3 }\)n x (6)³ = (4)² x 90
⇒ \(\frac { 4 }{ 3 }\) x 216 n = 16 x 90
⇒ \(n=\frac{16 \times 90 \times 3}{4 \times 216}=5\) गोले
अतः, अभीष्ट गोलों की संख्या = 5 है।

प्रश्न 15.
6 cm व्यास के एक लोहे के गोले को पिघलाकार उससे एक बेलनाकार तार खींचा गया है। यदि तार का व्यास 0.2 cm हो, तो तार की लम्बाई ज्ञात कीजिए।
हल :
दिया है : गोले का व्यास D = 2R = 6 cm ⇒ R = \(\frac { 6 }{ 2 }\) cm = 3 cm
बेलनाकार तार का व्यास d = 2r = 0.2 cm
⇒ r = \(\frac { 0.2 }{ 2 }\) cm = 0.1 cm मान लीजिए कि बेलनाकार तार की लम्बाई = l cm
तो प्रश्नानुसार,
तार का आयतन = गोले का आयतन
⇒ πr²l = \(\frac { 4 }{ 3 }\)πR³
⇒ (0.1)²l = \(\frac { 4 }{ 3 }\)(3)³
⇒ 0.01 l = 4 x 9 = 36
⇒ l = \(\frac { 36 }{ 0.01 }\)
= 3600 cm
= 36.00 m
अतः, तार की अभीष्ट लम्बाई = 36 m है।

प्रश्न 16.
एक रॉकेट लम्ब वृत्तीय बेलन के आकार का है जिसका निचला सिरा बन्द है तथा ऊपरी सिरे पर एक शंकु है जिसकी त्रिज्या बेलन की त्रिज्या के बराबर है। बेलन का व्यास एवं उसकी ऊँचाई क्रमशः 6 cm एवं 12 cm है। यदि शंक्वाकार भाग की तिर्यक ऊँचाई 5 cm हो, तो रॉकेट का कुल पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
हल :

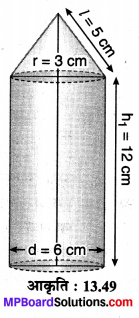
दिया है: एक बेलनाकार रॉकेट जिसका व्यास d = 2r = 6
⇒ r = \(\frac { 6 }{ 2 }\) cm
= 3 cm एवं ऊँचाई h1 = 12 cm जिसका निचला सिरा बन्द है तथा ऊपरी सिरे पर शंकु त्रिज्या r = 3 cm तथा तिर्यक ऊँचाई l = 5 cm है, जुड़ा है। मान लीजिए शंकु की ऊँचाई = h2 cm है, तो

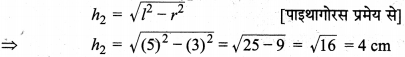
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl = π x 3 x 5 = 15π cm²
बेलनाकार वक्र पृष्ठीय क्षेत्रफल = 2πrh₁
= 2 x π x 3 x 12
= 72π cm²
आधार का क्षेत्रफल = πr² = π x (3)² = 9π cm²
कुल पृष्ठीय क्षेत्रफल = 15π + 72π + 9π = 96 π cm²
= 96 x 3.14
= 301.44 cm²
शंक्वाकार भाग का आयतन = \(\frac{1}{3} \pi r^{2} h_{2}=\frac{1}{3}(3)^{2} \times 4 \times \pi\)
= 12π cm³
बेलनाकार भाग का आयतन = πr²h₁ = π x (3)² x 12
= 108π cm³
रॉकेट का कुल आयतन = 12π + 108π
= 120π cm³
= 120 x 3.14
= 376.8 cm³
अतः रॉकेट का अभीष्ट सम्पूर्ण पृष्ठीय क्षेत्रफल = 301.44 cm²
एवं अभीष्ट आयतन = 376.8 cm³ है।

प्रश्न 17.
8 cm त्रिज्या वाला एक ठोस अर्द्ध गोला पिघलाकर उसे एक लम्ब वृत्तीय शंक में ढाला गया है। यदि शंकु के आधार की त्रिज्या 6 cm हो, तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
ठोस अर्द्ध गोले की त्रिज्या R = 8 cm, दी है, इसको पिघलाकर एक आधार त्रिज्या r = 6 cm वाले
शंकु में ढाला गया है। मान लीजिए कि शंकु की ऊँचाई h cm है,
तो प्रश्नानुसार, शंकु का आयतन = अर्द्ध गोले का आयतन

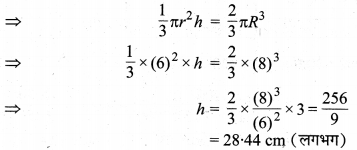
अतः, शंकु की अभीष्ट ऊँचाई = 28.44 cm (लगभग) है।

प्रश्न 18.
एक आयताकार पानी की टंकी का आधार 11 m x 6m है तथा इसमें 5m की ऊँचाई तक पानी भरा हुआ है। यदि इस टंकी के पानी को 3.5m त्रिज्या की बेलनाकार टंकी में उडेल दिया जाए, तो इस टंकी में जल स्तर की ऊँचाई ज्ञात कीजिए।
हल :
आयताकार टंकी का आधार 11 m x 6 m तथा जल की ऊँचाई 5 m दी है तथा इस जल को r = 3.5 m त्रिज्या की बेलनाकार टंकी में उडेल दिया गया है।
मान लीजिए कि बेलनाकार टंकी में जल स्तर भी ऊँचाई h m हो, तो
प्रश्नानुसार, आयताकार टंकी के जल का आयतन = बेलनाकार टंकी के जल का आयतन
⇒ 11 m x 6 m x 5 m = πr²h = \(\frac { 22 }{ 7 }\) (3.5 m)² x h m
⇒ \(h=\frac{11 \times 6 \times 5 \times 7}{22 \times 3 \cdot 5 \times 3 \cdot 5}=\frac{60}{7}=8 \cdot 6 \mathrm{m}\)
अतः,बेलनाकार टंकी में जल स्तर की अभीष्ट ऊँचाई = 8.6 cm है।

प्रश्न 19.
1.5 cm मोटी लोहे की चद्दर के बने एक आयताकार ऊपर से खुले बॉक्स को बनाने में कितना cm लोहा लगेगा यदि उसकी बाहरी विमाएँ 36 cm x 25 cm x 16.5 cm है। यदि 1 cm³ लोहे का भार 7.5g हो, तो बक्से का भार ज्ञात कीजिए।
हल :
दिया है : बक्से की बाहरी विमाएँ 36 cm x 25 cm x 16.5 cm दी हैं तथा इसकी मोटाई 1.5 cm है, अत: बक्से की आन्तरिक विमाएँ
⇒ (36 – 3)cm x (25 – 3) cm x (16.5 – 1.5) cm अर्थात् 33 cm x 22 cm x 15 cm होंगी। लोहे का घनत्व d = 7:5 g/cm³
बक्से का बाह्य आयतन = 36 x 25 x 16.5 = 14850 cm³
बक्से का आन्तरिक आयतन = 33 x 22 x 15 = 10890 cm³
बक्से में लगे लोहे का आयतन = (14850 – 10890) cm³
आयतन V = 3960 cm³
एवं बक्से का भार = आयतन V x घनत्व d
= 3960 x 7.5 g
= 29700 g
= 29.7 kg
अतः लोहे का अभीष्ट आयतन = 3960 cm³ एवं
लोहे का अभीष्ट भार = 29700 g अर्थात् 29.7 kg होगा।

प्रश्न 20.
5 mm व्यास वाले एक बेलनाकार पाइप से जल का प्रवाह 10 m/minute है। आधार व्यास 40 cm एवं गहराई 24 cm वाले शंक्वाकार बर्तन को भरने में कितना समय लगेगा?
हल :
दिया है : बेलनाकार पाइप का व्यास d₁ = 2r₁ = 5 mm = 0.5 cm ⇒ r₁ = \(\frac { 0.5 }{ 2 }\) = 0.25 cm.
पाइप में जल प्रवाह v = 10 m/minute = \(\frac { 1000 }{ 60 }\) cm/s है। इससे शंक्वाकार बर्तन को भरना है जिसकी आधार व्यास d₂ = 2r₂ = 40 cm ⇒ r₂ = \(\frac { 40 }{ 2 }\) = 20 cm, गहराई h₂ = 24 cm दी है। मान लीजिए जल पाइप इस बर्तन को भरने में t minute का समय लेता है।
t minute में पाइप द्वारा निकली जल धारा की लम्बाई h₁ = 1000 t cm
प्रश्नानुसार, पाइप द्वारा t minute में दिया गया पानी = शंक्वाकार बर्तन का आयतन

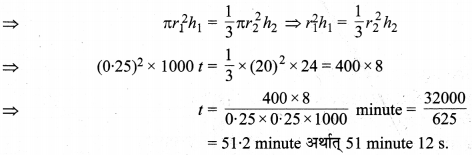
अतः, अभीष्ट समय = 51.2 minute अर्थात 51 minute एवं 12 s है।

प्रश्न 21.
14 cm व्यास वाले एक बेलनाकार पाइप से होकर 15 km/h की दर से जल एक घनाभाकार गड्ढे में जिसकी लम्बाई 50 m एवं चौड़ाई 44 m है, गिरता है। कितने समय में गड्ढे में जलस्तर 21 cm चढ़ जायेगा?
हल :
मान लीजिए बेलनाकार पाइप का व्यास d = 2r = 14 cm = 0.14 m ⇒ r = \(\frac { 0.14 }{ 2 }\) = 0.07 m
दिया है जिसमें होकर जल की धारा 15 km/h की दर से अर्थात् 15,000 m/h की दर से प्रवाहित हो रही है, जो एक गड्ढे में गिरती है। गड्ढे की लम्बाई l = 50 m. चौड़ाई b = 44 cm एवं जलस्तर की ऊँचाई h = 21 cm = 0.21 m है। मान लीजिए इसको भरने में t घण्टे लगते हैं, तो प्रश्नानुसार, पाइप से निकला जल का आयतन = गड्ढे में जल का आयतन
lbh = πr² x दर x समय
50 x 44 x 0.21 = \(\frac { 22 }{ 7 }\) x (0.07)² x 15000 x 1
\(t=\frac{50 \times 44 \times 0.21 \times 7}{22 \times 0.07 \times 0.07 \times 15000}=\frac{50 \times 44 \times 21 \times 7}{22 \times 7 \times 7 \times 150}\)
= 2 घण्टे
अतः, अभीष्ट समय = 2 घण्टे है।

प्रश्न 22.
16 cm ऊँचाई वाला एक दूध का बर्तन किसी शंकु के छिन्नक के आकार का धातु की चद्दर से बना है जिसकी नीचे एवं ऊपर के सिरों की त्रिज्याएँ क्रमशः 8 cm एवं 20 cm हैं। इसमें भरे दूध का मूल्य ज्ञात कीजिए जबकि दूध की दर Rs 22 प्रति लीटर है।
हल :

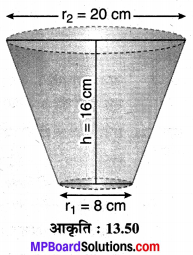
बर्तन (छिन्नक) के दोनों सिरों की त्रिज्याएँ क्रमशः r1 = 8 cm एवं r2 = 20 cm तथा ऊँचाई h = 16 cm है। दूध की दर Rs 22 प्रति लीटर, दिया है।
दूध का आयतन = छिन्नक का आयतन

अतः, दूध का अभीष्ट मूल्य = Rs 230 (लगभग) है।

प्रश्न 23.
32 cm ऊँची तथा 18 cm आधार त्रिज्या वाली एक बेलनाकार बाल्टी रेत से पूरी भरी है। इसके रेत को जमीन पर उडेलकर एक शंकु के आकार में एकत्रित ! किया गया है। यदि इस शंक्वाकार ढेरी की ऊँचाई 24 cm हो, तो इस ढेरी की त्रिज्या एवं तिर्यक ऊँचाई ज्ञात कीजिए।

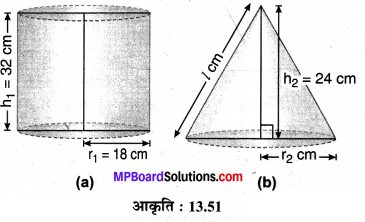
हल :
दिया है : एक बेलनाकार बाल्टी जिसकी आधार त्रिज्या r1 = 18 cm एवं ऊँचाई h1 = 32 cm जो रेत से भरी हुई है। इस रेत को जमीन पर उडेलकर एक शंक्वाकार ढेरी बनाई गई है जिसकी ऊँचाई h2 = 24 cm है। मान लीजिए ढेरी की आधार त्रिज्या r2 cm एवं तिर्यक ऊँचाई l cm है, तो प्रश्नानुसार शंक्वाकार ढेरी (रेत) का आयतन = बेलन के रेत का आयतन


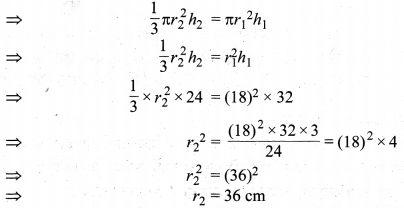
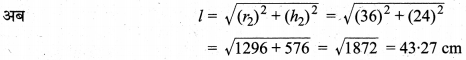
अतः, शंक्वाकार ढेरी के आधार की अभीष्ट त्रिज्या = 36 cm
एवं ढेरी की अभीष्ट तिर्यक ऊँचाई = 43.27 cm (लगभग) है।

प्रश्न 24.
एक इमारत बेलनाकार है जिसके ऊपर एक अर्द्धगोलाकार गुम्बद है तथा इसमें \(41\frac { 19 }{ 21 }\) m³ वायु (हवा) है। यदि गुम्बद का आन्तरिक व्यास इस इमारत की कुल ऊँचाई के बराबर है, तो इस इमारत की कुल ऊँचाई ज्ञात कीजिए।
हल :

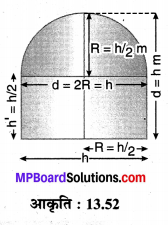
मान लीजिए कि दी हुई इमारत की कुल ऊँचाई = h है जो कि गुम्बद के व्यास के बराबर है, जो आधार के व्यास के बराबर है।
हवा का आयतन \(41\frac { 19 }{ 21 }\) m³ है। अतः बेलन की त्रिज्या = गुम्बद की त्रिज्या = R = \(\frac { h }{ 2 }\) m
तथा बेलनाकार भाग की ऊँचाई = h’ = h – h/2 = h/2 m
हवा का कुल आयतन V = बेलन का आयतन + गुम्बद का आयतन

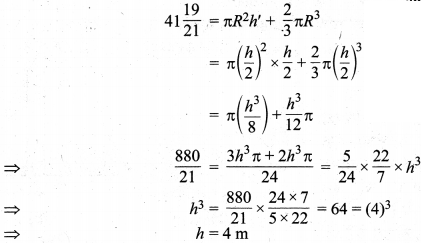
अतः, इमारत की अभीष्ट कुल ऊँचाई = 4 m है।

प्रश्न 25.
लकड़ी से बना एक कलमदान घनाभ के आकार का है जिसकी विमाएँ 10 cm x 5 cm x 4 cm हैं। इसमें चार शंक्वाकार गड्ढे पैन (कलम) रखने के लिए तथा एक घनाकार गड्ढा पिन रखने के लिए बने हैं। प्रत्येक शंक्वाकार गड्ढे की त्रिज्या 0.5 cm एवं गहराई 2.1 cm है तथा घनाकार गड्ढे की कोर 3 cm है तो सम्पूर्ण कलमदान में लगने वाली लकड़ी का आयतन ज्ञात कीजिए।
हल :
दिया है: एक 10 cm x 5 cm x 4 cm विमाओं वाला लकड़ी का बना एक घनाभ के आकार का कलमदान जिसमें 4 शंक्वाकार गड्ढे प्रत्येक की त्रिज्या r = 0.5 cm एवं गहराई h = 2.1 cm तथा एक घनाकार गड्ढा जिसकी भुजा a = 3 cm है दिए हैं। कलमदान की कुल लकड़ी का आयतन
V = 10 x 5 x 4 = 200 cm³
4 शंक्वाकार गड्ढ़ों का आयतन = 4 x \(\frac { 1 }{ 3 }\) πr²h
V₁ = 4 x \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (0.5)² x 2.1 cm³
= 2.2 cm³
एवं घनाकार गड्ढे का आयतन V₂ = a³ = (3)³ = 27 cm
प्रयुक्त लकड़ी का आयतन = V – V₁ – V₂ = 200 – 2.2 – 27
= 200 – 29.2
= 170.8 cm³
अतः, कलमदान में प्रयुक्त अभीष्ट लकड़ी का आयतन = 170.8 cm³ है।

MP Board Class 10th Maths Chapter 13 लघु उत्तरीय प्रश्न

प्रश्न 1.
8 cm त्रिज्या के लोहे के एक गोले को गलाकार 1 cm त्रिज्या के कितने गोले बनाए जा सकते है?
हल :
ज्ञात है: बड़े गोले की त्रिज्या R = 8 cm
एवं छोटे प्रत्येक गोले की त्रिज्या r = 1 cm
मान लीजिए छोटे गोलों की संख्या n है तो
n छोटे गोलों का आयतन = 1 बड़े गोले का आयतन
\(n \times \frac{4}{3} \pi r^{3}=\frac{4}{3} \pi R^{3}\)
nr³ = R³
n (1)³ = (8)³ = 512
n = 512
अतः, अभीष्ट गोलों की संख्या = 512 है।

प्रश्न 2.
तीन धातु के घन जिनकी कोरों की लम्बाई क्रमश: 5 cm, 4 cm और 3 cm है, को पिघलाकर एक नए घन में बदल दिया गया है। इस प्रकार बने नए घन की कोर क्या होगी?
हल :
माना तीन घनों की कोरें क्रमशः a₁ = 5 cm, a₂ = 4 cm एवं a₃ = 3 cm हैं, इनको गलाकर नया घन बनाया गया है और मान लीजिए इस नए घन की कोर a cm हो तो बड़े घन का आयतन
V = V₁ + V₂ + V₃
a³ = a₁³ + a₂³ + a₃³
= (5)³ + (4)³ + (3)³
= 125 + 64 + 27
= 216 cm³
a³ = (6)³
a = 6 cm
अतः, नए घन की अभीष्ट कोर की लम्बाई = 6 cm है।

प्रश्न 3.
सीसे के बने एक 9 cm x 11 cm x 12 cm विमाओं वाले ठोस घनाभ से 3 cm व्यास वाली कितनी गोलियाँ बनेंगी?
हल :
सीसे के ठोस घनाभ की विमाएँ 9 cm x 11 cm x 12 cm हैं जिसे पिघलाकर व्यास
d = 2r = 3 cm
r = \(\frac { 3 }{ 2 }\) cm त्रिज्या वाली मान लीजिए n गोलियाँ बनेंगी।
प्रश्नानुसार, n गोलियाँ का आयतन = घनाभ का आयतन

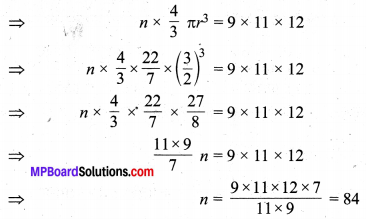
अतः, गोलियों की अभीष्ट संख्या = 84 है।

प्रश्न 4.
एक बाल्टी एक शंकु छिन्नक के आकार की है जिसके दोनों सिरों की त्रिज्याएँ क्रमश: 28 cm एवं 21 cm हैं। इसमें 28.490 लीटर पानी भरा है। बल्टी की ऊँचाई ज्ञात कीजिए।
हल :
छिन्नक के आकार की बाल्टी के सिरों की त्रिज्याएँ क्रमशः r₁ = 28 cm एवं r₂ = 21 cm हैं तथा इसकी धारिता (आयतन) V = 28.490 लीटर = 28490 cm³ । मान लीजिए कि बाल्टी की ऊँचाई = h cm है तो प्रश्नानुसार,
V = \(\frac { 1 }{ 3 }\) πh (r₁² + r₂² + r₁r₂)
= \(\frac{1}{3} \times \frac{22}{7}\) [(28)² + (21)² + (28) (21)] h = 28490
= \(\frac{1}{3} \times \frac{22}{7}\) (784 + 441 + 588) h = 28490
\(\frac{1}{3} \times \frac{22}{7} \times 1813 h\) = 28490
\(h=\frac{28490 \times 3 \times 7}{22 \times 1813}\)
h = 15 cm
अतः, छिन्नक (बाल्टी) की अभीष्ट ऊँचाई = 15 cm है।

प्रश्न 5.
7 cm भुजा वाले एक घन में एक शंक्वाकार गुहा (cavity)7 cm गहरी तथा 3 cm त्रिज्या वाली बनायी गयी है। शेष ठोस का आयतन ज्ञात कीजिए।
हल :
मान लीजिए एक घन की भुजा a = 7 cm दिया है जिसमें गहराई h = 7 cm एवं त्रिज्या r = 3 cm वाली एक शंक्वाकार गुहा बनायी गयी है।
घन का आयतन V = a³ = (7)³ = 343 cm³
शंक्वाकार गुहा का आयतन \(V_{1}=\frac{1}{3} \pi r^{2} h\)
\(V_{1}=\frac{1}{3} \times \frac{22}{7} \times(3)^{2} \times 7\)
= 66 cm³
शेष ठोस का आयतन = 343 – 66 = 277 cm³
अतः, शेष ठोस का अभीष्ट आयतन = 277 cm³ है।

प्रश्न 6.
दो सर्वांगसम शंकु जिनकी आधार त्रिज्या r = 8 cm एवं ऊँचाई h = 15 cm है। आपस में आधार के साथ जोड़ दिए गए हैं। बने संयुक्त ठोस का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :

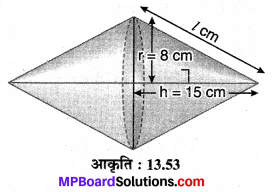
दो सर्वांगसम शंकु संलग्न आकृति के अनुसार आपस में जोड़े गए हैं। प्रत्येक शंकु की त्रिज्या r= 8 cm एवं ऊँचाई h = 15 cm है।
एक शंकु की तिर्यक ऊँचाई \(l=\sqrt{h^{2}+r^{2}}\)
[पाइथागोरस प्रमेय से]
\(l=\sqrt{(15)^{2}+(8)^{2}}=\sqrt{225+64}\)
= √289
= 17 cm
प्राप्त ठोस का सम्पूर्ण पृष्ठ = 2 x एक शंकु का वक्रपृष्ठ
S_w = 2 x πrl
= 2 x \(\frac { 22 }{ 7 }\) x 8 x 17
\(S_{w}=\frac{44 \times 8 \times 17}{7}=\frac{5984}{7}\)
= 854.86 cm² लगभग।
अतः, अभीष्ट सम्पूर्ण पृष्ठ = 854.86 cm² (लगभग) है।

प्रश्न 7.
7 cm व्यास वाले एक बीकर में कुछ पानी भरा है। इसमें 1.4cm व्यास वाले कुछ कंचे डाले जाते हैं। बीकर में डाले गए कंचों की संख्या ज्ञात कीजिए जिससे बीकर में पानी का स्तर 5.6cm चढ़ जाता है।
हल :
दिया है, व्यास d = 2r = 7 cm
r = \(\frac { 7 }{ 2 }\) = cm त्रिज्या वाले बेलनाकार बीकर में कुछ पानी है जिसमें मान लीजिए कि व्यास d₁ = 2r₁ = 1.4 cm
r = \(\frac { 1.4 }{ 2 }\) = 0.7 cm त्रिज्या वाले n गोलाकार कंचे डाले जाते हैं जिससे बीकर में जल स्तर h = 5.6 cm चढ़ जाता है, तो प्रश्नानुसार,
n कंचों का आयतन = बीकर में विस्थापित जल का आयतन

अतः, अभीष्ट कंचों की संख्या = 150 है।

प्रश्न 8.
एक 66 cm x 42 cm x 21 cm विमाओं वाले ठोस सीसे के घनाभ को पिघालकर 4.2 cm व्यास वाली कितनी सीसे की ठोस गोलियाँ प्राप्त की जा सकती हैं?
हल :
दिया है, 66 cm x 42 cm x 21 cm विमाओं वाले ठोस सीसे के घनाभ को पिघलाकार मान लीजिए n गोलियाँ बनाई जाती हैं जिनमें प्रत्येक का व्यास d = 2r = 4.2 cm अर्थात् त्रिज्या r = \(\frac { 4.2 }{ 2 }\) = 2.1 cm है तो प्रश्नानुसार,
n गोलियाँ का आयतन = घनाभ का आयतन

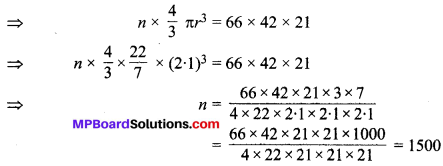
अतः, अभीष्ट गोलियों की संख्या = 1500 है।

प्रश्न 9.
सीसे के बने एवं 44 cm भुजा वाले एक ठोस धन से 4 cm व्यास वाली कितनी गोलियाँ बन सकती हैं?
हल:
दिया है, एक a = 44 cm भुजा वाला सीसे का ठोस घन जिसको पिघलाकर माना n गोलियाँ बनायी जाती हैं जिनमें प्रत्येक गोली का व्यास d = 2r = 4cm
⇒ r = \(\frac { 4 }{ 2 }\) = 2 cm अर्थात् त्रिज्या r = 2 cm दी है, तो प्रश्नानुसार,
n x गोलियाँ का आयतन = घन का आयतन


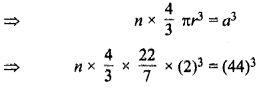
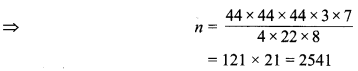
अतः, गोलियों की अभीष्ट संख्या = 2541 है।

प्रश्न 10.
एक दीवार 24 m लम्बी, 0.4 m मोटी एवं 6 m ऊँची बनानी है। इसको बनाने में 25 cm x 16 cm x 10 cm विमाओं वाली कितनी ईंटें लगेंगी जबकि दीवार के आयतन का \(\frac { 1 }{ 10 }\) भाग गारे द्वारा घेरा जायेगा?
हल :
दीवार की विमाएँ l = 24 m, b = 0.4m एवं h = 6 m तथा प्रत्येक ईंट की विमाएँ 25 cm x 16 cm x 10 cm दी हैं तथा दीवार के आयतन का \(\frac { 1 }{ 10 }\) भाग गारे द्वारा घेरा जाएगा। मान लीजिए ईंटों की संख्या n है तो
दीवार का आयतन V = lbh = 24 x 0.4 x 6 m³
V = 57.6 m³ = 57.6 x 10⁶ cm³
गारे द्वारा घेरा गया आयतन = \(\frac { 1 }{ 10 }\) V = 5.76 x 10⁶ cm³
दीवार का शेष आयतन = 57.6 x 10⁶ – 5.76 x 10⁶ cm³
= 51.84 x 10⁶ cm³
प्रश्नानुसार, n ईंटों का आयतन = शेष दीवार का आयतन
n x 25 x 16 x 10 = 51.84 x 10⁶ cm³
4 x 103 n = 51.84 x 10⁶ cm³
\(n=\frac{51 \cdot 84 \times 10^{6}}{4 \times 10^{3}}\)
n = 12.96 x 10³
= 12960 ईंटें
अतः, ईंटों की अभीष्ट संख्या = 12960 है।

प्रश्न 11.
आधार व्यास 1.5 cm एवं मोटाई (ऊँचाई) 0.2 cm वाली वृत्ताकार तस्तरियों की संख्या ज्ञात कीजिए जिनको पिघलाकर एक लम्ब वृत्तीय बेलन 4.5 cm व्यास एवं 10 cm ऊँचाई वाला बन सके।
हल :
वृत्ताकार तस्तरी का व्यास d₁ = 2r₁ = 1.5 cm = \(\frac { 3 }{ 2 }\)cm
त्रिज्या r₁ = \(\frac { 3 }{ 2 }\) cm एवं ऊँचाई (मोटाई) h₁ = 0.2 cm की संख्या n (मान लीजिए) को पिघलाकर h₂ = 10 cm ऊँचा एवं व्यास
d₂ = 2r₂ = 4.5 cm = \(\frac { 9 }{ 2 }\)
r₂ = \(\frac { 9 }{ 4 }\) cm वाला लम्ब वृत्तीय बनाया गया है, तो प्रश्नानुसार
n तस्तरियों का आयतन = बेलन का आयतन

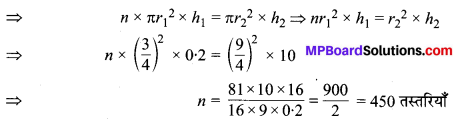
अतः, तस्तरियों की अभीष्ट संख्या = 450 है।

MP Board Class 10th Maths Chapter 13 अति लघु उत्तरीय प्रश्न

निम्न कथनों में सत्य/असत्य लिखिए एवं अपने उत्तर का औचित्य दीजिए।

प्रश्न 1.
दो सर्वांगसम एवं समान आधार त्रिज्या वाले ठोस अर्द्धगोले आधार से आधार जोड़ दिए गए हैं। उनका सम्पूर्ण पृष्ठीय क्षेत्रफल 6πr² होगा।
हल :
असत्य कथन, क्योंकि उनका सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πr² होगा वे एक गोला बनाएँगे।

प्रश्न 2.
r त्रिज्या एवं h ऊँचाई वाले एक ठोस बेलन को समान ऊँचाई एवं त्रिज्या वाले बेलन पर रखा जाता है तो इस प्रकार प्राप्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πrh + 4πr² होगा।
हल :
कथन असत्य है, क्योंकि प्राप्त ठोस एक 2h ऊँचाई एवं r त्रिज्या का बेलन होगा और उसका सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πrh + 2πr² होगा।

प्रश्न 3.
h ऊँचाई एवं r त्रिज्या वाला एक ठोस शंकु एकसमान आधार त्रिज्या एवं समान ऊँचाई वाले बेलन पर रखा है। संयुक्त ठोस का कुल पृष्ठीय क्षेत्रफल है \(\pi r[\sqrt{r^{2}+h^{2}}+3 r+2 h]\).
हल :
कथन असत्य है, क्योंकि संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल \(\pi r[\sqrt{r^{2}+h^{2}}+r+2 h]\) होगा।

प्रश्न 4.
एक ठोस बॉल ठीक प्रकार एक a भुजा वाले घन के अन्दर रखी है तो बॉल का आयतन \(\frac{4}{3} \pi a^{3}\) होगा।
हल :
कथन असत्य है, क्योंकि बॉल का आयतन = \(\frac{1}{6} \pi a^{3}\) होगा।

प्रश्न 5.
एक शंकु के छिन्नक का आयतन \(\frac{1}{3} \pi h\left[r_{1}^{2}+r_{2}^{2}-r_{1} r_{2}\right]\) है, जहाँ h छिन्नक की ऊर्ध्वाधर ऊँचाई तथा r1, r2 उसके सिरों की त्रिज्याएँ हैं।
हल :
कथन असत्य है, क्योंकि छिन्नक का आयतन =\(\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\) होता है।

प्रश्न 6.
एक बेलनाकार बर्तन में नीचे अन्दर की ओर एकसमान त्रिज्या का अर्द्ध गोलीय उभार है। इस बर्तन की ऊँचाई h एवं त्रिज्या r है उसकी धारिता है \(\frac{\pi r^{2}}{3}(3 h-2 r)\) है। हल :
कथन सत्य है, क्योंकि बर्तन की धारिता = बेलन का आयतन – अर्द्धगोले का आयतन
= \(\pi r^{2} h-\frac{2}{3} \pi r^{3}=\frac{\pi r^{2}}{3}(3 h-2 r)\) होगा।

प्रश्न 7.
एक शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल \(\pi l\left(r_{1}+r_{2}\right)\) है, जहाँ \(l=\sqrt{h^{2}+\left(r_{1}+r_{2}\right)^{2}}\) एवं r1 तथा r2 क्रमशः दोनों सिरों की त्रिज्याएँ।
हल :
कथन असत्य है, क्योंकि वक्र पृष्ठीय क्षेत्रफल तो \(\pi l\left(r_{1}+r_{2}\right)\) होगा लेकिन \(l=\sqrt{(h)^{2}+\left(r_{1}-r_{2}\right)^{2}}\) होगा, जहाँ r1, r2 क्रमशः सिरों की त्रिज्याएँ हैं।

प्रश्न 8.
एक धातु की खुली बाल्टी जो एक शंकु के छिन्नक के आकार की है, एक खोखले बेलनाकार आधार पर टिकी है जो उसी धातु का बना है। धातु की प्रयुक्त चद्दर का क्षेत्रफल बराबर है छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल।
हल :
कथन सत्य है, क्योंकि बाल्टी का सम्पूर्ण पृष्ठीय क्षेत्रफल इन क्षेत्रफलों से मिलकर बना है।

प्रश्न 9.
एक ठोस शंकु अपने समान ऊँचाई h एवं त्रिज्या r वाले बेलन पर रखा है तो संयुक्त ठोस का वक्र पृष्ठीय क्षेत्रफल \(\pi r \sqrt{h^{2}+r^{2}}+2 \pi r h\) है।
हल :
कथन सत्य है, क्योंकि संयुक्त ठोस का बक्रपृष्ठीय क्षेत्रफल बेलन के वक्रपृष्ठीय क्षेत्रफल 2πrh एवं शंकु के वक्रपृष्ठीय क्षेत्रफल πrl अर्थात \(\pi r \sqrt{h^{2}+r^{2}}\) के योग के बराबर होगा।

प्रश्न 10.
एक स्टील की गोलाकार बॉल पिघलाकार 8 नए सर्वांगसम बॉलों में ढाली गयी है तो प्रत्येक बॉल की त्रिज्या मूल बॉल की त्रिज्या का \(\frac { 1 }{ 8 }\) भाग होगा।
हल :
कथन असत्य है, क्योंकि उसकी त्रिज्या मूल त्रिज्या की \(\frac { 1 }{ 2 }\) होगी।

प्रश्न 11.
दो सर्वांगसम घन जिनमें प्रत्येक की भुजा a हो आपस में जोड़े गए हैं, तो कुल पृष्ठीय क्षेत्रफल 12a² है।
हल :
कथन असत्य है, क्योंकि कुल पृष्ठीय क्षेत्रफल 10a² होगा।

MP Board Class 10th Maths Chapter 13 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 13 बहु-विकल्पीय प्रश्न

प्रश्न 1.
संलग्न आकृति एक फनल की है जो एक संयुक्त आकृति है :

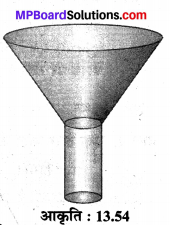
(a) एक शंकु एवं एक बेलन की
(b) एक शंकु छिन्नक एवं एक बेलन की
(c) एक अर्द्ध गोला एवं एक बेलन की
(d) एक अर्द्ध गोला एवं एक शंकु की।
उत्तर:
(b) एक शंकु छिन्नक एवं एक बेलन की

प्रश्न 2.
एक शंकु छिन्नक के सिरों की त्रिज्याएँ क्रमशः r1 cm एवं r2 cm तथा ऊँचाई h cm है तो आयतन cm³ में होगा :

उत्तर:
(a) \(\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\)

प्रश्न 3.
एक सिरे पर छीली गई एक बेलनाकार पेन्सिल एक संयुक्त आकृति है:

(a) एक बेलन एवं एक शंकु की
(b) एक शंकु छिन्नक एवं एक बेलन की
(c) एक अर्द्ध गोला एवं एक बेलन की
(d) दो बेलनों की।
उत्तर:
(a) एक बेलन एवं एक शंकु की

प्रश्न 4.
एक सुराही संयुक्त आकृति है :

(a) एक गोले एवं एक बेलन की
(b) एक अर्द्ध गोला एवं एक बेलन की
(c) दो अर्द्ध गोलों की
(d) एक बेलन एवं एक शंकु की।
उत्तर:
(a) एक गोले एवं एक बेलन की

प्रश्न 5.
एक साहुल सूत्र (प्लम्ब लाइन) (देखिए संलग्न आकृति) एक संयुक्त आकृति है:

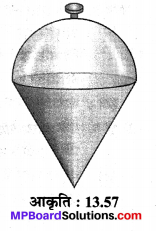
(a) एक शंकु एवं एक बेलन की
(b) एक अर्द्ध गोला एवं एक शंकु की
(c) एक शंकु छिन्नक एवं एक बेलन की
(d) एक गोला एवं एक बेलन की।
उत्तर:
(b) एक अर्द्ध गोला एवं एक शंकु की

प्रश्न 6.
एक गिलास प्रायः निम्न आकृति का होता है :

(a) एक शंकु की
(b) एक शंकु छिन्नक की
(c) एक बेलन की
(d) एक गोले की।
उत्तर:
(b) एक शंकु छिन्नक की

प्रश्न 7.
गिल्ली-डंडा खेल की गिल्ली संयुक्त आकृति होती है निम्न की :

(a) दो बेलनों की
(b) एक शंकु एवं एक बेलन की
(c) दो शंकु एवं एक बेलन की
(d) दो बेलन एवं एक शंकु की।
उत्तर:
(c) दो शंकु एवं एक बेलन की

प्रश्न 8.
बैडमिण्टन खेल में प्रयुक्त एक शटल कॉक एक संयुक्त आकृति

(a) एक बेलन एवं एक गोला की
(b) एक बेलन एवं एक अर्द्ध गोला की
(c) एक गोला एवं एक शंकु की
(d) एक शंकु-छिन्नक एवं एक अर्द्ध गोला की।
उत्तर:
(d) एक शंकु-छिन्नक एवं एक अर्द्ध गोला की।

प्रश्न 9.
एक शंक को उसके आधार के समान्तर एक तल द्वारा काटने पर एक सिरे पर प्राप्त छोटे शंकु को पृथक् कर दिया जाता है। इस प्रकार शेष बचा ठोस कहलाता है:
(a) एक शंकु का एक छिन्नक
(b) शंकु
(c) बेलन
(d) गोला।
उत्तर:
(a) एक शंकु का एक छिन्नक

प्रश्न 10.
एक ठोस 2 cm व्यास एवं 16 cm ऊँचाई वाले बेलन को पिघलाकर 12 सर्वांगसम गोले बनाए जाते हैं तो प्रत्येक गोले का व्यास होगा :
(a) 4 cm
(b) 3 cm
(c) 2 cm
(d) 6 cm.
उत्तर:
(c) 2 cm

प्रश्न 11.
यदि दो ठोस समान आधार त्रिज्या के r अर्द्ध गोले आपस में आधार से आधार सटाकर जोड़ दिए जाते हैं तो इस प्रकार प्राप्त नए ठोस का वक्र पृष्ठीय क्षेत्रफल होगा :
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
उत्तर:
(a) 4πr²

प्रश्न 12.
r cm त्रिज्या एवं h cm (h > 2r) ऊँचाई का एक लम्ब वृत्तीय बेलन एक गोले को ठीक-ठीक ढक लेता है तो इस गोले का व्यास होगा :
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm.
उत्तर:
(b) 2r cm

प्रश्न 13.
एक ठोस को दूसरे ठोस में परिवर्तित करने पर नए ठोस का आयतन :
(a) बढ़ जायेगा
(b) घट जायेगा
(c) अपरिवर्तित रहेगा
(d) दूना होगा।
उत्तर:
(c) अपरिवर्तित रहेगा

प्रश्न 14.
एक लम्बवृत्तीय शंकु को आधार के समान्तर तल द्वारा काटने पर प्राप्त परिच्छेद होगा :
(a) वृत्त
(b) शंकु छिन्नक
(c) गोला
(d) अर्द्ध गोला।
उत्तर:
(a) वृत्त

प्रश्न 15.
दो गोलों के आयतनों का अनुपात 64 : 27 है तो उनके पृष्ठीय क्षेत्रफलों का अनुपात होगा :
(a) 3:4
(b) 4:3
(c) 9:16
(d) 16:9.
उत्तर:
(d) 16:9.

रिक्त स्थानों की पूर्ति

1. किसी शंकु को उसके आधार के समान्तर तल द्वारा काटकर छोटे शंकु को हटाने पर शेष बचा ठोस …………. कहलाता है।
2. शंकु छिन्नक के दोनों सिरे …………. होते हैं।
3. बाल्टी का आकार प्रायः एक …………. का होता है।
4. शंकु छिन्नक का आयतन दोनों शंकुओं के आयतनों के …………. के बराबर होता है।
5. शंकु छिन्नक का वक्र पृष्ठीय क्षेत्रफल दोनों शंकुओं के वक्र प्रष्ठीय क्षेत्रफलों के …………. के बराबर होता है।
उत्तर-
1.शंकु छिन्नक,
2. वृत्ताकार,
3. शंकु छिन्नक,
4. अन्तर,
5. अन्तर।

जोड़ी मिलाइए

उत्तर-
1.→(b),
2.→(c),
3.→(a).

सत्य/असत्य कथन

1. शंकु छिन्नक का आयतन संगत शंकुओं के आयतनों के योग के बराबर होता है।
2. यदि किसी बेलन के एक सिरे पर उसी त्रिज्या का एक अर्द्ध गोलाकार गड्ढा कर दिया जाए तो प्राप्त ठोस का वक्र पृष्ठीय क्षेत्रफल दोनों के वक्र पृष्ठीय क्षेत्रफल के योग के बराबर होता है। 3. शंकु छिन्नक का वक्रपृष्ठीय क्षेत्रफल संगत शंकुओं के वक्र पृष्ठीय क्षेत्रफलों के योग के बराबर होता है।
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य।

एक शब्द/वाक्य में उत्तर

1. एक शंकु छिन्नक जिसके सिरों की त्रिज्याएँ क्रमशः r₁ एवं r₂ तथा तिर्यक ऊँचाई l तो उसका सम्पूर्ण पृष्ठीय क्षेत्रफल क्या होगा?
2. शंकु के छिन्नक के आयतन का सूत्र लिखिए। (2019)
उत्तर-
1. S_w = πl (r₁ + r₂) + πr₁² + πr₂²
2. V = \(\frac { 1 }{ 3 }\)πh(r₁² + r₂² + r₁r₂).