MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.4
Question 1.
Amina thinks of a number and subtracts \(\frac{5}{2}\) from it. She multiplies the result by 8.
The result now obtained is 3 times the same number she thought of. What is the number?
Solution:
Let the number be x.
After subtracting \(\frac{5}{2}\) from x and multiplying the result by 8, we get \(\left(x-\frac{5}{2}\right) \times 8\)

⇒ (2x – 5) × 4 = 3x ⇒ 8x – 20 = 3x
⇒ 8x – 3x = 20 ⇒ 5x = 20 ⇒ x = 4
∴ The number that Amina thought of is 4.
![]()
Question 2.
A positive number is 5 times another number. If 21 is added to both the numbers, then one of the new numbers becomes twice the other new number. What are the numbers?
Solution:
Let one number be x.
∴ Another number be 5x.
Now, according to question,
2(x + 21) = 5x + 21 ⇒ 2x + 42 = 5x + 21
⇒ 42 – 21 = 5x – 2x ⇒ 21 = 3x
![]()
∴ One number is 7 and another number is 5 × 7 = 35.
![]()
Question 3.
Sum of the digits of a two-digit number is 9. When we interchange the digits, it is found that the resulting new number is greater than the original number by 27. What is the two-digit number?
Solution:
Let the digit at the units place be x.
∴The digit at the tens place be 9 – x.
⇒ The given two-digit number is
10 × (9 – x) + x = 90 – 10x + x = 90 – 9x
After interchanging the digits, we get a new number i.e., 10 × x + (9 – x) = 10x + 9 – x = 9x + 9
Now, according to question,
9x + 9 – (90 – 9x) = 27 ⇒ 9x + 9 – 90 + 9x = 27
⇒ 18x – 81 = 27 ⇒ 18x = 27 + 81
![]()
The units digit is 6 and tens digit is 9 – 6 = 3
∴ The required two-digit number is 36.
Question 4.
One of the two digits of a two digit number is three times the other digit. If you interchange the digits of this number and add the resulting number to the original number, you get 88. What is the original number?
Solution:
Let the digit at units place be x and the digit at tens place be 3x.
∴ The given number is 10 × 3x + x = 30x + x
= 31 x
After interchanging the digits, we get a new number i.e., 10 × x + 3x = 10x + 3x = 13x
Now, according to question,
31x + 13x = 88
⇒ 44x = 88 ⇒ x = 2
∴ The digit at units place is 2 and the digit at tens place is 3 × 2 = 6.
Thus, the required number is 62 or 26.
![]()
Question 5.
Shobo’s mother’s present age is six times Shobo’s present age. Shobo’s age five years from now will be one third of his mother’s present age. What are their present ages?
Solution:
Let Shobo’s present age be x years
∴ Shobo’s mother’s present age = 6x years
After 5 years,
Shobo’s age = (x + 5) years
According to question,
![]()
⇒ x + 5 = 2x
⇒ 5 = 2x – x ⇒ 5 = x
∴ Shobo’s present age is 5 years and Shobo’s mother’s present age is 6 × 5 = 30 years.
Question 6.
There is a narrow rectangular plot, reserved for a school, in Mahuli village. The length and breadth of the plot are in the ratio 11 : 4. At the rate ₹ 100 per metre it will cost the village panchayat ₹ 75000 to fence the plot. What are the dimensions of the plot?
Solution:
Since, length and breadth are in the ratio 11 : 4. So, let length is 11x and breadth is4x.
Now, perimeter of the plot

Perimeter of rectangular plot = 2 (length + breadth) = 2 (11x + 4x) = 2 × 15x = 30x
⇒ 30x = 750 ⇒ x = \(\frac{750}{30}\) = 25
∴ Length of the plot = 11x = 11 × 25 = 275 m and breadth of the plot = 4x = 4 × 25 = 100 m
Question 7.
Hasan buys two kinds of cloth materials for school uniforms, shirt material that costs him ₹ 50 per metre and trouser material that costs him ₹ 90 per metre. For every 2 metres of the trouser material he buys 3 metres of the shirt material. He sells the materials at 12% and 10% profit respectively. His total sale is ₹ 36,660. How much trouser material did he buy?
Solution:
Let material bought for trousers = 2x metres
and material bought for shirts = 3x metres
Cost of material bought for shirts = ₹ 50 × 3x
= ₹ 150x
and cost of material bought for trousers
= ₹ 90 × 2x = ₹ 180x
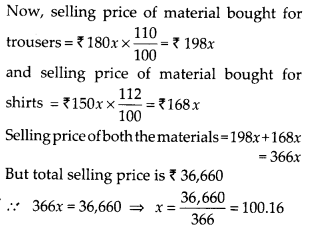
Thus, material bought for trousers = 2x m
= 2 × 100.16 m
= 200.32 m
![]()
Question 8.
Half of a herd of deer are grazing in the field and three fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Solution:
Let number of deer in the herd be x.

Therefore, number of deer in the herd is 72.
Question 9.
A grandfather is ten times older than his granddaughter. He is also 54 years older than her. Find their present ages.
Solution:
Let granddaughter’s present age be x years.
Grandfather’s present age = 10x years …(i)
Also, grandfather’s age = (x + 54) years …(ii)
From (i) and (ii), we get x + 54 = 10x
⇒ 54 = 10x – x ⇒ 54 = 9x ⇒ 6 = x
∴ Granddaughter’s present age = 6 years and grandfather’s present age = 10 × 6
= 60 years
![]()
Question 10.
Aman’s age is three times his son’s age. Ten years ago he was five times his son’s age. Find their present ages.
Solution:
Let the present age of Aman’s son be x years.
∴ The present age of Aman = 3x years
10 years ago,
Aman’s son’s age = (x -10) years and Aman’s age = (3x – 10) years
Now, according to question,
3x – 10 = 5(x -10) ⇒ 3x – 10 = 5x – 50
⇒ 50 – 10 = 5x – 3x ⇒ 40 = 2x
⇒ 20 = x
Thus, Aman’s present age = 3 × 20 = 60 years and his son’s age = 20 years