MP Board Class 8th Maths Solutions Chapter 11 Mensuration Ex 11.1
Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
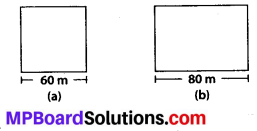
Solution:
We have, a square of side 60 m
i. e., s = 60 m and a rectangle of length a = 80 m
Perimeter of square = 4 × s = 4 × 60m = 240 m
As given, the perimeter of square and rectangle are equal.
Let, b be the other side of a rectangle.
∴ 2 × a + 2 × b = 240 m
⇒ 2 × 80 + 2 × 6 = 240
⇒ 2 × b = 240 – 160 ⇒ 2 × b = 80 m
⇒ b = 40 m
Hence, area of a square = s2 = 60 m × 60 m
= 3600 sq. m
Area of rectangle = a × 6 = 80m × 40m
= 3200 sq. m .
Hence, area of a square is larger than that of the rectangle.
![]()
Question 2.
Mrs. Kaushik has a square plot with the measurement as shown in figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m2.
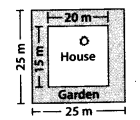
Solution:
The dimensions of the plot and house are as shown
∴ The area of plot = 25 × 25 = 625 sq. m
and the area of house = 20 × 15 = 300 sq. m
We know, Area of plot = Area of house + Area of garden
∴ Area of garden = Area of plot – Area of house
= 625 – 300 = 325 sq. m
We also know,
Rate of developing 1 sq. m garden = 55
∴ Amount for developing 325 sq. m garden = 325 × 55= 17875.
![]()
Question 3.
The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of this garden (Length of rectangle is 20 – (3.5 + 3.5) metres).
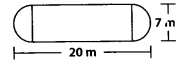
Solution:
1 Length of rectangle = 20 – radii of semicircles (20 – (3.5 + 3.5)) m = 13 m.
Hence area of garden = Area of rectangle + Area of 2 semi circles
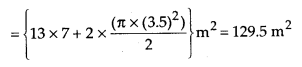
Perimeter of garden = πr +2 × (l) + πr
= 2(l + πr)
=2(13 + π × 3.5)m = 48m.
Question 4.
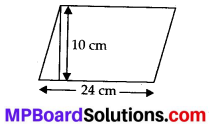
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2?
(If required you can split the tiles in whatever way you want to fill up the corners).
Solution:
The base of tile (b) = 24 cm and height h = 10 cm
∴ Area of 1 tile = 24 × 10 sq. cm
= 240 sq. cm.
Thus, to cover an area of 1080 m2, we need number of tiles
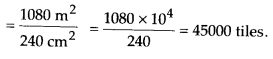
![]()
Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.
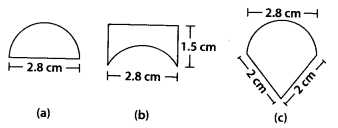
Solution:
The circumference of a circle is given by 2πr and perimeter of a semicircle is given by πr + 2r

Perimeter = πr + 2l
= [π × 1.4 + 2 × 2] cm = 8.4 cm
Hence, the ant has to take the longest round around the piece of figure (b).