MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.3

Question 1.
Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution:
Since, we know that a polyhedron have 4 or more than 4 faces.
(i) No, it does not form a polyhedron.
(ii) Yes, since it forms a triangular pyramid.
(iii) Yes, since it forms a square pyramid.

Question 2.
Is it possible to have a polyhedron with any given number of faces? (Hint: Think of a pyramid).
Solution:
Yes, it is possible, but only if the number of faces are greater than or equal to 4.

Question 3.
Which are prisms among the following?
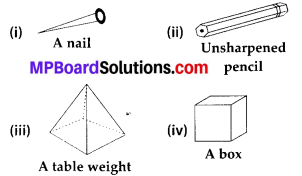
MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.3 1
Solution:
Since, we know that a prism is a polyhedron, two of whose faces are congruent polygons in parallel planes and whose other faces are parallelograms.
Only (ii) and (iv) are prisms.

Question 4.
(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Solution:
(i) A prism becomes a cylinder as the number of sides of its base becomes larger and larger.
(ii) A pyramid becomes a cone as the number of sides of its base becomes larger and larger.

Question 5.
Is a square prism same as a cube? Explain.
Solution:
No, because a square prism can be a cuboid also.

Question 6.
Verify Euler’s formula for these solids.
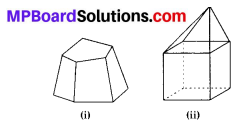
MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.3 2
Solution:
(i) Clearly, number of faces (F) = 7,
Number of edges (E) = 15,
Number of vertices (V) = 10
Now, F + V = 7 + 10 = 17 …(1)
Also, E + 2 = 15 + 2 = 17 …(2)
From (1) and (2), F + V = E + 2
∴ Euler’s formula is verified.

(ii) Clearly, number of faces (F) = 9
Number of edges (E) = 16
Number of vertices (V) = 9
Now, F + V = 9 + 9 = 18 …(1)
Also, E + 2 = 16 + 2 = 18 …(2)
From (1) and (2),
F + V = E + 2
∴ Euler’s formula is verified.

Question 7.
Using Euler’s formula find the unknown.
MP Board Class 8th Maths Solutions Chapter 10 Visualizing Solid Shapes Ex 10.3 3
Solution:
By using Euler’s formula,
F + V= E + 2,
where F ➝ Number of faces
V ➝ Number of vertices
E —> Number of edges
For 1^st Column:
F + 6 = 12 + 2
⇒ F + 6 = 14 ⇒ F = 14 – 6 = 8
Thus, the required number of faces = 8
For 2^nd Column:
5 + V = 9 + 2
⇒ 5 + V = 11
⇒ V = 11 – 5 = 6
Thus, the required number of vertices = 6
For 3^rd Column:
20 + 12 = E + 2 ⇒ 32 – 2 = E
⇒ E = 30
Thus, the required number of edges = 30

Question 8.
Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution:
We have given,
Number of faces = 10
Number of vertices = 15
Number of edges = 20
So, F + V = 10 + 15 = 25 …(i)
and E + 2 = 20 + 2 = 22 …(ii)
From (i) and (ii), we observe that
F + V ≠ E + 2 (∵ 25 ≠ 22)
Thus, there is no polyhedron with 10 faces, 20 edges and 15 vertices.