MP Board Class 8th Maths Solutions Chapter 1 Rational Numbers Ex 1.2

MP Board Class 8th Maths Solutions Chapter 1 Rational Numbers Ex 1.2

Question 1.
Represent these numbers on the number line.
(i) \(\frac{7}{4}\)
(ii) \(\frac{-5}{6}\)
Solution:
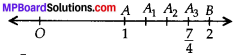
(i) We have to represent \(\frac{7}{4}\) on the number line. \(\frac{7}{4}\) can be written as \(1 \frac{3}{4} \cdot 1 \frac{3}{4}\) lies between 1 and 2.
Step-1: Draw a number line and mark O on it to represents ‘0’ (zero)
Step-2 : Take a point A to represent
1 and B to represent 2.
Step-3 : Divide the distance of A and B in four equal parts A A₁, A₁A₂, A₂A₃, A₃B.
Step-4 : Count from 1 and reach to the third point A₃ and A₃ is the required point on number line.

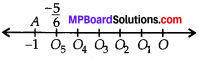
(ii) \(\frac{-5}{6}\) is lies between 0 and -1.
Step-1: Draw a number line and mark O on it to represent ‘0’ (zero).
Step-2 : Take a point A to represent -1.
Step-3 : Divide the distance of A and O in six equal parts AO₅, O₅O₄, O₄O₃, O₃O₂, O₂O₁, O₁O.
Step-4 : Count from 0 and reach to the fifth point O₅.
O₅ is the required point.

Question 2.
Represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the number line.
Solution:
We have to mark \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the same number line.
Since \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) all are less than 0 but greater than -1.
∴ All these lie between 0 and -1.

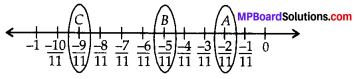
Thus, A, B and C are the required points.

Question 3.
Write five rational numbers which are smaller than 2.
Solution:
Five numbers less than 2 lies on the left of 2 on the number line.
∴ Five rational numbers are \(0, \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\)

Question 4.
Find ten rational numbers between \(\frac{-2}{5}\) and \(\frac{1}{2}\).
Solution:
We have given, two rational numbers \(\frac{-2}{5}\) and \(\frac{1}{2}\).
First we make the same denominator of both rational numbers.

Now, we have to find 10 rational numbers between \(\frac{-4}{10}\) and \(\frac{5}{10}\). so we have to multiply the numerator and denominator by a number such that difference between numerators is atleast 10.

Question 5.
Find five rational numbers between

Solution:
First we make the same denominator of both rational numbers

Since, we have to find five rational numbers between \(\frac{10}{15}\) and \(\frac{12}{15}\) so we multiply the numerator and denominator by a number such that difference between the numerators is atleast 5.

∴ The five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\) are \(\frac{41}{60}, \frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}\)

(ii) First we make the same denominator of both rational numbers.

Since, we have to find five rational numbers between and \(-\frac{9}{6}\) and \(\frac{10}{6}\), so we do not need to multiply the numerator and denominator of \(-\frac{9}{6}\) and \(\frac{10}{6}\) by any number, because we can see that the difference between the numerators is 19 > 5.
∴ Five rational numbers between \(\frac{-3}{2}\) and \(\frac{5}{3}\) are \(\frac{-8}{6}, \frac{-7}{6}, \frac{0}{6}, \frac{1}{6}, \frac{2}{6}\)

(iii) First we make the same denominator of both rational numbers.

Since we have to find five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\), so we multiply the numerator and denominator by a number such that difference between the numerators is atleast 5.

∴ Five rational numbers between \(\frac{1}{4}\) and \(\frac{2}{4}\) are \(\frac{9}{32}, \frac{10}{32}, \frac{11}{32}, \frac{12}{32}, \frac{13}{32}\).

Question 6.
Write five rational numbers greater than -2.
Solution:
Five rational numbers greater than -2 lies on the right side of -2 on number line.
∴ Any five rationals on the right of -2 are \(\frac{-3}{2},-1, \frac{-1}{2}, 0, \frac{1}{2}\).

Question 7.
Find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\)
Solution:
Make the common denominator.

Since we have to find ten rational numbers between \(\frac{3}{5}\) and \(\frac{3}{4}\) so, we multiply the numerator and denominator by a number such that difference between the numerators is atleast 10.

MP Board Class 8th Maths Solutions