MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3

Question 1.
Name any two figures have both line symmetry and rotational symmetry.
Solution:
An equilateral triangle and regular hexagon have both line symmetry and rotational symmetry.

Question 2.
Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Solution:
(i) An equilateral triangle has 3 lines of symmetry and rotational symmetry of order 3.
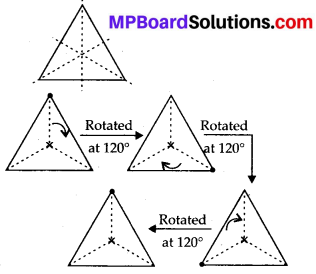
MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3 1

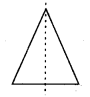
(ii) An isosceles triangle has only 1 line of symmetry and no rotational symmetry of order more than 1.
MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3 2

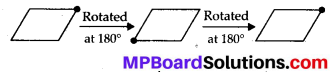
(iii) A parallelogram is a quadrilateral which has no line symmetry but a rotational symmetry of order 2.
MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3 3

(iv) A kite is a quadrilateral which has only 1 line of symmetry and no rotational- symmetry of order more than 1.
MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3 4

Question 3.
If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1 ?
Solution:
Yes, if a figure has two or more lines of symmetry, then it will definitely have its rotational symmetry of order more than 1.

Question 4.
Fill in the blanks:
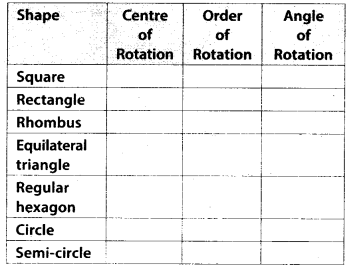
MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.3 5
Solution:
The given table can be completed as follows:

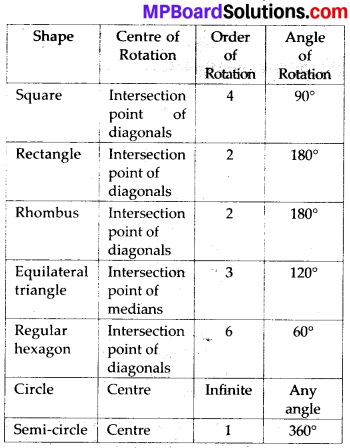
Question 5.
Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Solution:
Square, rectangle, and rhombus are the quadrilaterals which have both line and rotational symmetry of order more than 1. A square has 4 lines of symmetry and rotational symmetry of order 4. A rectangle has 2 lines of symmetry and rotational symmetry of order 2. A rhombus has 2 lines of symmetry and rotational symmetry of order 2.

Question 6.
After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Solution:
It can be observed that if a figure looks symmetrical on rotating by 60°, then it will also look symmetrical on rotating by 120°, 180°, 240°, 300°, 360° i.e., further multiples of 60°.

Question 7.
Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Solution:
It can be observed that if the angle of rotation of a figure is a factor of 360°, then it will have a rotational symmetry of order more than 1.
(i) It can be checked that 45° is a factor of 360°. Therefore, the figure having its angle of rotation as 45° will have its rotational symmetry of order more than 1.
(ii) 17° is not a factor of 360°. Therefore, the figure having its angle of rotation as 17° will not be having its rotational symmetry of order more than 1.