MP Board Class 7th Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.1
प्रश्न 1.
एक आयताकार भूखण्ड की लम्बाई और चौड़ाई क्रमशः 500 m तथा 300 m है। ज्ञात कीजिए :
(i) भूखण्ड का क्षेत्रफल
(ii) भूखण्ड का मूल्य, यदि 1 m2 का मूल्य ₹ 10,000
हल:
(i) भूखण्ड की लम्बाई, l = 500 m,
चौड़ाई b = 300 m
भूखण्ड का क्षेत्रफल = l × b
= 500 m × 300 m = 1,50,000 m2
(ii) भूखण्ड के 1 m2 का मूल्य = ₹10,000
∴ भूखण्ड के 1,50,000 m2 का मूल्य
= ₹ 10,000 × 1,50,000
= ₹ 1,50,00,00,000
![]()
प्रश्न 2.
एक वर्गाकार पार्क का क्षेत्रफल ज्ञात कीजिए जिसका परिमाप 320 m है।
हल:
∵ वर्गाकार पार्क का परिमाप = 320 m
अर्थात् 4 × भुजा = 320 m
भुजा = \(\frac { 320 }{ 4 } \)m = 80m
वर्गाकार पार्क का क्षेत्रफल = (भुजा)2
= 80 m × 80 m
= 6,400 m2
प्रश्न 3.
एक आयताकार भूखण्ड की चौड़ाई ज्ञात कीजिए यदि इसका क्षेत्रफल 440 m- और लम्बाई 22 m हो। इसका परिमाप भी ज्ञात कीजिए।
हल:
आयताकार भूखण्ड की लम्बाई = 22 m
माना कि भूखण्ड की चौड़ाई = b
∴ भूखण्ड का क्षेत्रफल = l × b = 22 × b
या 22 × b = 440
या b = \(\frac { 440 }{ 22 } \) = 20 m
अतः भूखण्ड की चौड़ाई = 20 m
परिमाप = 2(l + b)
= 2 × (22 + 20)
= 2 × 42 = 84 m
प्रश्न 4.
एक आयताकार शीट का परिमाप 100 cm है। यदि लम्बाई 35 cm हो, तो इसकी चौड़ाई ज्ञात कीजिए। क्षेत्रफल भी ज्ञात कीजिए।
हल:
आयताकार शीट का परिमाप = 100 cm, लम्बाई = 35 cm, चौड़ाई b = ?
∴ 2(l + b) = 100 cm
या 2(35 + b) = 100 cm
या 35 + b = \(\frac { 100 }{ 2 } \) = 50 cm
b = 50 – 35 = 15 cm
∴ शीट की चौड़ाई = 15 cm
अब, क्षेत्रफल = l × b
∴ शीट का क्षेत्रफल = 35 × 15 = 525 cm2
प्रश्न 5.
एक वर्गाकार पार्क का क्षेत्रफल एक आयताकार पार्क के बराबर है। यदि वर्गाकार पार्क की एक भुजा 60 m हो और आयताकार पार्क की लम्बाई 90 m हो, तो आयताकार पार्क की चौड़ाई ज्ञात कीजिए।
हल:
वर्गाकार पार्क की भुजा = 60 m
आयताकार पार्क की लम्बाई = 90 m
∴ वर्गाकार पार्क का क्षेत्रफल = a2 = 60 m × 60 m
= 3,600 m2
∵ आयताकार पार्क का क्षेत्रफल = वर्गाकार पार्क का क्षेत्रफल
∴ लम्बाई × चौड़ाई = 3,600 m2

![]()
प्रश्न 6.
एक तार आयत के आकार का है। इसकी लम्बाई 40 cm और चौड़ाई 22 cm है। यदि उसी तार को दुबारा मोड़कर एक वर्ग बनाया जाता है, तो प्रत्येक भुजा की माप क्या होगी? यह भी ज्ञात कीजिए कि किस आकार का क्षेत्रफल अधिक होगा?
हल:
लम्बाई l = 40 cm, चौड़ाई b = 22 m
परिमाप = 2(l + b)
= 2(40 + 22)
= 2 × 62 = 124cm
आयत का क्षेत्रफल = l × b
= 40 × 22
= 880 cm2
∵ तार को मोड़कर वर्ग बनाया गया है।
∴ वर्ग का परिमाप – आयत का परिमाप
4 × a= 124 cm
या वर्ग की प्रत्येक भुजा की लम्बाई a = \(\frac { 124 }{ 4 } \) = 31 cm
वर्ग का क्षेत्रफल = (a)2
= 31 × 31
= 961 cm2
∵ 961 cm2 > 880 cm2
∴ वर्ग का क्षेत्रफल आयत के क्षेत्रफल से अधिक है।
प्रश्न 7.
एक आयत का परिमाप 130 cm है। यदि आयत की चौड़ाई 30 cm हो, तो आयत की लाबाई ज्ञात कीजिए। आयत का क्षेत्रफल भी ज्ञात कीजिए।
हल:
आयत का परिमाप = 130 cm
आयत की चौड़ाई = 30 cm
∵ आयत का परिमाप = 2 × (l + b)
∴ 2(l + 30) = 130 cm
या l + 30 = \(\frac { 130 }{ 2 } \) = 65 cm
या आयत की लम्बाई l = 65 – 30 = 35 cm
∴ आयत का क्षेत्रफल = l × b
= 35 × 30 cm2
= 1,050 cm2
प्रश्न 8.
2 m लम्बाई और 1 m चौड़ाई वाले दरवाजे को एक दीवार में लगाया जाता है। दीवार की लम्बाई 4.50 m तथा चौड़ाई 3.6m है (चित्र 11.5)।₹ 20 प्रति m’ की दर से दीवार पर सफेदी (white wash) कराने का व्यय ज्ञात कीजिए।

हल:
दरवाजे की लम्बाई = 2 m, चौड़ाई = 1 m, दीवार की लम्बाई = 4.50 m, चौड़ाई = 3.6 m.
∴ दीवार का क्षेत्रफल = l × b
= 4.50 m × 3.6m
= 16.2 m2
दरवाजे का क्षेत्रफल = 2 m × 1 m = 2 m2
दीवार पर सफेदी वाला क्षेत्रफल
= दीवार का क्षेत्रफल – दरवाजे का क्षेत्रफल
= 16.2 m2 – 2 m2 = 14.2 m2
∴ सफेदी कराने का व्यय = ₹ 14.2 × 20
= ₹ 284
प्रश्न:
08 cm और 5 cm भुजाओं वाला एक आयत लीजिए। आयत को विकर्ण के अनुदिश ऐसा काटिए जिससे दो त्रिभुज प्राप्त हों (चित्र 11.6)।
एक त्रिभुज को दूसरे पर रखिए।
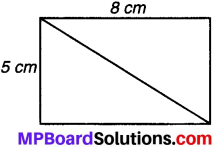
प्रश्न 1.
क्या ये दोनों पूर्णतया समान माप के हैं ?
उत्तर:
हाँ, ये दोनों पूर्णतया समान माप के हैं।
प्रश्न 2.
क्या आप कह सकते हैं कि दोनों त्रिभुजों का क्षेत्रफल बराबर है ?
उत्तर:
हाँ, दोनों त्रिभुजों का क्षेत्रफल बराबर है।
प्रश्न 3.
क्या ये त्रिभुज सर्वांगसम भी हैं ?
उत्तर:
हाँ, ये त्रिभुज सर्वांगसमता के SSS गुण के अनुसार सर्वांगसम है।
प्रश्न 4.
इनमें से प्रत्येक त्रिभुज का क्षेत्रफल कितना है ?
हल:
प्रत्येक त्रिभुज का क्षेत्रफल
= \(\frac { 1 }{ 2 } \) × आयत का क्षेत्रफल
= \(\frac { 1 }{ 2 } \) × (l × b) = \(\frac { 1 }{ 2 } \) × 8 × 5 = 20 cm2
इनमें से प्रत्येक त्रिभुज का क्षेत्रफल 20 cm2 है।
![]()
प्रश्न:
अब एक 5 cm भुजा वाला वर्ग लीजिए और इसे 4 त्रिभुजों में बाँटिए जैसा कि आकृति में दिखाया गया है (चित्र 11.7)।
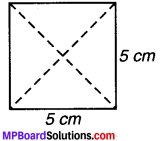
प्रश्न 1.
क्या चारों त्रिभुजों का क्षेत्रफल बराबर है ?
उत्तर:
हाँ, चारों त्रिभुजों का क्षेत्रफल बराबर है।
प्रश्न 2.
क्या वे एक-दूसरे के सर्वांगसम हैं ?
उत्तर:
हाँ, वे एक-दूसरे के सर्वांगसम हैं।
प्रश्न 3.
प्रत्येक त्रिभुज का क्षेत्रफल क्या है ?
हल:
प्रत्येक त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 4 } \) × वर्ग का क्षेत्रफल
= \(\frac { 1 }{ 4 } \) × 5 × 5
= \(\frac { 25 }{ 4 } \) = 6.25 cm2
पाठ्य-पुस्तक पृष्ठ संख्या # 226
![]()
इन्हें कीजिए
प्रश्न 1.
आगे दिए गए सभी आयत जिसकी लम्बाई 6.cm और चौड़ाई 4 cm है, सर्वांगसम बहुभुज से मिलकर बने हैं। प्रत्येक बहुभुज का क्षेत्रफल ज्ञात कीजिए।
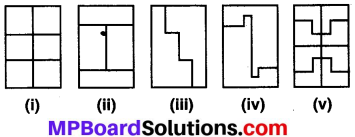
हल:
आयत की लम्बाई = 6 cm, चौड़ाई = 4 cm,
आयत सर्वांगसम बहुभुज बनाते हैं।
प्रत्येक दशा में बहुभुज का क्षेत्रफल
= आयत का क्षेत्रफल
= l × b = 6 × 4 = 24 cm2
(i) चूँकि आकृति में कुल छ: बहुभुज हैं।
∴ प्रत्येक बहुभुज का क्षेत्रफल = \(\frac { 24 }{ 6 } \) = 4 cm2
(ii) ∵ आकृति में कुल 4 बहुभुज हैं।
∴ प्रत्येक आकृति का क्षेत्रफल = \(\frac { 24 }{ 6 } \) = 6 cm2
(iii) ∵ आकृति में 2 बहुभुज हैं।
∴ प्रत्येक आकृति का क्षेत्रफल
= \(\frac { 24 }{ 2 } \) = 12 cm2
(iv) ∵ आकृति में कुल 2 बहुभुज हैं।
∴ प्रत्येक आकृति का क्षेत्रफल
= \(\frac { 24 }{ 2 } \) = 12 cm2
(v) ∵ आकृति में कुल 8 बहुभुज हैं।
∴ प्रत्येक आकृति का क्षेत्रफल
= \(\frac { 24 }{ 8 } \) = 3 cm2
पाठ्य-पुस्तक पृष्ठ संख्या # 227-228
पाठ्या-पुस्तक में दिये गये समान्तर चतुर्भुजों के बारे में सोचिए।
आकृतियों द्वारा घेरे गए वर्गों की संख्या को गिनकर समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए और भुजाओं को मापकर परिमाप भी ज्ञात कीजिए।
तालिका को पूरा कीजिए।
हल:
समान्तर चतुर्भुज की प्रत्येक आकृति में वर्गों की संख्या 15 है। इसलिए प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल
= 15 वर्ग इकाई
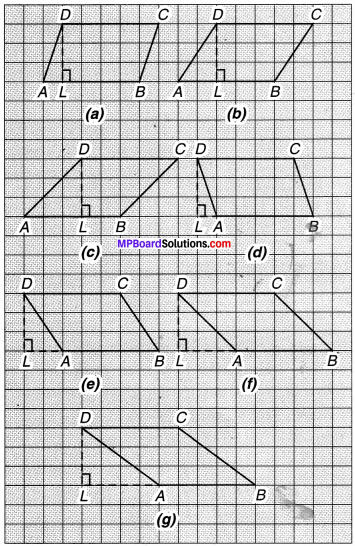
परिमाप निकालने के लिए प्रत्येक समान्तर चतुर्भुज की भुजा AD को नापते हैं।
आकृति : (a) AD = 3.2 इकाई,
∴ परिमाप = 2(l + b) = 2(5 + 3.2) = 16.4 इकाई
(b) AD = 3.6 इकाई,
∴ परिमाप = 2(5 + 3.6) = 17.2 इकाई
(c) AD = 4.2 इकाई,
∴ परिमाप = 2(5 + 4.2) = 18.4 इकाई
(d) AD = 3.2 इकाई,
∴ परिमाप = 2(5 + 3.2) = 16.4 इकाई
(e) AD = 3.6 इकाई,
∴ परिमाप = 2(5 + 3.6)
= 17.2 इकाई
(f) AD = 4.2 इकाई,
∴ परिमाप = 2(5 + 4.2) = 18.4 इकाई
(g) AD =5 इकाई,
∴ परिमाप = 2(5 + 5) = 20 इकाई
तालिका
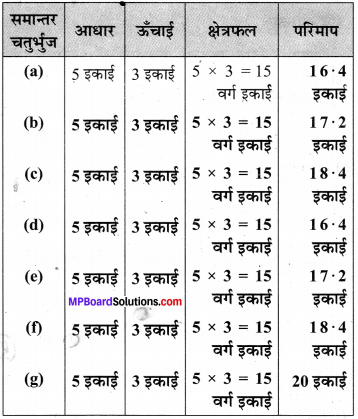
इकाई स्पष्ट है कि क्षेत्रफल सभी चतुर्भुजों का समान है, लेकिन परिमाप भिन्न हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 228
![]()
प्रश्न:
पाठ्य-पुस्तक में दिये गये 7 cm तथा 5 cm भुजाओं वाले समान्तर चतुर्भुजों को देखिए।
प्रत्येक समान्तर चतुर्भुज का परिमाप तथा क्षेत्रफल ज्ञात कीजिए। अपने परिणाम का विश्लेषण कीजिए।
हल:
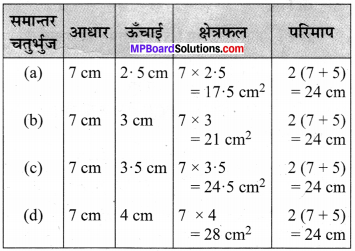
यहाँ, स्पष्ट है कि समान्तर चतुर्भुजों का क्षेत्रफल अलग-अलग है, लेकिन परिमाप समान हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 229
इन्हें कीजिए
प्रश्न 1.
निम्न समान्तर चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए:
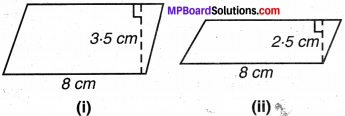
(iii) समान्तर चतुर्भुज ABCD में AB = 7.2 cm और C से AB पर लम्ब 4.5 cm है।
हल:
(i) आधार = 8 cm, ऊँचाई = 3.5 cm
∴ क्षेत्रफल = आधार × ऊँचाई
= 8 cm × 3.5 cm = 28 cm2
(ii) आधार = 8 cm, ऊँचाई = 2.5 cm
∴ क्षेत्रफल = आधार × ऊँचाई
=8 cm × 2.5 cm = 20 cm2
(iii) समान्तर चतुर्भुज का आधार AB = 7.2 cm
ऊँचाई = 4.5cm
क्षेत्रफल = आधार × ऊँचाई
= 7.2 cm × 4.5 cm
= 32.40 cm2
पाठ्य-पुस्तक पृष्ठ संख्या # 230
इन्हें कीजिए
प्रश्न 1.
ऊपर दिए गए क्रियाकलापों को अलग-अलग प्रकार के त्रिभुज लेकर कीजिए।
हल:
दिया है, ∆ABC हम दूसरा ∆ACD इस प्रकार लेते हैं कि समान्तर चतुर्भुज ABCD दिखाई दे, जैसा कि चित्र 11:11 में दिखाया गया है :
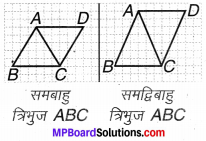
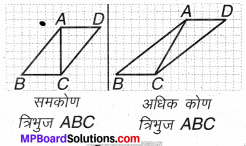
ऊपर की प्रत्येक आकृति में, ∆ABC के क्षेत्रफल का दो गुना समान्तर चतुर्भुज ABCD के क्षेत्रफल के बराबर है।
क्योंकि हम जानते हैं कि ∆ABC का क्षेत्रफल
= \(\frac { 1 }{ 2 } \) (आधार × ऊँचाई)
तथा समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई होता है।
प्रश्न 2.
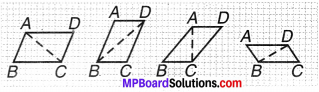
अलग-अलग प्रकार के समान्तर चतुर्भुज लीजिए। प्रत्येक समान्तर चतुर्भुज को दो त्रिभुजों में एक विकर्ण के अनुदिश काटिए। क्या ये त्रिभुज सर्वांगसम हैं ?
हल:
दिया है, ABCD एक समान्तर चतुर्भुज है। प्रत्येक चतुर्भुज दो त्रिभुजों में विकर्ण AC अथवा BD के अनुदिश काटा, जैसा कि चित्र 11.12 में दिखाया गया है। ये त्रिभुज आपस में सर्वांगसम होंगे।
प्रश्न 3.
चित्र 11.13 में सभी त्रिभुज, आधार AB = 6 cm पर स्थित हैं। आधार AB पर प्रत्येक त्रिभुज की संगत ऊँचाई के बारे में आप क्या कह सकते हैं ?
क्या हम कह सकते हैं कि सभी त्रिभुजों का क्षेत्रफल बराबर है?
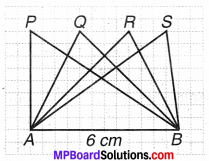
हल:
चित्र से स्पष्ट है कि प्रत्येक त्रिभुज की संगत ऊँचाई आधार AB पर बराबर है।
∵ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
अतः हम कह सकते हैं कि समान आधार और बराबर ऊँचाई के त्रिभुजों का क्षेत्रफल बराबर है।
प्रश्न 4.
आधार 6 cm वाले एक अधिक कोण त्रिभुज (obtuse angled triangle) त्रिभुज ABC पर विचार करते हैं।
इसकी ऊँचाई AD शीर्ष A से DC पर लम्ब है जो त्रिभुज के बाह्य स्थित है।
क्या आप इस त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं ?
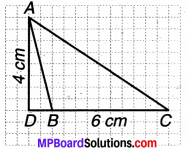
हल:
हाँ, इसका क्षेत्रफल ज्ञात कर सकते हैं।
∆ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
= \(\frac { 1 }{ 2 } \) × BC × AD
= \(\frac { 1 }{ 2 } \) × 6 × 4 = 12 cm2
पाठ्य-पुस्तक पृष्ठ संख्या # 232-234