MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.2
पाठ्य-पुस्तक पृष्ठ संख्या # 299
प्रश्न 1.
रूलर का प्रयोग करके 7.3 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद:
(1) कागज पर एक बिन्दु A लेते हैं।
(2) अब पैमाने को सीधा रखकर उसका शून्य A पर रखते हैं।

(3) पेंसिल की सहायता से A से 7.3 सेमी की दूरी पर बिन्दु B पर निशान लगाते हैं।
(4) A को B से मिलाते हैं। इस प्रकार प्राप्त रेखाखण्ड AB वांछित रेखाखण्ड है।
प्रश्न 2.
रूलर और परकार का प्रयोग करते हुए 5.6 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद :
(1) एक रेखा l खींचते हैं और इस पर एक बिन्दु P लेते हैं।

(2) परकार की नोंक को पैमाने के शून्य पर रखते हैं और परकार को इस प्रकार खोलते हैं कि पेंसिल पैमाने के 5.6 सेमी तक पहुँचे।
(3) परकार की नोंक को बिन्दु P पर रखते हैं।
(4) अब परकार में भरी दूरी से रेखा l पर एक चाप लगाते हैं, जो l को बिन्दु Q पर काटता है।
इस प्रकार रेखाखण्ड \(\overline { PQ } \) अभीष्ट रेखाखण्ड है।
![]()
प्रश्न 3.
7.8 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) खींचिए। इसमें से \(\overline { AC } \) काटिए जिसकी लम्बाई 4.7 सेमी हो। BC को मापिए।
हल :
रचना के पदः

(1) 7.8 सेमी लम्बाई का एक रेखाखण्ड AB खींचा।
(2) यहाँ, \(\overline { AB } \) = 7.8 सेमी और \(\overline { AC } \) = 4.7 सेमी
अब परकार की सहायता से इस रेखाखण्ड पर बिन्दु C इस प्रकार काटते हैं कि AC = 4.7 सेमी।
(3) \(\overline { BC } \) को मापने पर, \(\overline { BC } \) = 3.1 सेमी।
प्रश्न 4.
3.9 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) दिया हुआ है। एक रेखाखण्ड \(\overline { PQ } \) खींचिए जो रेखाखण्ड \(\overline { AB } \) का दो गुना हो। मापन से अपनी रचना की जाँच कीजिए।

(संकेत: \(\overline { PX } \) खींचिए ताकि \(\overline { PX } \) लम्बाई \(\overline { AB } \) की लम्बाई के बराबर हो। फिर \(\overline { XQ } \) काटिए ताकि \(\overline { XQ } \) की लम्बाई भी \(\overline { AB } \) की लम्बाई के बराबर हो। इस प्रकार \(\overline { PX } \) और \(\overline { XQ } \) की लम्बाई मिलकर \(\overline { AB } \) की लम्बाई का दो गुना हो जाएगी।)
हल :
रचना के पद :
(i) एक रेखा l खींचते हैं।
(ii) AB = 3.9 सेमी खींची।
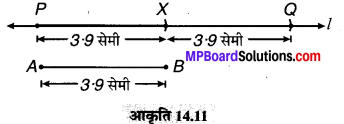
(iii) रेखा l में से \(\overline { PX } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
(iv) अब \(\overline { XQ } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
अत: \(\overline { AB } \) की दो गुनी लम्बाई के लिए \(\overline { PX } \) और \(\overline { XQ } \) लम्बाई जोड़ते हैं।
जाँच : \(\overline { AB } \) + \(\overline { AB } \) = 3.9 सेमी + 3.9 सेमी
2 \(\overline { AB } \) = 7.8 सेमी = \(\overline { PQ } \)
अत: \(\overline { AB } \) का दो गुना = \(\overline { PQ } \)
![]()
प्रश्न 5.
7.3 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) और 3.4 सेमी लम्बाई का रेखाखण्ड \(\overline { CD } \) दिया हुआ है। एक रेखाखण्ड \(\overline { XY } \) खींचिए ताकि \(\overline { XY } \) की लम्बाई \(\overline { AB } \) और \(\overline { CD } \) की लम्बाइयों के अन्तर के बराबर हो।
हल :
रचना के पद :
(1) सर्वप्रथम रेखाखण्ड \(\overline { AB } \) = 7.3 और \(\overline { CD } \) = 3.4 सेमी खींचते हैं।

(2) एक रेखा l खींचते हैं और इस पर कोई बिन्दु X लेते हैं।
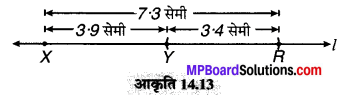
(3) अब \(\overline { XR } \) इस प्रकार लेते हैं कि \(\overline { XR } \) की लम्बाई = \(\overline { AB } \) की लम्बाई = 7.3 सेमी
(4) अब \(\overline { RY } \) = \(\overline { CD } \) की लम्बाई (3.4 सेमी) इस प्रकार काटते हैं कि
\(\overline { XY } \) की लम्बाई = \(\overline { AB } \) की लम्बाई – \(\overline { CD } \) की लम्बाई
जाँच : मापने पर, हम प्राप्त करते हैं
\(\overline { XY } \) = 3.9 सेमी = 7.3 सेमी – 3.4 सेमी
= \(\overline { AB } \) – \(\overline { CD } \)
अतः \(\overline { XY } \) = \(\overline { AB } \) – \(\overline { CD } \)