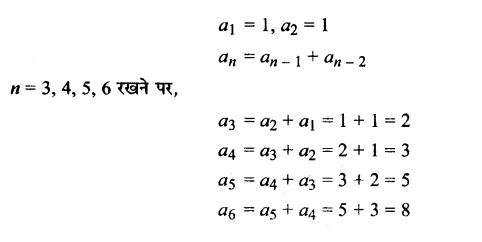MP Board Class 11th Maths Solutions Chapter 9 अनुक्रम तथा श्रेणी Ex 9.1
प्रश्न 1 से 6 तक के अनुक्रमों में प्रत्येक के प्रथम पाँच पद लिखिए, जिनका गवाँ पद दिया गया है :
प्रश्न 1.
an = n(n+ 2).
हल:
an = n(n + 2)
n का मान 1, 2, 3, 4, 5 रखने पर
a1 = 1 x 3 = 3, a2 = 2 x 4 = 8, a3 = 3 x 5 = 15, a4 = 4 x 6 = 24, a5 = 5 x 7 = 35
अतः दिए गए अनुक्रम के पाँच पद 3, 8, 15, 24, 35 हैं।
![]()
प्रश्न 2.
an = \(\frac{n}{n+1}\)
हल:
an = \(\frac{n}{n+1}\)
n का मान 1, 2, 3, 4, 5 रखने पर
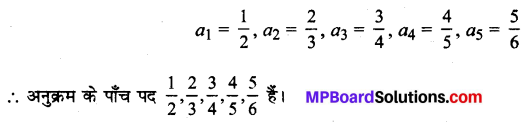
प्रश्न 3.
an = 2n.
हल:
an = 2n में n का मान 1, 2, 3, 4, 5 रखने पर
\(a_{1}=2^{1}=2, a_{2}=2^{2}=4, a_{3}=2^{3}=8, a_{4}=2^{4}=16, a_{5}=2^{5}=32\)
अतः अनुक्रम के पाँच पद 2, 4, 8, 16, 32 हैं।
प्रश्न 4.
an = \(\frac{2 n-3}{6}\)
हल:
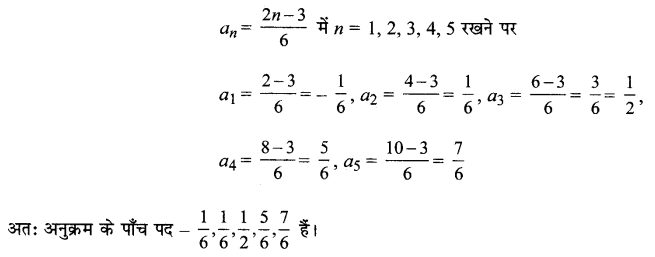
![]()
प्रश्न 5.
an = \((-1)^{n-1} 5^{n+1}\).
हल:
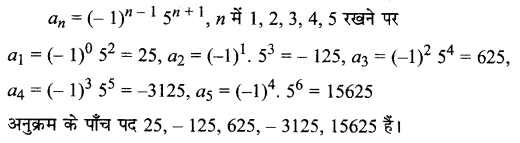
प्रश्न 6.
an = \(n \frac{n^{2}+5}{4}\)
हल:

निम्नलिखित प्रश्न 7 से 10 तक के अनुक्रमों में प्रत्येक का वांछित पद ज्ञात कीजिए, जिनका n वाँ पद दिया गया है:
प्रश्न 7.
an = 4n – 3, 417, a24.
हल:
an = 4n – 3
n = 17 लेने पर,
a17 = 4 x 17 – 3 = 68 – 3 = 65
n = 24 लेने पर,
a24 = 4 x 24 – 3 = 96 – 3 = 93.
![]()
प्रश्न 8.
\(a_{n}=\frac{n^{2}}{2^{n}}\) : a7
हल:
\(a_{n}=\frac{n^{2}}{2^{n}}\)
n= 7 रखने पर,
\(a_{7}=\frac{7^{2}}{2^{7}}=\frac{49}{128}\)
प्रश्न 9.
an = \((-1)^{n-1} n^{3}\); an.
हल:
an = \((-1)^{n-1} n^{3}\),
n = 9 रखने पर,
a9 = \((-1)^{9-1} 9^{3}\) = 729.
![]()
प्रश्न 10.
an = \(\frac{n(n-2)}{n+3}\) : a20.
हल:
an = \(\frac{n(n-2)}{n+3}\),
n = 20 लेने पर,
\(a_{20}=\frac{20 \times 18}{23}=\frac{360}{23}\)
प्रश्न 11 से 13 तक प्रत्येक अनुक्रम के पाँच पद लिखिए तथा संगत श्रेणी ज्ञात कीजिए:
प्रश्न 11.
\(a_{1}=3, a_{n}=3 a_{n-1}+2\) सभी n > 1 के लिए।
हल:

प्रश्न 12.
\(a_{1}=-1, a_{n}=\frac{a_{n-1}}{n}\), जहाँ n ≥ 2.
हल:

प्रश्न 13.
a1 = a2 = 2, \(a_{n}=a_{n-1}-1\), जहाँ n > 2.
हल:

प्रश्न 14.
Fibonacci अनुक्रम निम्नलिखित रूप में परिभाषित है :
\(1=a_{1}=a_{2}\), तथा \(a_{n}=a_{n-1}+a_{n-2}, n>2\) तो, \(\frac{a_{n+1}}{a_{n}}\) ज्ञात कीजिए जबकि n = 1, 2, 3, 4, 5.
हल :