MP Board Class 11th Maths Solutions Chapter 7 क्रमचय और संचयं Ex 7.4
प्रश्न 1.
यदि \(^{n} C_{8}=^{n} C_{2}\), तो nC2 ज्ञात कीजिए।
हल:

![]()
प्रश्न 2.
n का मान निकालिए, यदि
(i) \(^{2 n} C_{3}:^{n} C_{2}\) = 12 : 1
(ii) \(^{2 n} C_{3}:^{n} C_{2}\) = 11 : 1
हल :
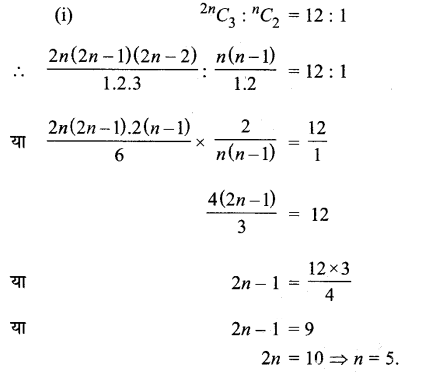

प्रश्न 3.
किसी वृत्त पर स्थित 21 बिन्दुओं से होकर जाने वाली कितनी जीवाएँ खींची जा सकती हैं?
हल:
21 बिन्दुओं में कोई 2 बिन्दु मिलाने से एक जीवा प्राप्त होती है।
जीवाओं की संख्या = \(^{21} C_{2}=\frac{21 \times 20}{1 \times 2}=210\).
प्रश्न 4.
5 लड़के और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमें बनाने के कितने तरीके हैं?
हल:
5 लड़कों में से 3 लड़कों के चुनने के तरीके = \(^{5} C_{3}\)
4 लड़कियों में से 3 लड़कियाँ चुनने के तरीके = \(^{4} C_{3}\)
∴ 5 लड़कों और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमों की संख्या
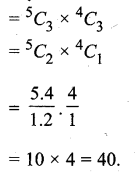
![]()
प्रश्न 5.
6 लाल रंग की, 5 सफेद रंग की और 5 नीले रंग की गेंदों में से 9 गेंदों के चुनने के तरीकों की संख्या कीजिए, यदि प्रत्येक संग्रह में प्रत्येक रंग की 3 गेंदें हैं।
हल:
6 लाल रंग की गेंदों में से 3 गेंदें चुनने के तरीके = \(^6 C_{3}\)
5 सफेद रंग की गेंदों में से 3 गेंदें चुनने के तरीके = \(^5 C_{3}\)
5 नीले रंग की गेंदों में से 3 गेंदें चुनने के तरीके = \(^5 C_{3}\)
इस प्रकार 6 लाल, 5 सफेद तथा 5 नीले रंग की गेंदों में से प्रत्येक रंग की 3 गेंदों के चुनने के तरीके.
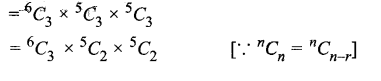
= \(\frac{6.5 .4}{1.2 .3} \times \frac{5.4}{1.2} \times \frac{5.4}{1.2}\)
= 20 x 10 x 10
= 2000.
प्रश्न 6.
52 पत्तों की एक गड्डी में से 5 पत्तों को लेकर बनने वाले संचयों की संख्या निर्धारित कीजिए, यदि प्रत्येक संचय में तथ्यतः एक इक्का हो।
हल:
ताश का गड्डी में 4 इक्के होते हैं।
∴ 4 में से 1 इक्का चुनने के तरीके = \(^{4} C_{1}\)
इक्का छोड़कर शेष पत्ते = 52 – 4 = 48
48 पत्तों में से कोई 4 अन्य पत्ते चुनने के तरीके = \(^{48} C_{4}\)
∴ ताश की गड्डी में 1 इक्का और 4 अन्य पत्ते चुनने के तरीके
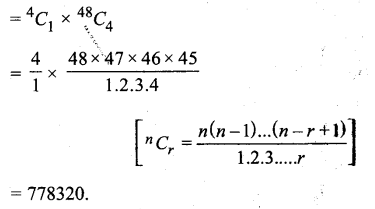
प्रश्न 7.
17 खिलाड़ियों में से, जिनमें केवल 5 गेंदबाजी कर सकते हैं, एक क्रिकेट टीम के 11 खिलाड़ियों का चयन कितने प्रकार से किया जा सकता है, यदि प्रत्येक टीम में तथ्यतः 4 गेंदबाज हैं?
हल:
5 गेंदबाज में 4 गेंदबाज चुनने के तरीके = \(^{5} C_{4}\)
शेष खिलाड़ी = 17 – 5 = 12
शेष चुने जाने वाले खिलाड़ी = 11 – 4 = 7
∴ 12 खिलाड़ियों में से 7 खिलाड़ी चुनने के तरीके = \(^{12} C_{7}\)
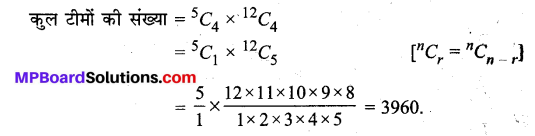
![]()
प्रश्न 8.
एक थैली में 5 काली तथा 6 लाल गेंदें हैं। 2 काली तथा 3 लाल गेंदों के चयन के तरीकों की संख्या निर्धारित कीजिए।
हल:
5 काली गेंदों में से 2 गेंदें चुनने के तरीके = \(^{5} C_{2}\)
6 लाल गेंदों में से 3 गेंदें चुनने के तरीके = \(^6 C_{3}\)
5 काली व 6 लाल गेंदों में से 2 काली और 3 लाल गेंदें चुनने के कुल तरीके
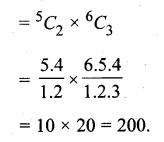
प्रश्न 9.
9 उपलब्ध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है, यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ट पाठ्यक्रम अनिवार्य हैं?
हल:
दो पाठ्यक्रम अनिवार्य हों, तब शेष पाठ्यक्रम = 9 – 2 = 7 .
7 पाठ्यक्रमों में से 3 पाठ्यक्रम चुनने के तरीके = \(^{7} \mathrm{C}_{3}\)
अत: 9 में से 5 पाठ्यक्रम चुनने के तरीके = \(^{7} C_{3}=\frac{7 \times 6 \times 5}{1 \times 2 \times 3}\) = 35