MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1

प्रश्न 1.
निम्नलिखित डिग्री माप के संगत रेडियन माप ज्ञात कीजिए:
(i) 25°
(ii) – 47° 30′
(iii) 240°
(iv) 520°
हल:
(i) 180° = π रेडियन

MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-2

प्रश्न 2.
निम्नलिखित रेडियन माप के संगत डिग्री माप ज्ञात कीजिए (π = \(\frac{22}{7}\)) का प्रयोग करें :
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-3
हल:

प्रश्न 3.
एक पहिया एक मिनट में 360° परिक्रमण करता है तो एक सेकंड में कितने रेडियन माप का कोण बनाएगा?
हल:
1 परिक्रमण में पहिया द्वारा बना कोण = 21 रेडियन
∴ 360 परिक्रमण में पहिया द्वारा बना कोण = 360 × 2π रेडियन
∵ 1 मिनट अर्थात् 60 सेकण्ड में 360 × 2π रेडियन का कोण बनता है।
∴ 1 सेकण्ड में पहिया द्वारा बना कोण = \(\frac{360 \times 2 \pi}{60}\)
= 12π रेडियन।

प्रश्न 4.
एक वृत्त जिसकी त्रिज्या 100 सेमी है, 22 सेमी लंबाई की चाप वृत्त के केन्द्र पर कितने डिग्री माप का कोण बनाएगी? (π = \(\frac{22}{7}\) का प्रयोग कीजिए)
हल:
∵ चाप = त्रिज्या × कोण
जहाँ चाप, l = 22 सेमी
त्रिज्या r = 100 सेमी
22 = 100 × θ
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-7

प्रश्न 5.
एक वृत्त जिसका व्यास 40 सेमी. है, की एक जीवा 20 सेमी. लंबाई की है तो इसके संगत छोटे चाप की लंबाई ज्ञात कीजिए।
हल:
व्यास = 40 सेमी
त्रिज्या = 20 सेमी
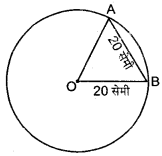
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-8
त्रिभुज OAB एक समबाहु त्रिभुज है
∠AOB = 60°
= \(\frac{60 \times \pi}{180}\) रेडियन
= \(\frac{\pi}{3}\) रेडियन
मान लीजिए चाप AB = l
केन्द्र O पर चाप द्वारा बना कोण, θ = \(\frac{\pi}{3}\)
चाप AB की लम्बाई,
l = rθ = 20 × \(\frac{\pi}{3}\) रेडियन
= \(\frac{20 \pi}{3}\) रेडियन।

प्रश्न 6.
यदि दो वृत्तों के समान लंबाई वाले चाप अपने केन्द्रों पर क्रमशः 60° तथा 75° के कोण बनाते हों, तो उनकी त्रिज्याओं का अनुपात ज्ञात कीजिए।
हल:
माना चाप की लंबाई = l
चाप द्वारा केन्द्र पर बना कोण θ₁ = 60°
= \(\frac{\pi}{3}\) रेडियन
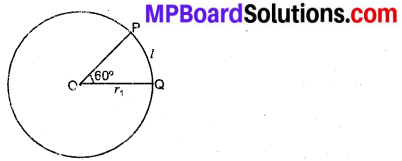
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-9
मान लीजिए इसकी त्रिज्या = r₁
l = r₁θ₁
= r₁ \(\frac{\pi}{3}\)
∴ r₁ = \(\frac{3 l}{\pi}\) …(i)
दूसरे वृत्त के लिए,
माना त्रिज्या = r₂
चाप की लंबाई = l
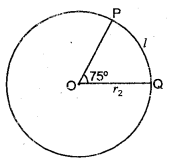
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-10
चाप द्वारा केन्द्र पर बना कोण, θ₂ = 75°

समीकरण (i) को समीकरण (ii) से विभाजित करने पर
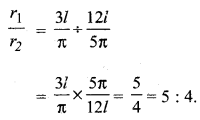
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-12

प्रश्न 7.
75 सेमी लम्बाई वाले एक दोलायमान दोलक का एक सिरे से दूसरे सिरे तक दोलन करने से जो कोण बनता है, उसका माप रेडियन में ज्ञात कीजिए, जबकि उसके नोक द्वारा बनाए गए चाप की लम्बाई निम्नलिखित हैं :
(i) 10 सेमी
(ii) 15 सेमी
(iii) 21 सेम
हल:
त्रिज्या = 75 सेमी
(i) चाप की लम्बाई l₁ = 10 सेमी
यदि चाप द्वारा केन्द्र पर बना कोण θ रेडियन हो, तो
l₁ – rθ₁
10 = 75θ₂
MP Board Class 11th Maths Solutions Chapter 3 त्रिकोणमितीय फलन Ex 3.1 img-13