MP Board Class 11th Maths Important Questions Chapter 4 Principle of Mathematical Induction

MP Board Class 11th Maths Important Questions Chapter 4 Principle of Mathematical Induction

Principle of Mathematical Induction Important Questions

Principle of Mathematical Induction Long Answer Type Questions

Question 1.
For n > 1, prove that with the help of principle of mathematical induction :
1² + 2² + 3² + 4² + …………. + n² = \(\frac { n(n + 1)(2n + 1) }{ 6 }\). (NCERT)
Solution:

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 2.
For n ≥ 1 prove that :
\(\frac { 1 }{ 1.2 }\) + \(\frac { 1 }{ 2.3 }\) + \(\frac { 1 }{ 3.4 }\) + …………. + \(\frac { 1 }{ n(n + 1) }\) = \(\frac { n }{ n + 1 }\)
Solution:
Let

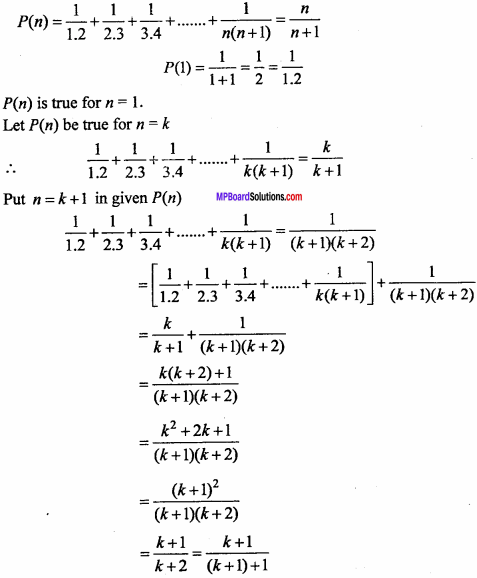
∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.
Instruction:
All questions from 3 to 7 when n∈N prove the statement by using principle of mathematical induction :

Question 3.
1³ + 2³ + 3³ + …………. + n³ = \(\frac { { n }^{ 2 }{ (n+1) }^{ 2 } }{ 4 }\) (NCERT)
Solution:

∴ Given function is true for n = m + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 4.
1 + \(\frac { 1 }{ 1 + 2 }\) + \(\frac { 1 }{ 1 + 2 + 3 }\) + ……….. + \(\frac { 1 }{ 1 + 2 + 3 + ………. + n }\) + …………. + = \(\frac { 2n }{ n + 1 }\).
Solution:
For n = 1, L.H.S = 1
and R.H.S. = \(\frac { 2 x 1 }{ 1 + 1 }\) = 1
The given function is true for n = 1.
Let the function be true for n = m

∴ The Given function is true for n = m + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 5.
1.2 + 2.3 + 3.4 + ………….. + n(n + 1) = \(\frac { n(n + 1)(n + 2) }{ 3 }\)
Solution:
Let p(n) = 1.2 + 2.3 + 3.4 + ………….. + n(n + 1) = \(\frac { n(n + 1)(n + 2) }{ 3 }\)
If n = 1, L.H.S. = 1.2 = 2
R.H.S = \(\frac { n(n + 1)(n + 2) }{ 3 }\) = \(\frac { 1.2.3 }{ 3 }\) = 2
∴ p(n) is true for n = 1.
Let p(n) be true for n = k

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 6.
\(\frac { 1 }{ 2.5}\) + \(\frac { 1 }{ 5.8 }\) + \(\frac { 1 }{ 8.11}\) + …………. + \(\frac { 1 }{ (3n – 1)(3n + 2) }\) = \(\frac { n }{ 6n + 4 }\)
Solution:
Let p(n) = \(\frac { 1 }{ 2.5}\) + \(\frac { 1 }{ 5.8 }\) + \(\frac { 1 }{ 8.11}\) + …………. + \(\frac { 1 }{ (3n – 1)(3n + 2) }\) = \(\frac { n }{ 6n + 4 }\)
∴ For n = 1, L.H.S = \(\frac { 1 }{ 2.5}\) = \(\frac { 1 }{ 10}\)
and R.H.S = \(\frac { 1 }{ 6.1 + 4}\) = \(\frac { 1 }{ 10}\)
∴ p(n) is true for n = 1.
Let p(n) be true for n = k

∴ p(n) is true for n = k + 1.
Hence, p(n) is true for all values of n ∈ N.

Question 7.
1.2.3. + 2.3.4 + …………. + n(n+1)(n+2) = \(\frac { n(n + 1)(n + 2)(n + 3) }{ 4 }\). (NCERT)
Solution:
For n = 1, L.H.S = 1.2.3 = 6
And R.H.S. = \(\frac { 1(1 + 1)(1 + 2)(1 + 3) }{ 4 }\) = \(\frac { 2.3.4 }{ 4 }\) = 6
∴ Given function is true for n = 1.
Let the function be true for n = k

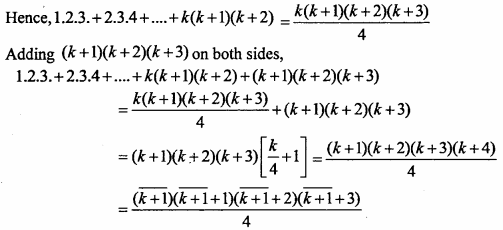
∴ The given function is true for n = k + 1. Hence the given function is true for all values of n ∈ N.

Question 8.
Prove that (41)ⁿ – (14)ⁿ is a multiple of 27 with the help of principle of mathematical induction. (NCERT)
Solution:
Let P(n) = (41)ⁿ – (14)ⁿ
For n = 1,
P(1) = (41)¹ – (14)¹= 27
Which is multiple of 27.
Let P(ri) be true for n = k.
Then, (41)^k – (14)^k = 27m
Put n = k +1 in P(n)
(41)^k+1 – (14)^k+1 = (41)^k.41 – (14)^k. 14
= (41)^k.41 – 41.(14)^k + 41.(14)^k – (14)^k.14
= 41[(41)^k – (14)^k]+(14)^k [41 – 14]
= 41 x 27m + (14)^k x 27 = 27[41 x m + (14)^k]
Which is multiple of 27.
If the given function P(n) is true for n = k then P(n) will be true for U n = k +1 also.
Hence the given function is true for all values of n ∈ N.

MP Board Class 11th Maths Important Questions