MP Board Class 11th Maths Important Questions Chapter 3 Trigonometric Functions
Trigonometric Functions Important Questions
Trigonometric Functions Objective Type Questions
(A) Choose the correct option :
Question 1.
The value of 1 + cosθ is :
(a) 2sin2 θ
(b) \(\frac { { sin }^{ 2 }\theta }{ 2 }\)
(c) 2cos2 θ
(d) cos2 θ
Answer:
(c) 2cos2 θ
Question 2.
The value of \(\frac { cos 11° + sin 11° }{ cos 11° – sin 11° }\) is :
(a) cot 56°
(b) cot 34°
(c) tan 34°
(d) tan 56°
Answer:
(d) tan 56°
Question 3.
The value of sin 18° is :
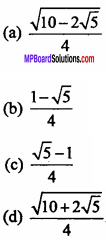
Answer:
![]()
Question 4.
The value of cos 1° cos 2° cos 3° ………… cos 179° is :
(a) 0
(b) 1
(c) – 1
(d) None of these
Answer:
(a) 0
Question 5.
The value of \(\frac { 3 π }{ 2 }\) radian in degree.
(a) 120°
(b) 170°
(c) 220°
(d) 270°
Answer:
(d) 270°
Question 6.
The value of cos2 (60 + α) + cos2 (60 – α) + cos2 α = ……………
(a) 3
(b) \(\frac { 3 π }{ 2 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 3 }{ 4 }\)
Answer:
(b) \(\frac { 3 π }{ 2 }\)
Question 7.
Amplitude of the function f(x) = 2 sin x is :
(a) π
(b) 2π
(c) 1
(d) 2
Answer:
(d) 2
Question 8.
Period of the function f(x) = tan x is :
(a) π
(b) 2
(c) \(\frac { π }{ 2 }\)
(d) – π
Answer:
(a) π
Question 9.
Solution of the equation 4 sin2θ = 1 is :
(a) nπ ± \(\frac { π }{ 3 }\), n ∈ I
(b) 2nπ ± \(\frac { π }{ 3 }\), n ∈ I
(c) nπ ± \(\frac { π }{ 6 }\), n ∈ I
(d) 2nπ ± \(\frac { π }{ 6 }\), n ∈ I
Answer:
(c) nπ ± \(\frac { π }{ 6 }\), n ∈ I
Question 10.
Maximum value of 3cosθ + 4sinθ is :
(a) 3
(b) 4
(c) 5
(d) 7
Answer:
(c) 5
Question 11.
If tanθ = – \(\frac { 4 }{ 3 }\) , then the value of sinθ is :
(a) – \(\frac { 4 }{ 5 }\) but not \(\frac { 4 }{ 5 }\)
(b) \(\frac { 4 }{ 5 }\) but not \(\frac – { 4 }{ 5 }\)
(c) – \(\frac { 4 }{ 5 }\) or \(\frac { 4 }{ 5 }\)
(d) None of these
Answer:
(c) – \(\frac { 4 }{ 5 }\) or \(\frac { 4 }{ 5 }\)
Question 12.
The value of tan15° + cot15° is :
(a) 1
(b) 3
(c) 2
(d) 4
Answer:
(d) 4
Question 13.
The value of sin50° + sin70° + sin10° is :
(a) 0
(b) 1
(c) – 1
(d) None of these
Answer:
(a) 0
Question 14.
One value of θ which satisfy the equation cosθ +\/3sinθ = 2 is :
(a) \(\frac { π }{ 2 }\)
(b) \(\frac { π }{ 3 }\)
(c) \(\frac { 2π }{ 3 }\)
(d) \(\frac { π }{ 4 }\)
Answer:
(b) \(\frac { π }{ 3 }\)
Question 15.
The general value of θ satisfying the equation cosθ = , tanθ = 1is :
(a) 2nπ + \(\frac { 5π }{ 4 }\)
(b) 2nπ – \(\frac { 5π }{ 4 }\)
(c) 2nπ + \(\frac { π }{ 4 }\)
(d) 2nπ – \(\frac { π }{ 4 }\)
Answer:
(a) 2nπ + \(\frac { 5π }{ 4 }\)
(B) Match the following :

Answer:
- (d)
- (c)
- (a)
- (b)
- (g)
- (j)
- (e)
- (i)
- (h)
- (f)
(C) Fill in the blanks :
- The value of cos 18° = ……………….
- The value of sin 75° = ……………….
- If tan A = \(\frac { 5 }{ 6 }\) and tan B = \(\frac { 1 }{ 3}\), then the value of A + B = ……………….
- 2π radian is equal to ………………. right angle.
- If sinθ + cosθ = 1, then the value of sinθ.cosθ = ……………….
- The value of \(\frac { 3tanA-{ tan }^{ 3 }A }{ 1-3{ tan }^{ 2 }A }\) = ……………….
- Solution of the equation cos2θ = cos2θ is ……………….
- Amplitude of 3cosx is ……………….
- The value of cot 22\(\frac { 1 }{ 2 }\)° is ……………….
- If tan θ tan 2θ = 1, then the value of θ is ……………….
- The value of sin(A + B).sin(A – B) = ……………….
- The length of the arc of a circle of radian 6 cm substending an angle of 30° at the centre of the circle is ……………….
Answer:
- \(\frac { \sqrt { 10+2\sqrt { 5 } } }{ 4 }\)
- \(\frac { \sqrt { 3 } + 1 }{ 2\sqrt { 2 } }\)
- 45°
- 4
- 0
- tan 3A
- nπ
- 3
- \(\sqrt {2}\) + 1
- (n + \(\frac { 1 }{ 3}\))\(\frac { π }{ 3 }\)
- sin2A – sin2B
- πcm
(D) Write true / false :
- The value of tan 105° is \(\frac { \sqrt { 3 } + 1 }{ 2\sqrt { 2 } }\)
- The value of sin 3A is 4 sin3 A + 3sinA
- The value of cos2 A – sin2B is cos(A + B) cos (A – B)
- The value of cos2 48°- sin2 12 is \(\frac { \sqrt { 5 } + 1 }{ 4 }\).
- The value of cos2 (\(\frac { π }{ 6 }\) + θ) + sin2 (\(\frac { π }{ 6 }\) – θ) is 0.
- If x is a real, then the equation sinθ = x + \(\frac { 1 }{ x }\) has unique solution.
- Solution of tan2 θ + cot2 θ = 2 is 2nπ + \(\frac { π }{ 6 }\)
- If f(x) = sin2 x, then f(- x) = sin2 x
- The value of sin\(\frac { 5π }{ 12 }\).cos\(\frac { π }{ 12 }\) is \(\frac { \sqrt { 3 } – 2 }{ 4 }\).
- If A + B = \(\frac { π }{ 3 }\) and cosA + cosB = 1, then cos(A – B) = – \(\frac { 1 }{ 3 }\).
Answer:
- False
- False
- True
- True
- False
- False
- False
- True
- False
- True
(E) Write answer in one word / sentence :
- Find the solution of equation cos2 θ – sin2 θ – \(\frac { 1 }{ 4 }\) = 0
- The value of tan 1° tan 2° tan 3° ……………. tan 18° is :
- The value of sin(A + B) + sin(A – B) is :
- If (1 + tan x) (1 + tan y) = 2, then find the value of (x + y):
- The value of sin( \(\frac { π }{ 3 }\) + x) – sin(\(\frac { π }{ 4 }\) – x)
Answer:
- θ = nπ + (-1)n\(\frac { π }{ 6 }\)
- 1
- 2sinA.cosB
- \(\frac { π }{ 4 }\)
- \(\sqrt { 2 }\) sinx
Trigonometric Functions Short Answer Type Questions
Question 1.
A wheel makes 360 revolutions in 1 min. then how many radians measure of an angle does it turn in 1 second? (NCERT)
Solution:
In 60 seconds number of revolutions of wheel = 360
∴ In 1 second number of revolutions of wheel = \(\frac { 360 }{ 60 }\)
∴ In one revolution angle made = 360° = 2π
∴ In 6 revolutions angle made = 2π x 6 = 12π radian
Question 2.
Find the degree measure of an angle substended at the centre of a circle of radius 100 cm by an arc of length 22 cm.
Solution:
We know that, θ = \(\frac { 1 }{ r }\), length of arc = l = 22 cm, radius = r = 100 cm, angle made at the centre = θ = ?
Applying formula θ = \(\frac { 1 }{ r }\)
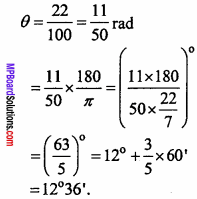
Question 3.
In a circle of diameter 40 cm, the length of chord is 20 cm, then find the length of minor arc of the chord.
Solution:
Radius of circle = OA = OB = \(\frac { 40 }{ 2 }\) = 20 cm, AB = 20 cm
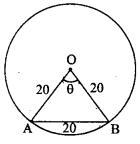
Hence OAB is an equilateral triangle.
∴ θ = \(\frac { 1 }{ r }\)
⇒ 60° = \(\frac { AB }{ 20 }\)
⇒ AB = 60° x 20 = 60 x \(\frac { π }{ 180 }\) x 20
= \(\frac { 20π }{ 3 }\) cm.
Question 4.
If in two circles, arc of the same length substend angles of 60° and 75° at the centre, then find the ratio of their radii. (NCERT)
Solution:
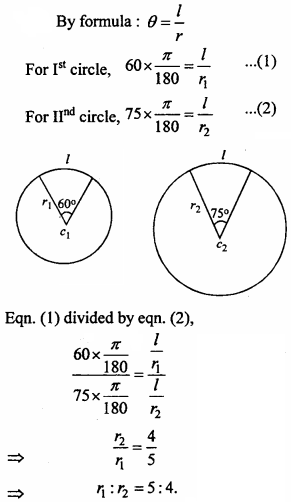
Question 5.
Find value : (i) sin75°, (ii) tan15°
Solution:

Question 6.
Prove that:
sin2\(\frac { π }{ 4 }\) + cos2\(\frac { π }{ 3 }\) = – \(\frac { 1 }{ 2 }\)
Solution:
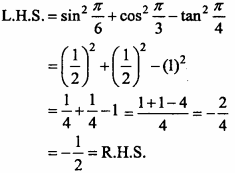
Question 7.
Prove that:
cos 27°. tan 27°. tan 63°. cosec 63° = 1. (NCERT)
Solution:
L.H.S. = cos 27°. tan 27°.tan 63°. cosec 63°
= cos 27°. tan 27° tan(90° – 27°). cosec (90° – 27°)
= cos 27°. tan 27° cot 27°. sec 27°
= \(\frac { 1 }{ sec 27° }\).\(\frac { 1 }{ cot 27° }\)cot 27°. sec 27° sec 27° cot 27°
= 1 = R.H.S.
Question 8.
Find the general solution of the following equations :
- sinθ = \(\frac { \sqrt { 3 } }{ 2 }\)
- tanθ = 1
- \(\sqrt { 3 }\) tanθ + 1 = 0.
Solution:
1. sinθ = \(\frac { \sqrt { 3 } }{ 2 }\)
⇒ sinθ = sin\(\frac { π }{ 3 }\)
∴ θ = nπ + ( – 1)n\(\frac { π }{ 3 }\) [ ∵ sinθ = sinα ⇒ θ = nπ + (- 1)nα, where n ∈ I]
2. tanθ = 1
⇒ tanθ = tan\(\frac { π }{ 4 }\)
∴ θ = nπ + \(\frac { π }{ 4 }\) [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]
3. \(\sqrt { 3 }\) tanθ + 1 = 0.
⇒ tanθ = – \(\frac { 1 }{ \sqrt { 3 } }\) = – tan\(\frac { π }{ 6 }\)
⇒ tanθ = tan (π – \(\frac { π }{ 6 }\))
⇒ tanθ = tan\(\frac { 5π }{ 6 }\)
∴ θ = nπ + \(\frac { 5π }{ 4 }\) [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]
Question 9.
Solve the following equations :
(i) 4 sin2 θ = 1
(ii) 3 tan2 θ = 1.
Solution:
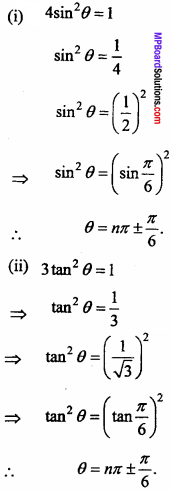
Question 10.
Find the principal value of x :
tan x = \(\sqrt { 3 }\)
Solution:
tan x =\(\sqrt { 3 }\)
tan x = tan\(\frac { π }{ 3 }\) = tan(π + \(\frac { π }{ 3}\))
⇒ tan x = tan\(\frac { π }{ 3 }\) = tan\(\frac { 4π }{ 3 }\)
⇒ x = \(\frac { π }{ 3 }\) or \(\frac { 4π }{ 3 }\)
Principal value of x = \(\frac { π }{ 3 }\)
∴ tan x = \(\sqrt { 3 }\) ⇒ tanx = tan\(\frac { π }{ 3 }\)
Hence, general solution of x = nπ + \(\frac { π }{ 3 }\), [ ∵tanθ = tanα ⇒ θ = nπ + α, where n ∈ I]
Question 11.
Find the principal value of x :
sec x = 2.
Solution:
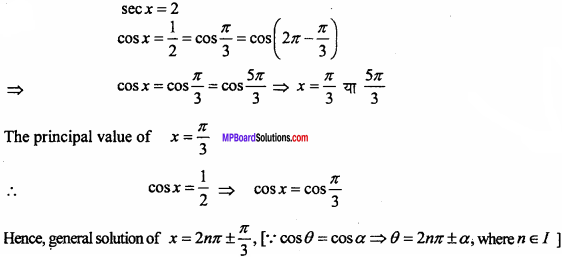
Trigonometric Functions Long Answer Type Questions
Question 1.
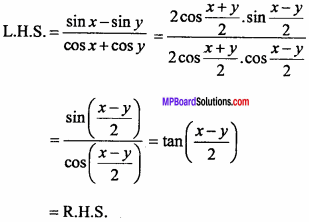
Prove that:
\(\frac { sinx – siny }{ cosx + cosy }\) = tan\(\frac { x – y }{ 2 }\)
Solution:
Question 2.
Prove that:
\(\frac { sin3x + sinx }{ cos3x + cosx }\) = tan2x.
Solution:
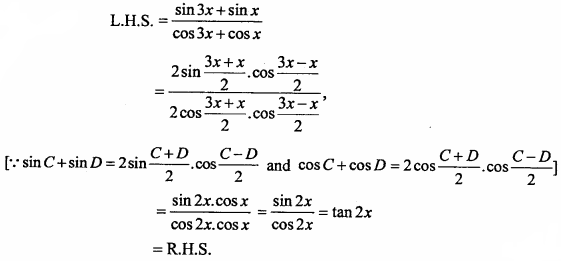
Question 3.
Prove that:
\(\frac { sinx – sin3x }{ { sin }^{ 2 }x – { cos }^{ 2 }x }\) = 2 sinx.
Solution:
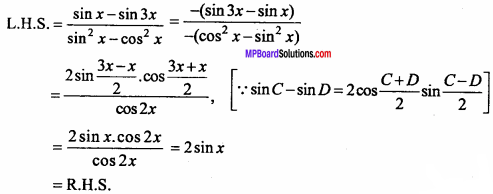
Question 4.
Prove that:
\(\frac { cos9x – cos5x }{ sin17x – sin3x }\) = – \(\frac { sin2x}{ cos10x }\)
Solution:
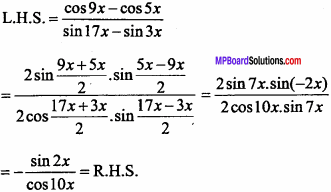
Question 5.
Prove that:
\(\frac { sin5x + sin3x }{ cos5x + cos3x }\) = tan4x.
Solution:
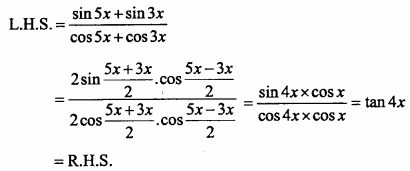
Question 6.
Prove that:
2sin2\(\frac { π }{ 6 }\) + cosec2\(\frac { 7π }{ 6 }\)cos2\(\frac { π }{ 3 }\) = \(\frac { 3 }{ 2 }\)
Solution:
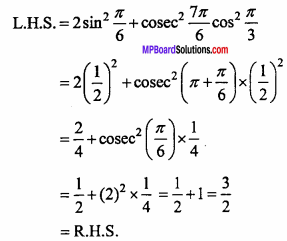
Question 7.
Prove that:
cot2\(\frac { π }{ 6 }\) + cosec\(\frac { 5π }{ 6 }\) + 3tan2\(\frac { π }{ 6 }\) = 6
Solution:
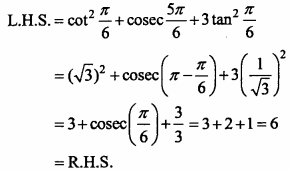
Question 8.
Prove that:
2sin2\(\frac { 3π }{ 4 }\) + 2cos2\(\frac { π }{ 4 }\) + 2sec2\(\frac { π }{ 3 }\) = 10
Solution:
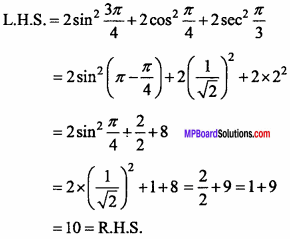
Question 9.
Prove that:
\(\frac { cos11° + sin11° }{ cos11° – sin11° }\) = tan56°
Solution:
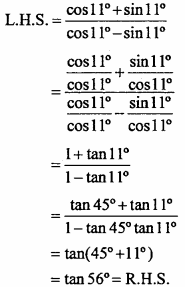
Question 10.
Prove that:
tan 3A – tan 2A – tan A = tan 3A. tan 2A. tan A.
Solution:
tan3A – tan2A – tanA – tan3A.tan2A. tanA = 0
⇒ tan3A – tan2A – tanA (l + tan3A.tan2A) = 0
⇒ tan 3A – tan 2A = tan A (1 + tan 3 A. tan 2 A)
⇒ \(\frac { tan 3A – tan 2A}{ 1 + tan 2A.tan 3A }\)
⇒ tan(3A – 2 A) = tan A
⇒ tanA = tan A.
Question 11.
Prove that:
cos(\(\frac { π }{ 4 }\) + x) + cos(\(\frac { π }{ 4 }\) – x) = \(\sqrt {2}\)cosx
Solution:

Question 12.
Prove that:
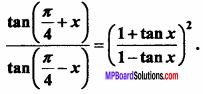
Solution:
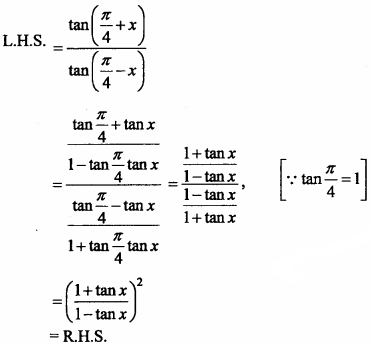
Question 13.
If α + β = \(\frac { π }{ 4 }\), then prove that :
(1 + tanα)(1 + tanβ) = 2.
Solution:
Given α + β = \(\frac { π }{ 4 }\)
tan(α + β) = tan \(\frac { π }{ 4 }\)
![]()
⇒ tan α + tan β = 1 – tanα.tan β
⇒ tan α + tan β.tanα.tan β = 1
⇒ tan α + tan β(1 + tanα) = 1
⇒ 1 + tan α + tan β(1 + tanα) = 1 + 1
⇒ ( 1 + tan α)(1 + tan β) = 2
Question 14.
Find the general solution of cos4x = cos 2x.
Solution:
Given equation :
cos4x = cos2x
⇒ cos4x – cos2x = 0
⇒ – 2sin\(\frac { 4x + 2x}{ 2 }\).sin\(\frac { 4x – 2x}{ 2 }\) = 0
⇒ – 2sin3x.sinx = 0
⇒ sinx.sin3x = 0
⇒ sin3x = 0 or sinx = 0
⇒ 3x = nπ or x = nπ
⇒ x = \(\frac { nπ}{ 3 }\) or x = nπ, where n∈I.
Question 15.
Solve the equation tan 2x = cot(x + \(\frac { π }{ 3 }\))
Solution:
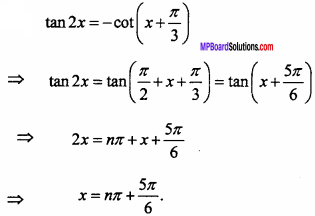
Question 16.
Solve the equation sin 3θ = sin 2θ
Solution:
Given equation sin3θ = sin2θ
sin 3θ – sin 2θ = 0
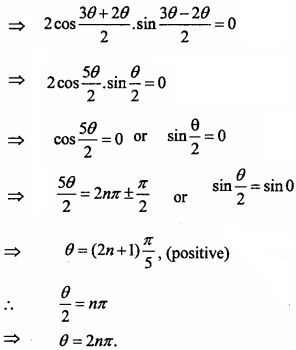
Question 17.
Solve the equation tan2θ = tan\(\frac { 2 }{ θ }\)
Solution:
tan 2θ = tan\(\frac { 2 }{ θ }\)
⇒ 2θ = nπ + \(\frac { 2 }{ θ }\)
⇒ 2θ – \(\frac { 2 }{ θ }\) = nπ + \(\frac { 2 }{ θ }\)
⇒ 2θ – \(\frac { 2 }{ θ }\) = nπ
⇒ 2θ2 – 2 = nπθ
⇒ 2θ2 – nπθ – 2 = 0
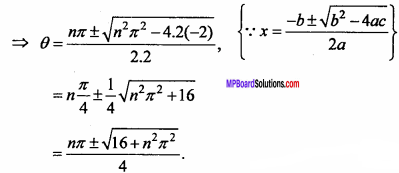
Question 18.
Solve the equation tanθ.tan2θ = 1
Solution:
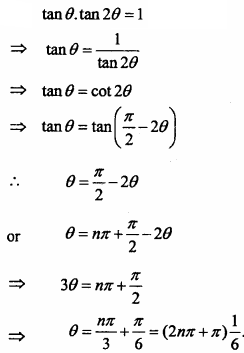
Question 19.
If sec x = \(\frac { 13 }{ 5 }\) and x is in fourth quadrant, then find the other five trigonometrical functions (NCERT)
Solution:
secx = \(\frac { 13 }{ 5 }\) ,
Given : x is in fourth quadrant,
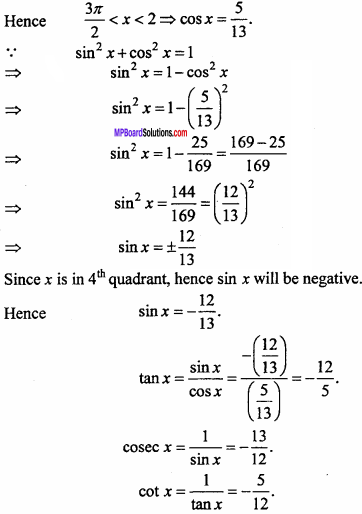
Question 20.
If tan x = – \(\frac { 5 }{ 12 }\) and x is in second quadrant, then find the other five trigonometrical functions (NCERT)
Solution:
Given : tan x = – \(\frac { 5 }{ 12 }\) ,
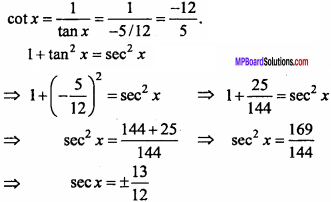
∴ x is in second quadrant, ∵ secx is negative.
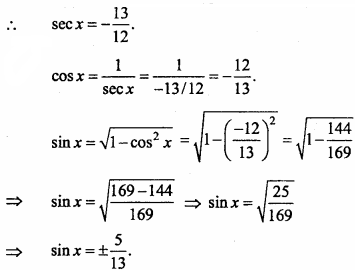
∵ x is in second quadrant, hence sinx is positive.
sinx = \(\frac { 5 }{ 13 }\)
cosecx = \(\frac { 1 }{ sin x }\) = \(\frac { 1 }{ 5/13 }\) = \(\frac { 13 }{ 5 }\)
Question 21.
Prove that:
cos 20°. cos 40°. cos 60°. cos 80°= \(\frac { 1 }{ 16 }\) .
Solution:
L.H.S. = cos 20° .cos 40°. cos 60°. cos 80°
= cos 20°.cos 40°.\(\frac { 1 }{ 2 }\). cos80°
= \(\frac { 1 }{ 4 }\)(2 cos 20°. cos 40°). cos 80°
= \(\frac { 1 }{ 4 }\)(cos 60° + cos 20°). cos 80°
= \(\frac { 1 }{ 4 }\) cos 60°. cos 80° + \(\frac { 1 }{ 4 }\) cos 20°. cos 80°
= \(\frac { 1 }{ 4 }\). \(\frac { 1 }{ 2}\). cos 80° + \(\frac { 1 }{ 8 }\)(2 cos 20°. cos 80°)
= \(\frac { 1 }{ 8 }\)cos 80° + \(\frac { 1 }{ 8 }\) (cos 100° + cos 60°)
= \(\frac { 1 }{ 8 }\)cos 80°+\(\frac { 1 }{ 8 }\)[cos(180° – 80°) + \(\frac { 1 }{ 2 }\)
= \(\frac { 1 }{ 8 }\)cos80° + \(\frac { 1 }{ 8 }\)(- cos80°) + \(\frac { 1 }{ 16 }\) [∵cos(180° – θ]= – cosθ]
= \(\frac { 1 }{ 8 }\)cos 80° – \(\frac { 1 }{ 8 }\)cos 80°+ \(\frac { 1 }{ 16 }\)
= \(\frac { 1 }{ 16 }\) = R.H.S.
Question 22.
Prove that:
sin 20°.sin40°.sin60°.sin80°=\(\frac { 3 }{ 16 }\).
Solution:

Question 23.
prove that:
(cosx + cosy)2+ (sinx – siny)2 = 4cos2\(\frac { x + y }{ 2 }\)
Solution:
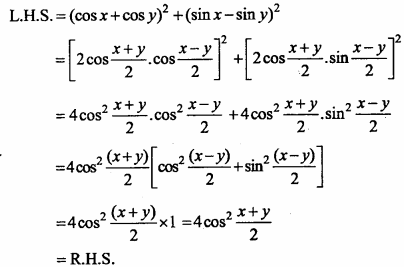
Question 24.
prove that:
(cosx – cosy)2+ (sinx – siny)2 = 4sin2\(\frac { x – y }{ 2 }\)
Solution:
L.H.S. = (cosx – cosy)2+ (sinx – siny)2
= cos2x + cos2y – 2 cosxcosy + sin2x + sin2y – 2sinx siny
= cos2x + sin2x + cos2y + sin2y – 2[cosx cosy + sinx siny]
= 1 + 1 – 2cos(x – y) = 2 – 2cos(x – y)
= 2[1 – cos(x – y)] = 2 x 2sin2
= 4 sin2\(\frac { x – y }{ 2 }\) = R.H.S.
Question 25.
Prove that:
sinx + sin3x + sin5x + sin7x = 4 cosx cos2x sin4x.
Solution:
L.H.S. = sinx + sin3x + sin5x + sin 7x
= sin7x + sinx + sin5x + sin3x
= 2sin\(\frac { 7x + x }{ 2 }\).cos\(\frac { 7x – x }{ 2 }\) + 2sin\(\frac { 5x + 3x }{ 2 }\).cos\(\frac { 5x – 3x }{ 2 }\)
= 2sin4x.cos3x + 2sin4x.cosx
= 2sin4x[cos3x + cosx]
= 2sin4x[ 2 x cos\(\frac { 3x + x }{ 2 }\).cos\(\frac { 3x – x }{ 2 }\) ]
= 2sin4x[2cos2x.cosx]
= 4sin4x.cos2x.cosx
= R.H.S
Question 26.
Prove that:
![]()
Solution:

Question 27.
Solve the equation and find general solution of sec22x = 1 – tan2x. (NCERT)
Solution:
The given equation is :
sec2 2x = 1 – tan 2x
⇒ 1 + tan22x = 1 – tan 2x
⇒ tan2 2x = – tan2x
⇒ tan2 2x + tan2x = 0 ⇒ tan2x (tan2x + 1) = 0
⇒ tan2x = 0 tan2x(tan2x + 1) = 0 ⇒ 2x = nπ or tan2x = – 1
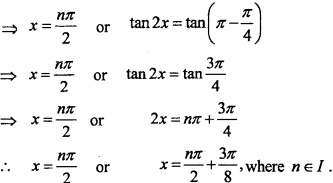
Question 28.
Solve the equation 2 cos2 x + 3 sin x = 0
Solution:
2 cos2 x + 3 sin x = 0
⇒ 2 (1 – sin2 x)+3 sinx = 0
⇒ 2 – 2sin2 x+ 3 sinx = 0
⇒ 2 sin2 x – 3 sinx – 2 = 0
⇒ 2 sin2 x + sinx – 4sinx – 2 = 0
⇒ sinx(2 sinx + 1) – 2(2sinx + 1) = 0
⇒ (2sinx + 1)(sinx – 2) = 0
⇒ 2 sin x +1 = 0 or sinx – 2 = 0
⇒ 2 sin x = – 1 = 0 or sinx = 2
⇒ 2 sin x = – \(\frac { 1 }{ 2 }\)
⇒ sin x = sin(π + \(\frac { π }{ 6 }\)
⇒ sin x = sin\(\frac { 7π }{ 6 }\)
∴ x = nπ + (- 1)n\(\frac { 7π }{ 6 }\)
Question 29.
Solve the equation tan2 θ + (1 – \(\sqrt { 3 }\)) tanθ = \(\sqrt { 3 }\)
Solution:
tan2 θ + (1 – \(\sqrt { 3 }\)) tanθ = \(\sqrt { 3 }\)
⇒ tan2 θ + (1 – \(\sqrt { 3 }\)) tanθ – \(\sqrt { 3 }\) = 0
⇒ tan2 θ + tanθ – \(\sqrt { 3 }\) tanθ – \(\sqrt { 3 }\) = 0
⇒ tanθ(tanθ + 1) – \(\sqrt { 3 }\)(tanθ + 1) = 0
⇒ (tanθ + 1)(tan θ – \(\sqrt { 3 }\)) = 0
⇒ tanθ + 1 = 0 or tan θ – \(\sqrt { 3 }\) = 0
⇒ tanθ = – 1 or tan θ = \(\sqrt { 3 }\)
⇒ tanθ = tan \(\frac { – π }{ 4 }\) = tanθ = tan\(\sqrt { 3 }\)
⇒ tanθ = tan \(\frac { – π }{ 4 }\) = θ = nπ + \(\frac { π }{ 3 }\)
∴ θ = nπ – \(\frac { π }{ 4}\)
Question 30.
Solve the equation \(\sqrt { 2 }\) secθ + tanθ = 1.
Solution:
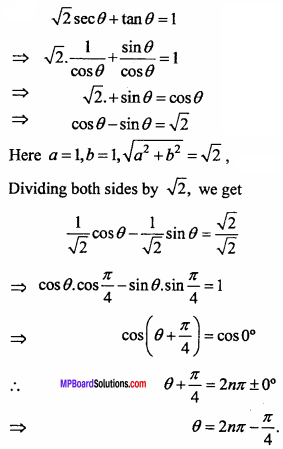
Question 31.
Find the general solution of the equation sinx + sin5x + sin5x = 0
Solution:
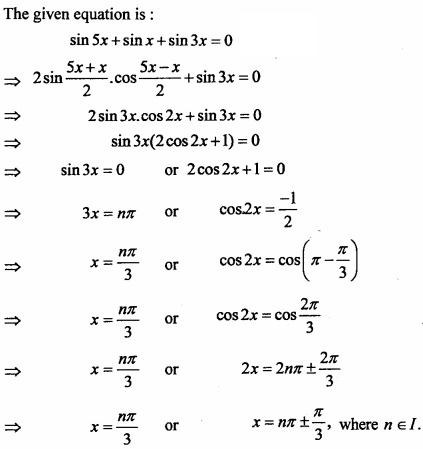
Question 32.
Prove that:
2cos\(\frac { π }{ 13 }\)cos\(\frac { 9π }{ 13 }\) + cos\(\frac { 3π }{ 13 }\) + cos\(\frac { 5π }{ 3 }\) = 0
Solution:

Question 33.
Prove that:
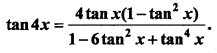
Solution:
