MP Board Class 11th Maths Important Questions Chapter 10 Straight Lines
Straight Lines Long Answer Type Questions
Question 1.
The slope of a line is double the slope of another line. If tangent of the angle between them is \(\frac {1}{3}\), then find the slope of the line.
Solution:
Let the angle between two lines be θ.
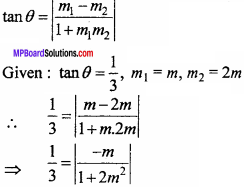
⇒ 1 + 2m2 = 3m
⇒ 2m2 – 3m + 1 = 0
⇒ 2m2 – 2m – m + 1 = 0
⇒ 2m(m – 1) – 1 (m – 1) = 0
⇒ (m – 1)(2m – 1) = 0
⇒ m = 1,\(\frac {1}{2}\)
Question 2.
If three points (h, 0), (a, b) and (0, k) lies on same line, then prove that \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1. (NCERT)
Solution:
Given points are A(h, 0), B(a, b) and C(0, k).

ab = (b – k)(a – h)
⇒ ab = ab – bh – ak + hk
⇒ bh + ak = hk
⇒ \(\frac {bh}{hk}\) \(\frac {ak}{hk}\) \(\frac {hk}{hk}\), (dividing both sides by hk)
⇒ \(\frac {a}{h}\) + \(\frac {b}{k}\) = 1.
Question 3.
Find the equation of the line passing through (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6). (NCERT)
Solution:
Gradient of AB = m = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
Where x1 = 2 , y1 = 5, x2 = – 3, y2 = 6
∴ m = \(\frac {6 – 5}{- 3 – 2}\) = \(\frac {1}{- 5}\)
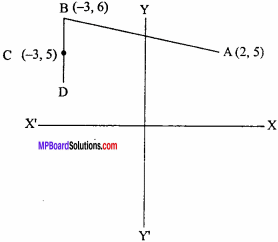
Let the gradient of CD = m1,
AB ⊥ CD
m x m1 = – 1
⇒ \(\frac {-1}{5}\) x m1 = – 1
⇒ m1 = 5
Equation of line CD will be :
y – y1 = m(x – x1)
Here x1 = – 3, y1 = 5, m = 5 .
⇒ y – 5 = 5(x + 3)
⇒ y – 5 = 5x + 15
⇒ 5x – y + 20 = 0.
![]()
Question 4.
Find the equation of straight line passing through the point (2, 2) and cutting off intercepts the axes whose sum is 9. (NCERT)
Solution:
Let the required equation of line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Given: a + b = 9 …. (2)
Line (1) passes through point (2, 2).
∴ \(\frac {2}{a}\) + \(\frac {2}{b}\) = 1
\(\frac {2a + 2b}{ab}\) = 1
2a + 2b = ab
Put b = 9 – a from equation (2), we get
2a + 2(9 – a) = a(9 – a)
⇒ 2a + 18 – 2a = 9a – a2
⇒ a2 – 9a + 18 = 0
⇒ a2 – 6a – 3a + 18 = 0
⇒ a (a – 6) – 3(a – 6) = 0
⇒ (a – 3)(a – 6) = 0
∴ a = 3 or a = 6
When a = 3, then b = 9 – a = 9 – 3 = 6
Hence the required equation is :
\(\frac {x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 2x + y = 6.
When a = 6, then b = 9 – 6 = 3
Hence the required equation is :
\(\frac {x}{6}\) + \(\frac {y}{3}\) = 1
⇒ x + 2 y = 6.
Question 5.
Find the equation to that straight line which passes through the point (7,9) and such that the portion between the axes is divided by the point in the ratio 3 : 1.
Solution:
Let the required equation of the line is :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 …. (1)
Let the required line cuts the axes at points A (a, 0) and B(0, b),
and Point P intercept the line AB internally in ratio 3 : 1.
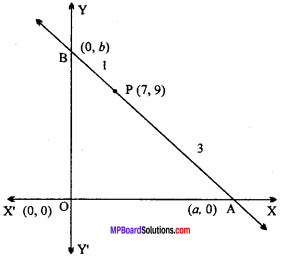
Putting values of a and b in eqn. (1), we get
\(\frac {x}{28}\) + \(\frac {y}{12}\) = 1
\(\frac {3x + 7y}{84}\) = 1
Hence required equation is 3x + 7y = 84.
Question 6.
Find the equation of the line which passes through the point (1, 2) and makes a right angled triangle with axes of area \(\frac {9}{2}\) sq units.
Solution:
Area of (∆AOB) = \(\frac {1}{2}\)a.b
⇒ \(\frac {9}{2}\) = \(\frac {1}{2}\)a.b
⇒ ab = 9
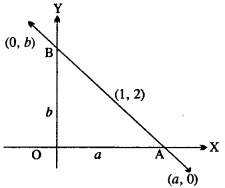
Let the equation of line \(\frac {x}{a}\) + \(\frac {y}{b}\) = 1 which passes through point (1, 2)
∴ \(\frac {1}{a}\) + \(\frac {2}{b}\) = 1
From equation (1), b = \(\frac {9}{a}\)
∴ \(\frac {1}{a}\) + \(\frac {2}{9}\) = 1
⇒ 9 + 2a2 = 9a
⇒ 2a2 – 9a + 9 = 0
⇒ 2a2 – 3a – 6a + 9 = 0
⇒ a(2a – 3) – 3(2.a – 3) = 0
⇒ (2a – 3)(a – 3) = 0
∴ b = 6, 3
Equation of line \(\frac {x}{3/2}\) + \(\frac {y}{6}\) = 1
⇒ \(\frac {2x}{3}\) + \(\frac {y}{6}\) = 1
⇒ 12x + 3y = 18
⇒ 4x + y = 6
or \(\frac {x}{3}\) + \(\frac {y}{3}\) = 1
⇒ x + y = 3
Question 7.
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then prove that \(\frac { 1 }{ { p }^{ 2 } }\) = \(\frac { 1 }{ { a }^{ 2 } }\) + \(\frac { 1 }{ { b }^{ 2 } }\) (NCERT)
Solution:
Equation of given line be :
\(\frac {x}{a}\) + \(\frac {y}{b}\) = 1
⇒ bx + ay = ab
⇒ bx + ay – ab = 0 …. (1)
Let the form of required equation be :
xcosα + ysinβ – p = 0 …. (2)
Comparing equation (1) and (2),

Question 8.
Find the angle between the lines.
y = (2 – \(\sqrt {3}\))x + 6 and y = (2 + \(\sqrt {3}\))x – 8.
Solution:
y = (2 – \(\sqrt {3}\))x + 6 … (1)
m1 = 2 – \(\sqrt {3}\)
Second line y = (2 + \(\sqrt {3}\))x – 8
m2 = 2 + \(\sqrt {3}\)
Let θ be the angle between them,
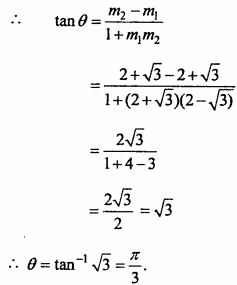
Question 9.
If the perpendicular drawn from origin on line y = mx + c intersect the line at point (- 1, 2), then find the value of m and c. (NCERT)
Solution:
Let the equation of AB be :
y = mx + c … (1)
Gradient of eqn. (1) is m and OP is perpendicular to AB
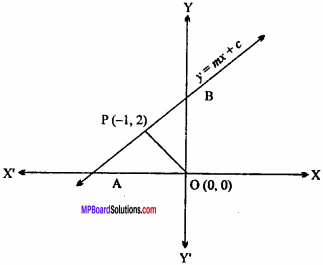
Gradient of OP m1 = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m1 = \(\frac {2 – 0}{- 1 – 0}\) = – 2
∵ Op ⊥ AB
∴ m × m1 = – 1
⇒ m(- 2) = – 1
⇒ m = \(\frac {1}{2}\)
put value of m in equation (1),
y = \(\frac {1}{2}\)x + c
Above equation passes through point (-1, 2), hence it will satisfy it.
2 = \(\frac {- 1}{2}\) + c
⇒ c = 2 + \(\frac {1}{2}\) = \(\frac {5}{2}\)
∴ m = \(\frac {1}{2}\), c = \(\frac {5}{2}\)
Question 10.
Find the coordinate of the foot of perpendicular from the point (- 1, 3) to the line 3x – 4y – 16 = 0.
Solution:
Equation of line CD is :
3x – 4y – 16 = 0 … (1)
Equation of line AB is perpendicular to equation (1),
4x + 3y + c = 0 … (2)
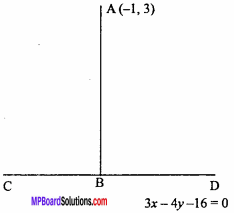
Equation (2) passes through point (- 1, 3).
∴ 4(- 1) + 3 x 3 + c = 0
– 4 + 9 + c = 0
c = – 5
Put c = – 5 in equation (2), we get 4x + 3y – 5 = 0
Now the intersection of lines (1) and (3) is the foot of perpendicular B
3x – 4y – 16 = 0
4x + 3y – 5 = 0
By cross multiplication method,

Question 11.
Find the equation of line parallel to y – axis and drawn through the point of intersection of line x – 7y + 5 = 0 and 3x + y = 0. (NCERT)
Solution:
Equation of given lines are :
x – 7y + 5 = 0 … (1)
3x + y = 0 … (2)
Equation of straight line passing through the intersection of equation (1) and (2) is :
x – 7y + 5 + λ(3x + y) = 0 … (3)

Put A = 7 in equation (3), we get
x – 7y + 5 + 7(3x + y) = 0
⇒ x – 7y + 5 + 21x + 7y = 0
⇒ 22x + 5 = 0.
Question 12.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point. (NCERT)
Solution:
Equation of given lines are :
3x + y – 2 = 0 … (1)
px + 2y – 3 = 0 … (2)
2x – y – 3 = 0 … (3)
From eqns. (1) and (3),
3x + y – 2 = 0
2x – y – 3 = 0
Solving by cross multiplication method,
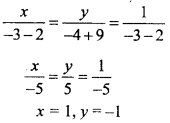
Lines intersect at the one point, hence point (1, – 1) will satisfy equation (2). p(1) – 2 x 1 – 3 = 0
p = 5.
Question 13.
Find the equation of a line drawn perpendicular to the line \(\frac {x}{4}\) + \(\frac {y}{6}\) = 1 through the point where it meets the y – axis. (NCERT)
Solution:
Given equation is :
\(\frac {x}{4}\) + \(\frac {y}{6}\) = 1
Line (1) meets the F – axis at point (0, 6).
From eqn. (1), \(\frac {6x + 4y}{24}\) = 1
⇒ 6x + 4y = 24
⇒ 6x + 4y – 24 = 0 … (2)
Equation of line perpendicular to eqn. (2),
4x – 6y + c = 0 … (3)
Above equation passes through point (0, 6).
∴ 4 x 0 – 6 x 6 + c = 0
c = 36
Put value of c = 36 in equation (3),
4x – 6y + 36 = 0
2x – 3y + 18 = 0.
![]()
Question 14.
For what value of k the equation (k – 3) x (4 – k2)y + k2 – 7k + 6 = 0 is :
- Parallel to X – axis
- Parallel to y – axis
- Passes through origin.
Solution:
Equation of given line is :
(k – 3)x – (4 – k2)y + k2 – 7k+6 = 0
(4 – k2)y = (k – 3)x + k2 – 7k + 6
⇒ y = \(\frac { (k – 3)x }{ 4 – { k }^{ 2 } }\) + \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)
1. Line parallel to X – axis :
∴ m = 0
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ k – 3 = 0
⇒ k = 3.
2. Line parallel to Y – axis :
∴ m = \(\frac {1}{0}\)
⇒ \(\frac { k – 3 }{ 4 – { k }^{ 2 } }\)
⇒ 4 – k2 = 0
⇒ k2= 4
⇒ k = ± 2
3. Line passing through origin, if c = 0.
∴ \(\frac { { k }^{ 2 } – 7k + 6 }{ 4 – { k }^{ 2 } }\)
⇒ k2 – 7k+6 = 0
⇒ k2 – 6k – k+6 = 0
⇒ k(k – 6) – 1(k – 6) = 0
⇒ (k – 6)(k – 6) = 0
∴ k = 1, 6
Question 15.
The line passing through the points (h, 3) and (4,1) meets the line 7x – 9y – 19 = 0 at right angle. Find the value of h.
Solution:
Equation of given line is :
7x – 9y – 19 = 0
⇒ 9y = 7x – 19
⇒ y = \(\frac {7}{9}\)x – \(\frac {19}{9}\) … (1)
Gradient of eqn. (1) m1 = \(\frac {7}{9}\)
Equation of line passing through points (h, 3) and (4, 1),
m2 = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)
m2 = \(\frac {1 – 3}{4 – h}\) = \(\frac {- 2}{4 – h}\)
∵ Lines are perpendicular.
∴m1 x m2= – 1
\(\frac {7(- 2)}{9(4 – h)}\) = – 1
⇒ – 14 = – 36 + 9h
⇒ 9h = 36 – 14
⇒ 9h = 22
∴ h =\(\frac {22}{9}\).
Question 16.
If the lengths of the perpendiculars drawn from origin on the straight lines xcosθ – y sinθ = kcos2θ and xsecθ + y cosec θ = k are p and q then prove that:
p2 + 4q2 = k2
Solution:
Equation of given lines :
xsecθ + ycosecθ = k … (1)
and x cosθ – y sinθ = k cos2θ … (2)
Length of perpendicular from origin on equation (1),

Adding equation (3) and (4),
4q2 + p2 = k2 sin2 2θ +k2 cos2 2θ
= k2(sin2 20 + cos22θ)
⇒ p2 + 4q2 = k2 .
Question 17.
Find the equation to the straight line passing through the intersection of lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 and makes an equal intercept on both the axes.
Solution:
Equation of given lines are :
4x + 7y – 3 = 0 … (1)
2x – 3y + 1 = 0 … (2)
Equation of straight line passing through intersection of lines (1) and (2),
4x + 7y – 3 + λ(2x – 3y + 1) = 0 … (3)
⇒ x(4 + 2 λ) + y(7 – 3 λ) – 3 + λ = 0
⇒ x(4 + 2 λ) + y(7 – 3 λ) = 3 – λ
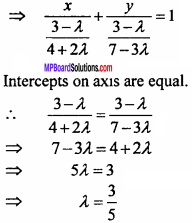
Put λ = \(\frac {3}{5}\) in equation (3),
4x + 7y – 3 + \(\frac {3}{5}\)(2x – 3y + 1) = 0
⇒ 20x + 35y – 15 + 6x – 9y +3 = 0
⇒ 26x + 26y = 12
⇒ 13x + 13y = 6.
⇒ 13x + 13y – 6 = 0.
Question 18.
Find the distance of point (-1, 1) from the line 12 (x + 6) = 5 (y – 2). (NCERT)
Solution:
Equation of given line is :
12(x + 6) = 5(y – 2)
⇒ 12x + 72 = 5y – 10
⇒ 12x – 5y + 82 = 0
Length of perpendicular

Question 19.
Find the points on the X – axis, whose distance from the line \(\frac {x}{3}\) + \(\frac {y}{4}\) = 1 are 4 units. (NCERT)
Solution:
Equation of given line is :
\(\frac {x}{3}\) + \(\frac {y}{4}\) = 1
⇒ 4x + 3y = 12
⇒ 4x + 3y – 12 = 0
Let the point on X – axis is (h, 0).
Length of perpendicular drawn from point (h, 0) is 4.

Taking (+) sign,
4h = 20 + 12 = 32
⇒ h = 8
Taking (-) sign,
4h = – 20 + 12
⇒ 4h = – 8
⇒ h = – 2
Point on X – axis are ( – 2, 0) and (8, 0).
![]()
Question 20.
Find the distance between two parallel lines : 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
Solution:
Equation of given lines are :
15x + 8y – 34 = 0
15x + 8y + 31 = 0
Put x = 0 in eqn. (1),
15(0) + 8y – 34 = 0
⇒ 8y = 34
y = \(\frac {34}{8}\) = \(\frac {17}{4}\)
Point (0, \(\frac {17}{4}\)) is on line (1),
Length of perpendicular from point (0, \(\frac {17}{4}\)) on equation (2),
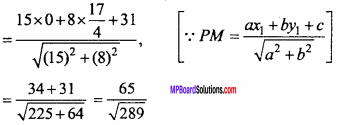
= \(\frac {65}{17}\) units
Hence the distance between lines is \(\frac {65}{17}\) units
Question 21.
The length L (in centimeters) of a copper rod is a linear function of its Celsius temperature C. In an experiment. If L = 124.942 when C= 20 and L = 125.134 when C = 110. Express L in terms of C. (NCERT)
Solution:
Given : L = 124.942 when C = 20
L = 125.134 when C= 110
In coordinate form points (20, 124.942) and (110, 125.134) are two points.
Required equation of straight line :
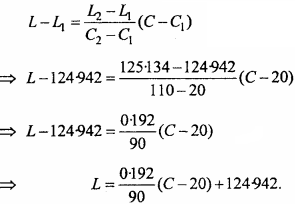
Question 22.
The owner of a milk store finds that he can sell 980 L of milk each week at Rs. 14/L and 1220 L of milk each week at Rs. 16/L. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17 L? (NCERT)
Solution:
Let price and litre be denoted in ordered pair (x, y), two points are (14, 980) and (16,1220).
∴ Required equation of straight line will be :
y – y1 = \(\frac { { y }_{ 2 } – { y }_{ 1 } }{ { x }_{ 2 } – { x }_{ 1 } }\)(x – x1)
⇒ y – 980 = \(\frac {1220 – 980}{16 – 14}\)(x – 14)
⇒ y – 980 = \(\frac {240}{2}\)(x – 14)
⇒ y – 980 = 120 (x – 14)
⇒ y – 980 = 120 x – 120 x 14
⇒ y = 120 x – 1680 + 980
⇒ y = 120 x – 700
When x = 17, then
y = 120 x 17 – 700
⇒ y = 2040 – 700
⇒ y = 1340
Hence, he will sell weekly 1340 L milk at the rate of Rs. 17 L.