MP Board Class 12th Physics Solutions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्
किरण प्रकाशिकी एवं प्रकाशिक यंत्र NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर
प्रश्न 1.
2.5 सेमी साइज़ की कोई छोटी मोमबत्ती 36 सेमी वक्रता त्रिज्या के किसी अवतल दर्पण से 27 सेमी दूरी पर रखी है। दर्पण से किसी परदे को कितनी दूरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिम्ब परदे पर बने। प्रतिबिम्ब की प्रकृति और साइज का वर्णन कीजिए। यदि मोमबत्ती को दर्पण की ओर ले जाएँ, तो परदे को किस ओर हटाना पड़ेगा?
हल :
दिया है, मोमबत्ती का साइज़ h = 2.5 सेमी, वक्रता त्रिज्या R = 36 सेमी, u = – 27 सेमी, दर्पण से पर की दूरी v = ?
अवतल दर्पण की फोकस दूरी \(f=-\frac{R}{2}=-\frac{36}{2}=-18\) सेमी
∴ दर्पण के सूत्र \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) से,
⇒ \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}=-\frac{1}{18}+\frac{1}{27}=\frac{-3+2}{54}=\frac{-1}{54}\)
या v= – 54 सेमी
अतः परदे को वस्तु की ही ओर दर्पण से 54 सेमी की दूरी पर रखना चाहिए।
पूनः \(m=\frac{h^{\prime}}{h}=\frac{-v}{u}\) से,
\(h^{\prime}=-\frac{v}{u} \times h ⇒h^{\prime}=-\frac{(-54)}{(-27)} \times 2.5=-5.0\) सेमी
प्रतिबिम्ब वास्तविक, आवर्धित तथा उल्टा बनेगा जिसकी लम्बाई 5.0 सेमी होगी।
∵ आंकिक रूप में u> f; अतः जैसे-जैसे मोमबत्ती को दर्पण की ओर ले जाएँगे वैसे-वैसे प्रतिबिम्ब का आकार बढ़ता जाएगा और उसकी दर्पण से दूरी भी बढ़ती जाएगी (जब तक कि u > f है); अत: परदे को धीरे-धीरे दर्पण से दूर हटाना होगा। जब u = f हो जाएगा तो प्रतिबिम्ब अनन्त पर बनेगा। इसके बाद u < f होने पर प्रतिबिम्ब आभासी तथा दर्पण के पीछे बनेगा। इस प्रतिबिम्ब को परदे पर प्राप्त नहीं किया जा सकता है
![]()
प्रश्न 2.
4.5 सेमी साइज़ की कोई सुई 15 सेमी फोकस दूरी के किसी उत्तल दर्पण से 12 सेमी दूर रखी है। प्रतिबिम्ब की स्थिति तथा आवर्धन लिखिए। क्या होता है जब सुई को दर्पण से दूर ले जाते हैं? वर्णन कीजिए।
हल :
सुई की लम्बाई h = 4.5 सेमी, उत्तल दर्पण हेतु f = + 15 सेमी, u = – 12 सेमी, v = ?, m = ?
दर्पण के सूत्र \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) से,
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{1}{15}+\frac{1}{12}=\frac{4+5}{60}=\frac{9}{60}\) या \(v=\frac{60}{9}=\frac{20}{3}\)= सेमी
अतः प्रतिबिम्ब, दर्पण से \(\frac{20}{3}\) सेमी दूरी पर दर्पण के पीछे बनता है।
किरण प्रकाशिकी एवं प्रकाशिक यन्त्र |481
∴ sinr = \(\frac{1 / \sqrt{2}}{1.14}\) = 0.62
∴ अपवर्तन कोण r = sin-1(0.62) = 38°
आवर्धन m = \(-\frac{v}{u}=\frac{-20 / 3}{-12}=+\frac{5}{9}\) तथा \(\frac{h^{\prime}}{h}=m\)
h’ = mh = \(\frac{5}{9}\) × 4.5 = 2.5 सेमी
प्रतिबिम्ब सीधा तथा 2.5 सेमी लम्बाई का है। जैसे-जैसे सुई को दर्पण से दूर ले जाते हैं (u → ∞) वैसे-वैसे प्रतिबिम्ब दर्पण के फोकस की ओर अग्रसर होता है।
प्रश्न 3.
कोई टैंक 12.5 सेमी ऊँचाई तक जल से भरा है। किसी सूक्ष्मदर्शी द्वारा बीकर की तली पर पड़ी किसी सुई की आभासी गहराई 9.4 सेमी मापी जाती है। जल का अपवर्तनांक क्या है? बीकर में उसी ऊँचाई तक जल के स्थान पर किसी 1.63 अपवर्तनांक के अन्य द्रव से प्रतिस्थापन करने पर सुई को पुनः फोकसित करने के लिए सूक्ष्मदर्शी को कितना ऊपर/नीचे ले जाना होगा?
हल :
पहली दशा में, सुई की वास्तविक गहराई h = 12.5 सेमी, आभासी गहराई h’ = 9.4 सेमी
∴ जल का वायु के सापेक्ष अपवर्तनांक \(a n_{w}=\frac{h}{h^{\prime}}=\frac{12.5}{9.4}\)
7 वाय के सापेक्ष अपवर्तनाक zassdf
⇒ anw = 1.33
दूसरी दशा में, द्रव का अपवर्तनांक anl
यदि इस दशा में आभासी गहराई h” है तो \(anl = \frac{h}{h^{\prime \prime}}\)
⇒ \(1.63=\frac{12.5}{h^{\prime \prime}}\)
⇒ \(h^{\prime \prime}=\frac{12.5}{1.63}=7.7\) सेमी
अब, h’- h” = 9.4 – 7.7 = 1.7 सेमी
अतः सूक्ष्मदर्शी को पुनः फोकसित करने के लिए, पूर्व दशा से 1.7 सेमी ऊपर उठाना होगा।
प्रश्न 4.
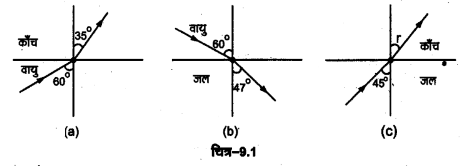
चित्र 9.1 (a) तथा (b) में किसी आपतित किरण का अपवर्तन दर्शाया गया है जो वायु में क्रमश: काँच-वायु तथा जल-वायु अन्तरापृष्ठ के अभिलम्ब से 60° का कोण बनाती है। उस आपतित किरण का अपवर्तन ‘कोण ज्ञात कीजिए, जो जल में जल-काँच अन्तरापृष्ठ के अभिलम्ब से 45° का कोण बनाती है [चित्र 9.1(c)]।
हल :
चित्र 9.1 (a) से, वायु से काँच में अपवर्तन हेतु i = 60°, r = 35°
∴ \(a n_{g}=\frac{\sin 60^{\circ}}{\sin 35^{\circ}}=\frac{0.866}{0.574}=1.51\)
चित्र 9.1 (b) से, वायु से जल में अपवर्तन हेतु i = 60, r= 47°
∴ \(a n_{w}=\frac{\sin 60^{\circ}}{\sin 47^{\circ}}=\frac{0.866}{0.656}=1.32\)
चित्र 9.1 (c) से, जल से काँच में अपवर्तन हेतु i = 45°, r = ?
\(w n_{g}=\frac{\sin 45^{\circ}}{\sin r} ⇒ \sin \dot{r}=\frac{\sin 45^{\circ}}{w^{n} g}\)
∵ \(\frac{1.51}{1.32}=1.14=w^{n} g=\frac{a^{n} g}{a^{n} w}\)
प्रश्न 5.
जल से भरे 80 सेमी गहराई के किसी टैंक की तली पर कोई छोटा बल्ब रखा गया है। जल के पृष्ठ का वह क्षेत्र ज्ञात कीजिए जिससे बल्ब का प्रकाश निर्गत हो सकता है। जल का अपवर्तनांक 1.33 है। (बल्ब को बिन्दु प्रकाश स्रोत मानिए)
हल :
माना जल से वायु में अपवर्तन हेतु क्रान्तिक कोण ic है।
स्पष्ट है कि बल्ब की केवल वही किरणें जल के पृष्ठ से अपवर्तित हो पाएँगी जिनके लिए जल-वायु पृष्ठ पर आपतन कोण ic अथवा उससे कम है। ये किरणें अर्द्धशीर्ष कोण ic का एक शंकु बनाएँगी। इस शंकु का जल-वायु अन्तरापृष्ठ द्वारा काटा गया अनुप्रस्थ परिच्छेद ही अभीष्ट प्रकाशित क्षेत्र होगा जो कि वृत्तीय आकार का होगा।
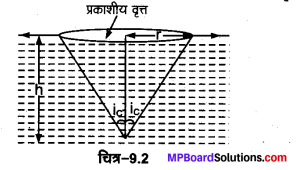
माना वृत्तीय पृष्ठ की त्रिज्या r है, तब tan ic = \(\frac{r}{h}\) ⇒ r=h tan ic
जबकि \(w n_{a}=\frac{1}{\sin i_{c}}\)
![]()
∴ वृत्त की त्रिज्या r= h tan ic = 0.80 × 1.13 = 0.904 मीटर [∵ tan 48.6° = 1.13]
∴ पृष्ठीय क्षेत्र = πr2 = 3.14 × (0.904)2 = 2.566 ≈ 2.6 मीटर2।
![]()
प्रश्न 6.
कोई प्रिज्म अज्ञात अपवर्तनांक के काँच का बना है। कोई समान्तर प्रकाश पुंज इस प्रिज्म के किसी फलक पर आपतित होता है। प्रिज्म का न्यूनतम विचलन कोण 40° मापा गया। प्रिज्म के पदार्थ का अपवर्तनांक क्या है? प्रिज्म का अपवर्तन कोण 60° है। यदि प्रिज्म को जल (अपवर्तनांक 1.33) में रख दिया जाए तो प्रकाश के समान्तर पुंज के लिए नए न्यूनतम विचलन कोण का परिकलन कीजिए।
हल :
दिया है, प्रिज्म के लिए A = 60°, वायु में δm = 40°

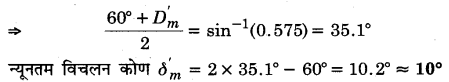
प्रश्न 7.
अपवर्तनांक 1.55 के काँच से दोनों फलकों की समान वक्रता त्रिज्या के उभयोत्तल लेन्स निर्मित करने हैं। यदि 20 सेमी फोकस दूरी के लेन्स निर्मित करने हैं तो अपेक्षित वक्रता त्रिज्या क्या होगी?
हल :
दिया है, n = 1.55, लेन्स की. फोकस दूरी f= + 20 सेमी .
माना अभीष्ट वक्रता त्रिज्या = R
तब उत्तल लेन्स हेतु R1 = + R, R2 = – R .
∴ \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\) से, या \(\frac{1}{20}=0.55\left(\frac{1}{R}+\frac{1}{R}\right)=\frac{0.55 \times 2}{R}\)
R = 2 × 0.55 × 20 = 22 सेमी।
अत: प्रत्येक पृष्ठ की वक्रता त्रिज्या 22 सेमी होनी चाहिए।
प्रश्न 8.
कोई प्रकाश पुंज किसी बिन्दु P पर अभिसरित होता है। कोई लेन्स इस अभिसारी पुंज के पथ में बिन्दु P से 12 सेमी दूर रखा जाता है। यदि यह
(a) 20 सेमी फोकस दूरी का उत्तल लेन्स है
(b) 16 सेमी फोकस दूरी का अवतल लेन्स है तो प्रकाश पुंज किस बिन्दु पर अभिसरित होगा?
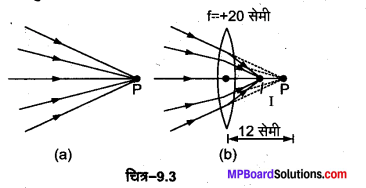
हल :
(a) स्पष्ट है कि इस स्थिति में बिन्दु P लेन्स के लिए आभासी वस्तु (बिम्ब) है।
∴ u = + 12 सेमी (लेन्स के दायीं ओर है), f= + 20 सेमी
∴लेन्स के सूत्र \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) से,
अतः \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}=\frac{1}{20}+\frac{1}{12}=\frac{3+5}{60}=\frac{8}{60}\)
⇒ v = \(\frac{60}{8}\) = 7.5 सेमी
अत: प्रकाश पुंज लेन्स के पीछे (दाहिनी ओर) लेन्स से 7.5 सेमी दूरी पर अभिसरित होगा।
(b) इस स्थिति में, f= – 16 सेमी
∴ \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}=-\frac{1}{16}+\frac{1}{12}=\frac{-3+4}{48}=\frac{1}{48}\)
⇒ v = + 48 सेमी
अतः प्रकाश पुंज लेन्स के दाहिनी ओर लेन्स से 48 सेमी दूरी पर अभिसरित होगा।
![]()
प्रश्न 9.
3.0 सेमी ऊँची कोई बिम्ब 21 सेमी फोकस दूरी के अवतल लेन्स के सामने 14 सेमी दूरी पर रखी है। लेन्स द्वारा निर्मित प्रतिबिम्ब का वर्णन कीजिए। क्या होता है जब बिम्ब लेन्स से दूर हटती जाती है?
हल :
दिया है, u = – 14 सेमी, f = – 21 सेमी, h = 3.0 सेमी
लेन्स के सूत्र \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) से,

अतः प्रतिबिम्ब 1.8 सेमी लम्बा आभासी तथा सीधा होगा, जो लेन्स के बायीं ओर उससे 8.4 सेमी की दूरी पर बनेगा।
जैसे-जैसे बिम्ब लेन्स से दूरी हटती है, (u → ∞) वैसे-वैसे प्रतिबिम्ब फोकस के समीप खिसकता जाता है (v → f)।
प्रश्न 10.
किसी 30 सेमी फोकस दूरी के उत्तल लेन्स के सम्पर्क में रखे 20 सेम फोकस दूरी के अवतल लेन्स के संयोजन से बने संयुक्त लेन्स (निकाय) की फोकस दूरी क्या है? यह तन्त्र अभिसारी लेन्स है अथवा अपसारी? लेन्सों की मोटाई की उपेक्षा कीजिए।
हल :
दिया है, f1= + 30 सेमी, f2 = – 20 सेमी
∴ \(\frac{1}{F}=\frac{1}{f_{1}}+\frac{1}{f_{2}}=\frac{1}{30}-\frac{1}{20}=\frac{2-3}{60}=-\frac{1}{60}\)
∴ संयुक्त लेन्स की फोकस दूरी F = – 60 सेमी
यह लेन्स अपसारी है।
प्रश्न 11.
किसी संयुक्त सूक्ष्मदर्शी में 2.0 सेमी फोकस दूरी का अभिदृश्यक लेन्स तथा 6.25 सेमी फोकस दूरी का नेत्रिका लेन्स एक-दूसरे से 15 सेमी दूरी पर लगे हैं। किसी बिम्ब को अभिदृश्यक से कितनी दूरी पर रखा जाए कि अन्तिम प्रतिबिम्ब
(a) स्पष्ट दृष्टि की अल्पतम दूरी (25 सेमी) तथा
(b) अनन्त पर बने? दोनों स्थितियों में सूक्ष्मदर्शी की आवर्धन क्षमता ज्ञात कीजिए।
हल :
(a) चूँकि नेत्रिका अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनाती है; अतः नेत्रिका के लिए
ve =- 25 सेमी, D = 25 सेमी, fe =+6.25 सेमी
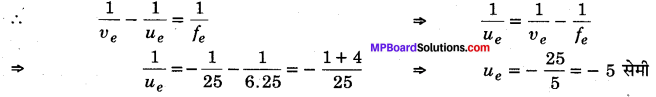
अतः अभिदृश्यक द्वारा बने प्रतिबिम्ब की नेत्रिका से दूरी = 5 सेमी
∴ इसकी अभिदृश्यक से दूरी = 15 – 5 = 10 सेमी (दायीं ओर) [∵ लेन्सों के बीच दूरी = 15 सेमी]
∴ अभिदृश्यक हेतु v0= + 10 सेमी, f 0= 2.0 सेमी
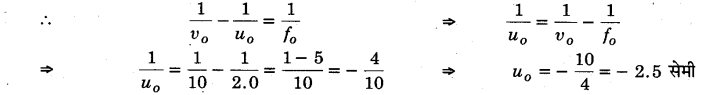
अतः बिम्ब को अभिदृश्यक के सामने 2.5 सेमी दूरी पर रखना होगा।
इस स्थिति में सूक्ष्मदर्शी की आवर्धन क्षमता M
∴ \(M=\frac{v_{o}}{\left|u_{o}\right|}\left(1+\frac{D}{f_{e}}\right)=\frac{10}{2.5}\left(1+\frac{25}{6.25}\right)=4 \times(1+4)=20\)
(b) इस स्थिति में, ve = ∞
\(\frac{1}{v_{e}}-\frac{1}{u_{e}}=\frac{1}{f_{e}}\) ⇒ \(0-\frac{1}{u_{e}}=\frac{1}{6.25}\)
⇒ ue = – 6.25 सेमी
∴ अभिदृश्यक द्वारा बने प्रतिबिम्ब की नेत्रिका से दूरी = 6.25 सेमी
∴ इसकी अभिदृश्यक से दूरी = 15- 6.25 = 8.75 सेमी
अतः अभिदृश्यक हेतु vo = + 8.75 सेमी, fo= 2.0 सेमी

अतः वस्तु को अभिदृश्यक के सामने 2.59 सेमी दूरी पर रखना होगा।
आवर्धन क्षमता \(M=\frac{v_{o}}{\left|u_{o}\right|} \times \frac{D}{f_{e}}=\frac{8.75}{2.59} \times \frac{25}{6.25}=13.5\)
प्रश्न 12.
25 सेमी के सामान्य निकट बिन्दु का कोई व्यक्ति ऐसे संयुक्त सूक्ष्मदर्शी जिसका अभिदृश्यक 8.0 मिमी फोकस दूरी तथा नेत्रिका 2.5 सेमी फोकस दूरी की है, का उपयोग करके अभिदृश्यक से 9.0 मिमी दूरी पर रखे बिम्ब को सुस्पष्ट फोकसित कर लेता है। दोनों लेन्सों के बीच पृथक्कन दूरी क्या है? सूक्ष्मदर्शी की आवर्धन क्षमता क्या है?
हल :
दिया है, fo = 8.0 मिमी fe= 0.8 सेमी, fo= 2.5 सेमी, u0 = – 9.0 मिमी = – 0.9 सेमी
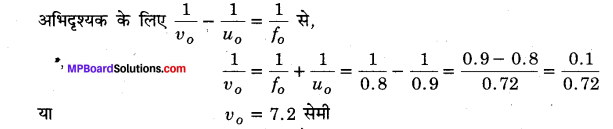
∴ व्यक्ति का निकट बिन्दु 25 सेमी है तथा व्यक्ति बिम्ब को स्पष्ट फोकसित कर लेता है, इसका यह अर्थ है कि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है।
अत: ve = – 25 सेमी, D = 25 सेमी
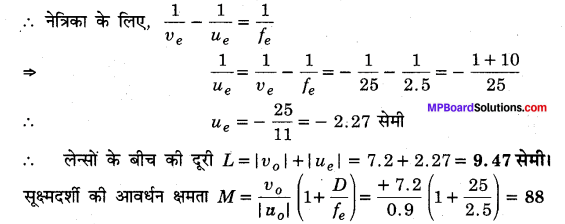
प्रश्न 13.
किसी छोटी दूरबीन के अभिदृश्यक की फोकस दूरी 144 सेमी तथा नेत्रिका की फोकस दूरी 6.0 सेमी है। दूरबीन की आवर्धन क्षमता कितनी है? अभिदृश्यक तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
हल :
दिया है, fo = 144 सेमी, fe = 6.0 सेमी
दूरबीन की आवर्धन क्षमता \(M=\frac{f_{0}}{f_{e}}=\frac{144}{6.0}\) = 24
दूरबीन की लम्बाई L= fo + fe = 144 + 6 = 150 सेमी।
प्रश्न 14.
(a) किसी वेधशाला की विशाल दूरबीन के अभिदृश्यक की फोकस दूरी 15 मीटर है। यदि 1.0 सेमी फोकस दूरी की नेत्रिका प्रयुक्त की गयी है तो दूरबीन का कोणीय आवर्धन क्या है?
(b) यदि इस दूरबीन का उपयोग चन्द्रमा का अवलोकन करने में किया जाए तो अभिदृश्यक लेन्स द्वारा निर्मित चन्द्रमा के प्रतिबिम्ब का व्यास क्या है? चन्द्रमा का व्यास 3.48x 106 मीटर तथा चन्द्रमा की कक्षा की त्रिज्या 3.8 x 108 मीटर है।
हल :
(a) दिया है : fo = 15 मीटर = 1500 सेमी, fe= 1.0 सेमी
∴ दूरबीन का कोणीय आवर्धन M = \(M=\frac{f_{o}}{f_{e}}=\frac{1500}{1.0}\) = 1500
(b) दिया है, चन्द्रमा का व्यास h = 3.48 × 106 मीटर
चन्द्रमा की वेधशाला से दूरी = 3.8 × 108 मीटर
माना अभिदृश्यक द्वारा बने प्रतिबिम्ब का व्यास d है.

∴ अभिदृश्यक द्वारा बने प्रतिबिम्ब का व्यास = 13.73 सेमी।
![]()
प्रश्न 15.
दर्पण-सूत्र का उपयोग यह व्युत्पन्न करने के लिए कीजिए कि
(a) किसी अवतल दर्पण के f तथा 2f के बीच रखे बिम्ब का वास्तविक प्रतिबिम्ब 26 से दूर बनता है।
(b) उत्तल दर्पण द्वारा सदैव आभासी प्रतिबिम्ब बनता है जो बिम्ब की स्थिति पर निर्भर नहीं करता।
(c) उत्तल दर्पण द्वारा सदैव आकार में छोटा प्रतिबिम्ब, दर्पण के ध्रुव व फोकस के बीच बनता है।
(d) अवतल दर्पण के ध्रुव तथा फोकस के बीच रखे बिम्ब का आभासी तथा बड़ा प्रतिबिम्ब बनता है।
हल :
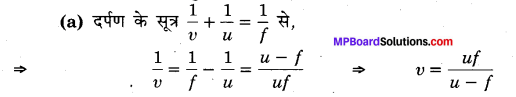
अवतल दर्पण के लिए f ऋणात्मक होता है जबकि u सभी दर्पणों के लिए ऋणात्मक है; अत: उक्त सूत्र से u व f को चिह्न सहित रखने पर,
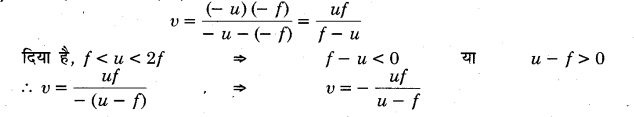
इससे स्पष्ट है कि v का मान ऋणात्मक है अर्थात् प्रतिबिम्ब दर्पण के सामने बनता है; अत: वास्तविक है।
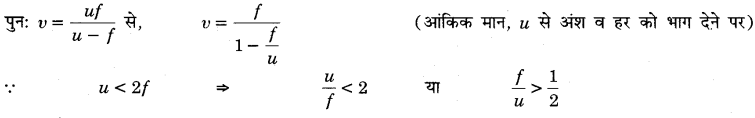
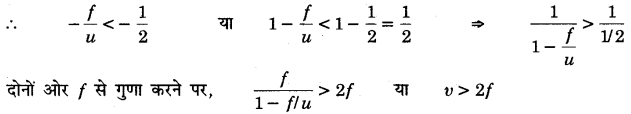
अर्थात् प्रतिबिम्ब 2f से दूर बनेगा।
(b) भाग (a) से, \(v=\frac{u f}{u-f}\)
उत्तल दर्पण के लिए f धनात्मक होता है जबकि u प्रत्येक दर्पण के लिए ऋणात्मक होता है; अत: चिह्न सहित मान रखने पर,

इससे स्पष्ट है कि v धनात्मक है अर्थात् प्रतिबिम्ब दर्पण के पीछे की ओर बनता है। अतः आभासी है।
इस प्रकार उत्तल दर्पण सदैव आभासी प्रतिबिम्ब बनाता है, जो बिम्ब की स्थिति पर निर्भर नहीं करता।
(c) पुनः भाग (b) के परिणाम से, \(v=\frac{u f}{u+f}\)
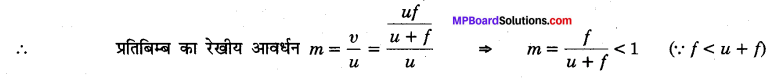
∵ रेखीय आवर्धन 1 से कम है; अत: स्पष्ट है कि प्रतिबिम्ब का आकार सदैव बिम्ब के आकार से छोटा है।
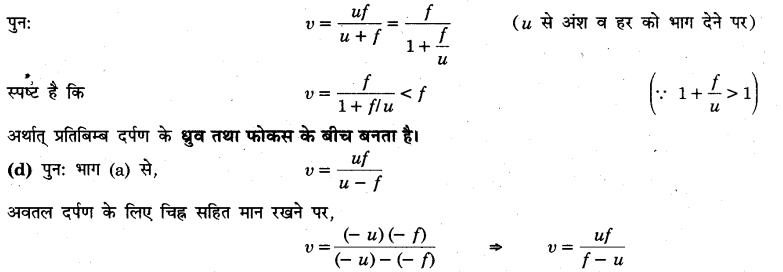
∵ बिम्ब ध्रुव तथा फोकस के बीच स्थित है; अत: 0 0
\(v=\frac{u f}{f-u}\) धनात्मक है।
\(m=\frac{v}{u}\) ⇒ (∵f – u < f)
∵ आवर्धन 1 से अधिक है, अर्थात् प्रतिबिम्ब का आकार वस्तु के आकार से बड़ा है।
प्रश्न 16.
किसी मेज के ऊपरी पृष्ठ पर जड़ी एक छोटी पिन को 50 सेमी ऊँचाई से देखा जाता है। 15 सेमी मोटे आयताकार काँच के गुटके को मेज के पृष्ठ के समान्तर पिन व नेत्र के बीच रखकर उसी बिन्दु से देखने पर पिन नेत्र से कितनी दूर दिखाई देगी? काँच का अपवर्तनांक 1.5 है। क्या उत्तर गुटके की अवस्थिति पर निर्भर करता है?
हल :
दिया है, ang = 1.5,
गुटके की वास्तविक मोटाई t= 15 सेमी तथा पिन की नेत्र से दूरी h = 50 सेमी
पिन से आँख तक पहुँचने वाली किरणें जब काँच के गुटके से होकर गुजरती हैं तो अपवर्तन के कारण गुटके की आभासी मोटाई वास्तविक मोटाई से कम प्रतीत होती है। इसी कारण पिन कुछ उठी हुई प्रतीत होती है।

अतः पिन 5 सेमी ऊपर उठी दिखाई देगी अर्थात् नेत्र से 45 सेमी गहराई पर दिखाई देगी।
छोटे अपवर्तन कोणों के लिए उत्तर गुटके की अवस्थिति पर निर्भर नहीं करता।
प्रश्न 17.
निम्नलिखित प्रश्नों के उत्तर लिखिए
(a) चित्र 9.4 में अपवर्तनांक 1.68 के तन्तु काँच से बनी किसी ‘प्रकाश नलिका’ (लाइट पाइप) का अनुप्रस्थ परिच्छेद दर्शाया गया है। नलिका का बाह्य आवरण 1.44 अपवर्तनांक के पदार्थ का बना है। नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते हैं, ज्ञात कीजिए।
(b) यदि पाइप पर बाह्य आवरण न हो तो क्या उत्तर होगा?
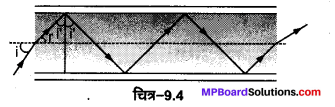
हल :
(a) बाह्य आवरण का अपवर्तनांक n1 = 1.44, तन्तु काँच का अपवर्तनांक n2= 1.68
बाह्य आवरण के सापेक्ष तन्तु काँच का अपवर्तनांक \(_{1} n_{2}=\frac{n_{2}}{n_{1}}=\frac{1.68}{1.44}=1.167\)
∵ n2 > n1
अत: तन्तु काँच, बाह्य आवरण के सापेक्ष सघन है।
अतः यदि कोई किरण तन्तु काँच में चलती हुई, सीमा पृष्ठ पर क्रान्तिक कोण i. से बड़े कोण पर आपतित होती है तो वह काँच में पूर्णतः परावर्तित हो जाएगी।
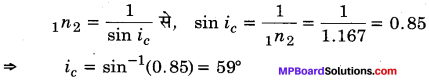
अत: पूर्ण आन्तरिक परावर्तन हेतु आपतन कोण i ऐसा होना चाहिए कि i> 59°
(b) इस स्थिति में तन्तु काँच के बाहर का माध्यम वायु होगा।
यदि काँच वायु के लिए क्रान्तिक कोण ic है तो \(n_{2}=\frac{1}{\sin i_{c}}\)
⇒ [latex]\sin i_{c}=\frac{1}{n_{2}}=\frac{1}{1.68}=0.59[/latex]
⇒ ic = sin-1(0.59) = 36°
अत: किरणों का आपतन कोण i> 36° होना चाहिए।
प्रश्न 18.
निम्नलिखित प्रश्नों के उत्तर लिखिए
(a) आपने सीखा है कि समतल तथा उत्तल दर्पण सदैव आभासी प्रतिबिम्ब बनाते हैं। क्या ये दर्पण किन्हीं परिस्थितियों में वास्तविक प्रतिबिम्ब बना सकते हैं? स्पष्ट कीजिए।
(b) हम सदैव कहते हैं कि आभासी प्रतिबिम्ब को परदे पर केन्द्रित नहीं किया जा सकता। यद्यपि जब हम किसी आभासी प्रतिबिम्ब को देखते हैं तो हम इसे स्वाभाविक रूप में अपनी आँख की स्क्रीन (अर्थात् रेटिना) पर लेते हैं। क्या इसमें कोई विरोधाभास है?
(c) किसी झील के तट पर खड़ा मछुआरा झील के भीतर किसी गोताखोर द्वारा तिरछा देखने पर अपनी वास्तविक लम्बाई की तुलना में कैसा प्रतीत होगा-छोटा अथवा लम्बा?
(d) क्या तिरछा देखने पर किसी जल के टैंक की आभासी गहराई परिवर्तित हो जाती है? यदि हाँ, तो आभासी गहराई घटती है अथवा बढ़ जाती है।
(e) सामान्य काँच की तुलना में हीरे का अपवर्तनांक काफी अधिक होता है? क्या हीरे को तराशने वालों के लिए इस तथ्य का कोई उपयोग होता है?
उत्तर :
(a) यह सही है कि समतल दर्पण तथा उत्तल दर्पण अपने सामने स्थित बिम्ब का आभासी प्रतिबिम्ब बनाते हैं। परन्तु ये दर्पण अपने पीछे स्थित किसी बिन्दु (आभासी बिम्ब) की ओर अभिसरित किरण पुंज को परावर्तित करके अपने सामने स्थित किसी बिन्दु पर अभिसरित कर सकते हैं अर्थात् आभासी बिम्ब का वास्तविक प्रतिबिम्ब बन सकते हैं [देखें चित्र-9.5 (a)]।
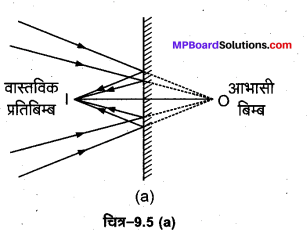
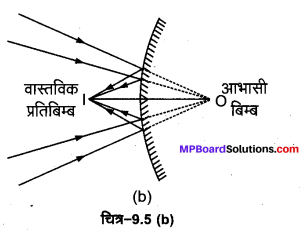
(b) जब किसी दर्पण से परावर्तन अथवा लेन्स से अपवर्तन के पश्चात् किरणें अपसरित होती हैं तो प्रतिबिम्ब को आभासी कहा जाता है। इस प्रतिबिम्ब को परदे पर प्राप्त नहीं किया जा सकता। यदि इन अपसारी किरणों के मार्ग में कोई अन्य दर्पण अथवा लेन्स रखकर इन्हें किसी बिन्दु पर अभिसरित किया जा सकता तो वहाँ वास्तविक प्रतिबिम्ब बनेगा जिसे परदे पर प्राप्त किया जा सकता है। नेत्र लेन्स वास्तव में यही कार्य करता है। यह आभासी प्रतिबिम्ब बनाने वाली अपसारी किरणों को रेटिना पर अभिसरित कर देता है, जहाँ वास्तविक प्रतिबिम्ब बन जाता है। अतः इसमें कोई विरोधाभास नहीं है [देखें चित्र-9.5 (b)]।
(c) चूँकि इस दशा में अपवर्तन वायु (विरल माध्यम) से पानी (सघन माध्यम) में होता है। अतः झील में डूबे हुए गोताखोर को मछुआरे की लम्बाई अधिक प्रतीत होगी।
(d) हाँ, परिवर्तित हो जाती है। यह आभासी गहराई घट जाती है।
(e) वायु के सापेक्ष हीरे का अपवर्तनांक 2.42 (काफी अधिक) है तथा क्रान्तिक कोण 24° (बहुत कम) है। हीरा तराशने में दक्ष कारीगर इस तथ्य का उपयोग करते हुए हीरे को इस प्रकार तराशता है कि एक बार हीरे में प्रवेश करने वाली प्रकाश किरण हीरे के विभिन्न फलकों पर बार-बार परावर्तित होने के बाद ही किसी फलक से बाहर निकल पाए। इसके लिए हीरे की आन्तरिक सतह पर आपतन कोण 24° से अधिक होना चाहिए। इससे हीरा अत्यधिक चमकीला दिखाई पड़ता है।
![]()
प्रश्न 19.
किसी कमरे की एक दीवार पर लगे विद्युत बल्ब का किसी बड़े आकार के उत्तल लेन्स द्वारा 3 मीटर दूरी पर स्थित सामने की दीवार पर प्रतिबिम्ब प्राप्त करना है। इसके लिए उत्तल लेन्स की अधिकतम फोकस दूरी क्या होनी चाहिए?
हल :
माना किसी उत्तल लेन्स की फोकस दूरी f है तथा यह बल्ब का प्रतिबिम्ब दूसरी दीवार पर बनाता है।
माना बल्ब की लेन्स से दूरी u (आंकिक मान) तथा दूसरी दीवार की लेन्स से दूरी v है, तब
u + v = 3 ⇒ u = 3 – v
लेन्स के सूत्र में चिह्न सहित मान रखने पर,

उक्त समीकरण v के वास्तविक मान देगा यदि
B2 ≥ 4AC या (-3)2 ≥ 4 × 3f या 9 ≥ 12f
⇒ [latex]f \leq \frac{9}{12}=\frac{3}{4}[/latex]
∴ लेन्स की अधिकतम फोकस दूरी fmax = \(\frac{3}{4}\) मीटर = 75 सेमी।
प्रश्न 20.
किसी परदे को बिम्ब से 90 सेमी दूर रखा गया है। परदे पर किसी उत्तल लेन्स द्वारा उसे एक-दूसरे से 20 सेमी दूर स्थितियों पर रखकर, दो प्रतिबिम्ब बनाए जाते हैं। लेन्स की फोकस दूरी ज्ञात कीजिए।
हल :
माना बिम्ब की लेन्स से दूरी u (आंकिक मान) है तथा प्रतिबिम्ब (परदे) की लेन्स से दूरी v है।
तब u+ v = 90 ⇒ v = 90-u
लेन्स के सूत्र में चिह्न सहित मान रखने पर,
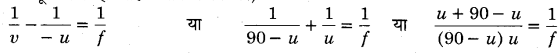
⇒ 90f = (90 – u) u या u2 – 90u + 90f = 0 ……………………….(1)
चूँकि लेन्स दो स्थितियों में वस्तु का प्रतिबिम्ब परदे पर बनाता है तथा दो स्थितियों के बीच की दूरी 20 सेमी है;
अत: समीकरण (1) में u में दो मूल (माना u1 व u2) होंगे जिनका अन्तर 20 सेमी होगा।
अर्थात् (u1 – u2)2 = (20)2 = 400
समीकरण (1) से, u1 + u2 = 90 ⇒ u1u2= 90f
∴(u1 – u2)2 = (u1 + u2)2 – 4u1u2
⇒ 400 = (90)2 – 4 × 90f ⇒ 360f = 8100 – 400 = 7700
∴ फोकस दूरी \(f=\frac{7700}{360}\) = 21.38 ≈ 21.4 सेमी।
अन्य विधि-विस्थापन विधि के सूत्र से, \(f=\frac{a^{2}-d^{2}}{4 a}\)
यहाँ a = बिम्ब तथा प्रतिबिम्ब के बीच की दूरी = 90 सेमी
d = लेन्स की दो स्थितियों के बीच की दूरी = 20 सेमी
∴ फोकस दरी\(f=\frac{(90)^{2}-(20)^{2}}{4 \times 90}=\frac{8100-400}{360}=\frac{7700}{360}\) = 21.4 सेमी।
प्रश्न 21.
(a) प्रश्न 10 के दो लेन्सों के संयोजन की प्रभावी फोकस दूरी उस स्थिति में ज्ञात कीजिए जब उनके मुख्य अक्ष संपाती हैं तथा ये एक-दूसरे से 8 सेमी दूरी पर रखे हैं। क्या उत्तर आपतित समान्तर प्रकाश पुंज की दिशा पर निर्भर करेगा? क्या इस तन्त्र के लिए प्रभावी फोकस दूरी किसी भी रूप में उपयोगी है?
(b) उपर्युक्त व्यवस्था (a) में 1.5 सेमी ऊँचा कोई बिम्ब उत्तल लेन्स की ओर रखा है। बिम्ब की उत्तल लेन्स से दूरी 40 सेमी है। दो लेन्सों के तन्त्र द्वारा उत्पन्न आवर्धन तथा प्रतिबिम्ब का आकार ज्ञात कीजिए।
हल :
(a) लेन्सों की फोकस दूरियाँ f1 = + 30 सेमी, f2 = – 20 सेमी
कल्पना करें कि एक समान्तर किरण पुंज बाईं ओर से उत्तल लेन्स पर आपतित होता है, तब उत्तल लेन्स हेतु
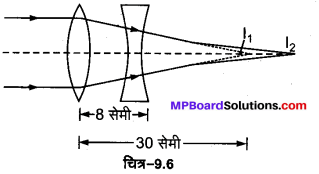
u = – ∞
∴ \(\frac{1}{v}-\frac{1}{-\infty}=\frac{1}{f_{1}}\)
⇒ v = f1 = + 30 सेमी
अर्थात् उत्तल लेन्स इन किरणों को 30 सेमी की दूरी पर बिन्दु I पर मिलाता है।
बिन्दु I1 अवतल लेन्स के लिए आभासी बिम्ब है।
∴ अवतल लेन्स हेतु, u = (30- 8) = + 22 सेमी
![]()
⇒ v = – 220 सेमी
अर्थात् अन्तिम प्रतिबिम्ब, अवतल लेन्स के बाईं ओर इससे 220 सेमी दूर बनता है।
इस प्रतिबिम्ब की लेन्सों के केन्द्र से दूरी 220 – \(\frac{8}{2}\) =216 सेमी है।
अर्थात् अवतल लेन्स की ओर से देखने पर यह किरण पुंज लेन्सों के केन्द्र से 216 सेमी बाईं ओर स्थित बिन्दु से अपसरित प्रतीत होता है।
इस प्रकार यदि इस युग्म की फोकस दूरी अर्थपूर्ण है तो यह फोकस दूरी – 216 सेमी होनी चाहिए।
दूसरी दशा में कल्पना कीजिए कि समान्तर किरण पुंज दाईं ओर से चलता हुआ पहले अवतल लेन्स पर आपतित होता है।
∴ अवतल लेन्स हेतु u = – ∞
∴ \(\frac{1}{v}-\frac{1}{-\infty}=\frac{1}{-20}\) ⇒ v = – 20 सेमी
अर्थात् अवतल लेन्स से अपवर्तन के कारण ये किरणें उसके पीछे 20 सेमी दूरी पर स्थित बिन्दु से आती प्रतीत होती हैं। यह बिन्दु उत्तल लेन्स हेतु आभासी बिम्ब का कार्य करेगा।
∴ उत्तल लेन्स हेतु u = – (20 + 8) = – 28

अर्थात् उत्तल लेन्स की ओर से देखने पर किरणें इससे पीछे की ओर 420 सेमी दूरी पर स्थित बिन्दु से आती प्रतीत होती हैं।
इस बिन्दु की निकाय के केन्द्र से दूरी 420 – \(\frac{8}{2}\) = 416 सेमी है।
∴ निकाय की फोकस दूरी – 416 सेमी होनी चाहिए।
इस प्रकार हम देखते हैं कि इस निकाय की फोकस दूरी आपतित किरण पुंज की दिशा पर निर्भर करती हैं; अत: यह फोकस दूरी किसी भी रूप में उपयोगी नहीं है।
(b) उत्तल लेन्स हेतु U1 = – 40 सेमी, f1 = + 30 सेमी, h = 1.5 सेमी

∴ अवतल लेन्स हेतु u2 = + (v1 – 8)= + 112 सेमी
जबकि f2 = – 20 सेमी
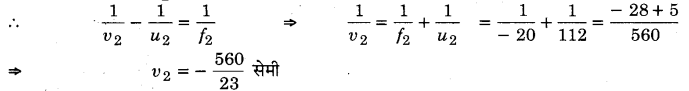
∴ तन्त्र द्वारा उत्पन्न आवर्धन m = m1 × m2 = \(\frac{v_{1}}{u_{1}} \times \frac{v_{2}}{u_{2}}=\frac{+120}{-40} \times \frac{-560 / 23}{112}\)
m = \(\frac{15}{23}\) = 0.652
m =\( \frac{h^{\prime}}{h}\) से,
h’ = h × m = 1.5 × 0.652 = 0.98 सेमी
अत:” प्रतिबिम्ब का आकार = 0.98 सेमी।
![]()
प्रश्न 22.
60° अपवर्तन कोण के प्रिज्म के फलक पर किसी प्रकाश किरण को किस कोण पर आपतित कराया जाए कि इसका दूसरे फलक से केवल पूर्ण आन्तरिक परावर्तन ही हो? प्रिज्म के पदार्थ का अपवर्तनांक 1.524 है।
हल :
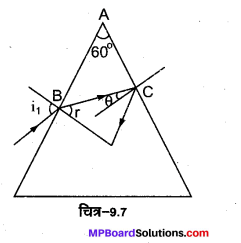
A= 60°, ang = 1.524
चित्र से, 90° – r +90° – θ + 60° = 180° (∆ABC में)
r = 60° – θ
यदि θ = ic हो तो r = 60° – ic
जबकि \(\sin i_{c}=\frac{1}{a^{n} g}=\frac{1}{1.524}=0.656\) ⇒ ic = sin-1(0.656) = 41
अतः r = 60° – 41° = 19°
अतः बिन्दु B पर अपवर्तन हेतु \(a n_{g}=\frac{\sin i}{\sin r}\)
⇒ sin i = ang × sin r
या sin i = 1.524 × sin 19° = 0.5 = \(\frac { 1 }{ 2 }\) =sin 30°.
अतः i= 30°
दूसरे फलक से पूर्ण आन्तरिक परावर्तन के लिए आवश्यक है कि किरण इस फलक पर क्रान्तिक कोण icसे बड़े कोण पर गिरे।
∵ r = 60° – θ तथा θ = ic के लिए, r = 19°, i = 30°
∴ θ > ic के लिए, r < 19° = i< 30°
अत: दूसरे फलक से पूर्ण आन्तरिक परावर्तन हेतु आपतन कोण i < 30°
प्रश्न 23.
आपको विविध कोणों के क्राउन काँच व फ्लिण्ट काँच के प्रिज्म दिए गए हैं। प्रिज्मों का कोई ऐसा संयोजन सुझाइए जो
(a) श्वेत प्रकाश के संकीर्ण पंज को बिना अधिक परिक्षेपित किए विचलित कर दे।
(b) श्वेत प्रकाश के संकीर्ण पुंज को अधिक विचलित किए बिना परिक्षेपित (तथा विस्थापित) कर दे।
उत्तर :
हम जानते हैं कि फ्लिण्ट काँच, क्राउन काँच की तुलना में अधिक विक्षेपण उत्पन्न करता है।
(a) बिना विक्षेपण के विचलन उत्पन्न करने हेतु क्राउन काँच का एक प्रिज्म लीजिए तथा एक फ्लिण्ट काँच का प्रिज्म लीजिए जिसका अपवर्तक कोण अपेक्षाकृत कम हो। अब इन्हें एक-दूसरे के सापेक्ष उल्टा रखते हुए सम्पर्क में रखिए। इस प्रकार बना संयोजन श्वेत प्रकाश को बिना अधिक परिक्षेपित किए विचलित कर देगा।
(b) पुराने संयोजन में लिए गए फ्लिण्ट काँच के प्रिज्म के अपवर्तक कोण में वृद्धि कीजिए (परन्तु अभी भी यह कोण दूसरे प्रिज्म की तुलना में कम ही रहेगा)। यह व्यवस्था पुंज को बिना अधिक विचलित किए परिक्षेपण उत्पन्न करेगी।
प्रश्न 24.
सामान्य नेत्र के लिए दूर बिन्दु अनन्त पर तथा स्पष्ट दर्शन का निकट बिन्दु नेत्र के सामने लगभग 25 सेमी पर होता है। नेत्र का स्वच्छ मण्डल (कॉर्निया) लगभग 40 D की अभिसरण क्षमता प्रदान करता है तथा स्वच्छ मण्डल के पीछे नेत्र लेन्स की अल्पतम अभिसरण क्षमता लगभग 20 D होती है। इस स्थूल आँकड़े से सामान्य नेत्र के परास (अर्थात् नेत्र लेन्स की अभिसरण क्षमता का परिसर) का अनुमान लगाइए।
हल :
नेत्र लेन्स की अल्पतम अभिसरण क्षमता P1 = + 20 D
जबकि कॉर्निया की अभिसरण क्षमता P2 = + 40 D
जब वस्तु अनन्त पर होती है तो नेत्र न्यूनतम क्षमता का प्रयोग करके, अनन्त पर स्थित बिन्दु का प्रतिबिम्ब दृष्टि पटल पर बनाता है।
इस समय नेत्र की क्षमता P = P1 + P2= 60 D
∴ फोकस दूरी f = \(\frac{100}{P}\) सेमी = \(\frac{100}{60}\) = \(\frac{5}{3}\) सेमी
यदि दृष्टि पटल की लेन्स से दूरी v है तो u =∞, f = \(\frac{5}{3}\) सेमी से,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) ⇒ \(\frac{1}{v}-\frac{1}{-\infty}=\frac{3}{5}\)
∴ दृष्टि पटल की लेन्स से दूरी v = \(\frac{5}{3}\) सेमी
जब वस्तु नेत्र के निकट बिन्दु (25 सेमी दूरी) पर होती है तो नेत्र सम्पूर्ण अभिसरण क्षमता का प्रयोग करता है।
माना इस दशा में नेत्र लेन्स की अभिसरण क्षमता = P1‘
जबकि सम्पूर्ण नेत्र की फोकस दूरी माना f’ है, तब \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f^{\prime}}\)
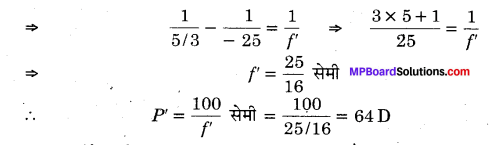
परन्तु कॉर्निया की अभिसरण क्षमता + 40D नियत है,
∴ नेत्र लेन्स की अधिकतम अभिसरण क्षमता P1‘ = P’ – P2 = 64- 40 = + 24 D [∵ P’ = P’1 + P2]
अत: नेत्र लेन्स की अभिसरण परास + 20D से + 24 D के बीच है।
![]()
प्रश्न 25.
क्या निकट दृष्टिदोष अथवा दीर्घ दृष्टिदोष आवश्यक रूप से यह ध्वनित होता है कि नेत्र ने अपनी समंजन क्षमता आंशिक रूप से खो दी है? यदि नहीं, तो इन दृष्टिदोषों का क्या कारण हो सकता है?
हल :
यह आवश्यक नहीं है कि निकट दृष्टिदोष अथवा दूर दृष्टिदोष केवल नेत्र के आंशिक रूप से अपनी समंजन क्षमता खो देने के कारण ही उत्पन्न होता है। यह नेत्र गोलक के सामान्य आकार से बड़ा अथवा छोटा होने के कारण भी उत्पन्न हो सकता है।
प्रश्न 26.
निकट दृष्टिदोष का कोई व्यक्ति दूर दृष्टि के लिए – 1D क्षमता का चश्मा उपयोग कर रहा है। अधिक आयु होने पर उसे पुस्तक पढ़ने के लिए अलग से + 2.0 D क्षमता के चश्मे की आवश्यकता होती है। स्पष्ट कीजिए ऐसा क्यों हुआ?
हल :
∴ P= – 1.0D
∴f = \(\frac{100}{P}\) सेमी = \(\frac{100}{1.0}\) = – 100 सेमी
इससे स्पष्ट है कि व्यक्ति का दूर बिन्दु 100 सेमी की दूरी पर आ गया है। इस दशा में अनन्त पर स्थित वस्तुओं को देखने के लिए वह ऐसे चश्मे (-1.0 D) का प्रयोग करता है जो अनन्त पर स्थित वस्तु का प्रतिबिम्ब 100 सेमी की दूरी पर बना देता है।
इससे पास की वस्तुओं (25 सेमी व 100 सेमी के बीच की) को मनुष्य, नेत्र की समंजन क्षमता का प्रयोग करके देख लेता है। उम्र के बढ़ने के साथ-साथ उसके नेत्र की समंजन क्षमता भी कम हो जाती है। इस कारण उसे निकट की वस्तुओं को देखने के लिए भी चश्मे की आवश्यकता होती है।
प्रश्न 27.
कोई व्यक्ति ऊर्ध्वाधर तथा क्षैतिज धारियों की कमीज पहने किसी दूसरे व्यक्ति को देखता है। वह क्षैतिज धारियों की तुलना में ऊर्ध्वाधर धारियों को अधिक स्पष्ट देख पाता है। ऐसा किस दृष्टिदोष के कारण होता है? इस दृष्टिदोष का संशोधन कैसे किया जाता है?
हल :
यह घटना अबिन्दुकता नामक दृष्टिदोष के कारण होती है। सामान्य नेत्र पूर्णतः गोलीय होता है तथा इसके विभिन्न तलों की वक्रता सर्वत्र समान होती है। परन्तु अबिन्दुकता दोष में कॉर्निया पूर्णतः गोलीय नहीं रह जाता तथा इसके विभिन्न तलों की वक्रताएँ समान नहीं रह पातीं। प्रश्नानुसार व्यक्ति ऊर्ध्वाधर धारियों को स्पष्ट देख पाता है परन्तु क्षैतिज धारियों को नहीं। इससे स्पष्ट है कि नेत्र में ऊर्ध्वाधर तल में पर्याप्त वक्रता है जिसके कारण ऊर्ध्वाधर रेखाएँ दृष्टि पटल पर स्पष्ट फोकस हो रही हैं। परन्तु क्षैतिज तल की वक्रता पर्याप्त नहीं है।
इस दोष को सिलिण्डरी लेन्स की सहायता से दूर किया जा सकता है।
प्रश्न 28.
कोई सामान्य निकट बिन्दु ( 25 सेमी) का व्यक्ति छोटे अक्षरों में छपी वस्तु को 5 सेमी फोकस दूरी के पतले उत्तल लेन्स के आवर्धक लेन्स का उपयोग करके पढ़ता है।
(a) वह निकटतम तथा अधिकतम दूरियाँ ज्ञात कीजिए जहाँ वह उस पुस्तक को आवर्धक लेन्स द्वारा पढ़ सकता है।
(b) उपर्युक्त सरल सूक्ष्मदर्शी के उपयोग द्वारा सम्भावित अधिकतम तथा न्यूनतम कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
हल :
(a) दिया है, f = + 5 सेमी
निकटतम दूरी वह दूरी होगी जबकि लेन्स पुस्तक का प्रतिबिम्ब मनुष्य के निकट बिन्दु पर बनाएगा।
इसके लिए v = – 25 सेमी

पुनः अधिकतम दूरी वह दूरी होगी, जबकि लेन्स वस्तु का प्रतिबिम्ब अनन्त पर बनाएगा।
इसके लिए v = ∞.
∴ \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) ⇒ \(\frac{1}{\infty}-\frac{1}{u}=\frac{1}{5}\)
⇒ u = – 5 सेमी
अतः निकटतम दूरी = 4\(\frac{1}{2}\) सेमी तथा अधिकतम दूरी = 5 सेमी।
(b) अधिकतम कोणीय आवर्धन mmax = 1 + \(\frac{D}{f}\) = 1 + \(\frac{25}{5}\) = 6
न्यूनतम कोणीय आवर्धन mmin = \(\frac{D}{f}\) = \(\frac{25}{5}\) = 5
प्रश्न 29.
कोई कार्ड शीट जिसे 1 मिमी2 साइज के वर्गों में विभाजित किया गया है, को 9 सेमी दूरी पर रखकर किसी आवर्धक लेन्स (10 सेमी फोकस दूरी का अभिसारी लेन्स) द्वारा उसे नेत्र के निकट रखकर देखा जाता है।
(a) लेन्स द्वारा उत्पन्न आवर्धन (प्रतिबिम्ब-साइज/ वस्तु-साइज) क्या है? आभासी प्रतिबिम्ब में प्रत्येक वर्ग का . क्षेत्रफल क्या है?
(b) लेन्स का कोणीय आवर्धन (आवर्धन क्षमता) क्या है?
(c) क्या (a) में आवर्धन (b) में आवर्धन के बराबर है? स्पष्ट कीजिए।
हल :
(a) ∵ u = – 9 सेमी, f= + 10 सेमी

⇒ 10 = \(\frac{h^{\prime}}{h}\) ⇒ h’ = 10h = 10 × 1 मिमी = 1 सेमी ::
∴ प्रतिबिम्ब के प्रत्येक वर्ग का क्षेत्रफल = h’ × h’ = 1 सेमी2।
(b) लेन्स का कोणीय आवर्धन (आवर्धन क्षमता) \(m=\frac{D}{f}=\frac{25}{10}=2.5\)
(c) नहीं, किसी लेन्स द्वारा उत्पन्न आवर्धन तथा लेन्स की आवर्धन क्षमता दोनों अलग-अलग अवधारणाएँ हैं। .
लेन्स द्वारा उत्पन्न आवर्धन, प्रतिबिम्ब के आकार तथा वस्तु के आकार के अनुपात के बराबर होता है। अत: \frac{v}{u} के बराबर होता है जबकि प्रकाशिक यन्त्र की आवर्धन क्षमता उसके द्वारा बने अन्तिम प्रतिबिम्ब के कोणीय साइज तथा वस्तु के कोणीय साइज के अनुपात के बराबर होता है जबकि वस्तु आँख के निकट बिन्दु पर रखी गई है।
उक्त दोनों राशियाँ केवल तभी बराबर होती हैं जबकि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है।
![]()
प्रश्न 30.
(a) प्रश्न 29 में लेन्स को चित्र से कितनी दूरी पर रखा जाए ताकि वर्गों को अधिकतम सम्भव आवर्धन क्षमता के साथ सुस्पष्ट देखा जा सके।
(b) इस उदाहरण में आवर्धन (प्रतिबिम्ब-साइज/ वस्तु-साइज़) क्या है?
(c) क्या इस प्रक्रम में आवर्धन, आवर्धन क्षमता के बराबर है? स्पष्ट कीजिए।
हल :
(a) किसी आवर्धक लेन्स द्वारा अधिकतम आवर्धन तब प्राप्त होता है जबकि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है।
इस स्थिति में v = – 25 सेमी, f= 10 सेमी

(b) इस दशा में आवर्धन का परिमाण = \(\frac{v}{u}=\frac{25}{7.14}=3.5\)
(c) आवर्धन क्षमता = \(\frac{D}{u}=\frac{25}{7.14}=3.5\)
हाँ, इस दशा में दोनों राशियाँ बराबर हैं। ऐसा इसलिए सम्भव हुआ है क्योंकि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बना है।
प्रश्न 31.
प्रश्न 30 में वस्तु तथा आवर्धक लेन्स के बीच कितनी दूरी होनी चाहिए ताकि आभासी प्रतिबिम्ब में प्रत्येक वर्ग 6.25 मिमी2 क्षेत्रफल का प्रतीत हो? क्या आप आवर्धक लेन्स को नेत्र के अत्यधिक निकट रखकर इन वर्गों को सुस्पष्ट देख सकेंगे।
हल
∵ वर्ग का क्षेत्रफल = 1.0 मिमी2
वर्ग के प्रतिबिम्ब का क्षेत्रफल = 6.25 मिमी2

∴ वस्तु को लेन्स से 6 सेमी दूरी पर रखना होगा।
इस स्थिति में आभासी प्रतिबिम्ब नेत्र के निकट बिन्दु से भी पहले बनेगा; अतः उसे स्पष्ट देख पाना सम्भव नहीं होगा।
प्रश्न 32.
निम्नलिखित प्रश्नों के उत्तर दीजिए –
(a) किसी वस्तु द्वारा नेत्र पर अन्तरित कोण आवर्धक लेन्स द्वारा उत्पन्न आभासी प्रतिबिम्ब द्वारा नेत्र पर अन्तरित कोण के बराबर होता है। तब फिर इन अर्थों में कोई आवर्धक लेन्स कोणीय आवर्धन प्रदान करता है।
(b) किसी आवर्धक लेन्स से देखते समय प्रेक्षक अपने नेत्र को लेन्स से अत्यधिक सटाकर रखता है। यदि प्रेक्षक अपने नेत्र को पीछे ले जाए तो क्या कोणीय आवर्धन परिवर्तित हो जाएगा?
(c) किसी सरल सूक्ष्मदर्शी की आवर्धन क्षमता उसकी फोकस दूरी के व्युत्क्रमानुपाती होती है। तब हमें अधिकाधिक आवर्धन क्षमता प्राप्त करने के लिए कम-से-कम फोकस दूरी के उत्तल लेन्स का उपयोग करने से कौन रोकता है?
(d) किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक लेन्स तथा नेत्रिका लेन्स दोनों ही की फोकस दूरी कम क्यों होनी चाहिए?
(e) संयुक्त सूक्ष्मदर्शी द्वारा देखते समय सर्वोत्तम दर्शन के लिए हमारे नेत्र, नेत्रिका पर स्थित न होकर उससे कुछ दूरी पर होने चाहिए। क्यों? नेत्र तथा नेत्रिका के बीच की यह अल्प दूरी कितनी होनी चाहिए?
उत्तर :
(a) आवर्धक लेन्स के बिना वस्तु को देखते समय उसे नेत्र से 25 सेमी से कम दूरी पर नहीं रखा जा सकता, परन्तु लेन्स की सहायता से वस्तु को देखते समय वस्तु को अपेक्षाकृत नेत्र के अधिक समीप रखा जा सकता है जिससे कि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने। इस प्रकार कोणीय साइज में वृद्धि वस्तु को नेत्र के समीप रखने के कारण होती है।
(b) हाँ, क्योंकि इस स्थिति में प्रतिबिम्ब द्वारा नेत्र पर बना दर्शन कोण, उसके द्वारा लेन्स पर बने दर्शन कोण से कुछ छोटा हो जाएगा।
(c) एक-तो अत्यन्त कम फोकस दूरी के लेन्सों (मोटे लेन्सों) को बनाने की प्रक्रिया आसान नहीं है, दूसरे फोकस दूरी घटने के साथ लेन्सों में विपथन का दोष बढ़ने लगता है। इससे उनके द्वारा बने प्रतिबिम्ब अस्पष्ट हो जाते हैं। व्यवहार में किसी एकल उत्तल लेन्स द्वारा 3 से अधिक आवर्धन प्राप्त करना सम्भव नहीं है परन्तु विपथन के दोष से मुक्त लेन्स द्वारा कहीं अधिक आवर्धन (लगभग 10) प्राप्त किया जा सकता है।
(d) सूक्ष्मदर्शी के अभिदृश्यक का आवर्धन \(\frac{v_{o}}{\left|u_{o}\right|}=\frac{1}{\left(\frac{\left|u_{o}\right|}{f_{o}}-1\right)}\) होता है। इससे स्पष्ट है कि इस आवर्धन को बढ़ाने के लिए | u0| का मान f0 से कुछ अधिक होना चाहिए। परन्तु सूक्ष्मदर्शी समीप की वस्तुओं को देखने के लिए प्रयोग किया जाता है जो अभिदृश्यक के समीप रखी जाती हैं। अतः इन वस्तुओं के लिए | u0 | का मान कम होता है, इसलिए f0 का मान और भी कम रखना पड़ता है।
नेत्रिका का आवर्धन \(\left(1+\frac{D}{f_{e}}\right)\) होता है; अतः स्पष्ट है कि इसे बढ़ाने के लिए fe का मान कम रखा जाता है।
(e) संयुक्त सूक्ष्मदर्शी में वस्तु से चलने वाला प्रकाश अभिदृश्यक से गुजरने के बाद नेत्रिका से गुजरकर आँख तक पहुँचता है। वस्तु का प्रतिबिम्ब स्पष्ट देखने के लिए आवश्यक है कि वस्तु से चलने वाला अधिकतम प्रकाश नेत्र में पहुँचे। वस्तु से चलने वाले प्रकाश को अधिकतम मात्रा में ग्रहण करने के लिए ही नेत्र को नेत्रिका से अत्यल्प दूरी पर रखा जाता है। यह अत्यल्प दूरी यन्त्र की संरचना पर निर्भर करती है तथा उस पर लिखी गई होती है।
प्रश्न 33.
1.25 सेमी फोकस दूरी का अभिदृश्यक तथा 5 सेमी फोकस दूरी की नेत्रिका का उपयोग करके वांछित कोणीय आवर्धन (आवर्धन क्षमता) 30 होता है। आप संयुक्त सूक्ष्मदर्शी का समायोजन कैसे करेंगे?
हल : संयुक्त सूक्ष्मदर्शी के लिए, f0 = 1.25 सेमी, fe = 5 सेमी, आवर्धन क्षमता = 30
माना सूक्ष्मदर्शी सामान्य उपयोग में है (अन्तिम प्रतिबिम्ब निकट बिन्दु पर है) तब

∴ सूक्ष्मदर्शी की लम्बाई L = v0+ ue = 7.5 + 4.17 ⇒ L= 11.67 सेमी
अतः वस्तु को अभिदृश्यक से 1.5 सेमी की दूरी पर रखना चाहिए तथा नेत्रिका की अभिदृश्यक से दूरी 11.67 सेमी रखनी चाहिए।
![]()
प्रश्न 34.
किसी दूरबीन के अभिदृश्यक की फोकस दूरी 140 सेमी तथा नेत्रिका की फोकस दूरी 5.0 सेमी है। दूर की वस्तुओं को देखने के लिए दूरबीन की आवर्धन क्षमता क्या होगी जब
(a) दूरबीन का समायोजन सामान्य है ( अर्थात् अन्तिम प्रतिबिम्ब अनन्त पर बनता है)।
(b) अन्तिम प्रतिबिम्ब स्पष्ट दर्शन की अल्पतम दूरी ( 25 सेमी) पर बनता है।
हल :
दूरदर्शी हेतु f0 = 140 सेमी, fe= 5.0 सेमी .
(a) जब अन्तिम प्रतिबिम्ब अनन्त पर है तब आवर्धन क्षमता \(M = \frac{f_{o}}{f_{e}}=\frac{140}{5}=28\)
(b) जब अन्तिम प्रतिबिम्ब निकट बिन्दु पर है तब आवर्धन क्षमता \(M=\frac{f_{0}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)=\frac{140}{5}\left(1+\frac{5.0}{25}\right)=33.6\)
प्रश्न 35.
(a) प्रश्न 34 (a) में वर्णित दूरबीन के लिए अभिदृश्यक लेन्स तथा नेत्रिका के बीच पृथक्कन दूरी क्या है?
(b) यदि इस दूरबीन का उपयोग 3 किमी दूर स्थित 100 मीटर ऊँची मीनार को देखने के लिए किया जाता है तो अभिदृश्यक द्वारा बने मीनार के प्रतिबिम्ब की ऊँचाई क्या है?
(c) यदि अन्तिम प्रतिबिम्ब 25 सेमी दूर बनता है तो अन्तिम प्रतिबिम्ब में मीनार की ऊँचाई क्या है?
हल :

प्रश्न 36.
किसी कैसेग्रेन दूरबीन में चित्र-9.8 में दर्शाए अनुसार दो दर्पणों का प्रयोग किया गया है। इस दूरबीन में दोनों दर्पण एक-दूसरे से 20 मिमी दूर रखे गए हैं। यदि बड़े दर्पण की वक्रता त्रिज्या 220 मिमी हो तथा छोटे दर्पण की वक्रता त्रिज्या 140 मिमी हो तो अनन्त पर रखे किसी बिम्ब का अन्तिम प्रतिबिम्ब कहाँ बनेगा?
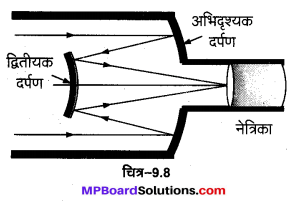
हल :
प्रथम दर्पण हेतु, u =∞ ,f0= – \(\frac{R_{2}}{2}\) = -110 मिमी
अभिदृश्यक
दर्पण सूत्र \(\frac{1}{v}+\frac{1}{\infty}=\frac{1}{-110}\) से \(\frac{1}{v}+\frac{1}{\infty}=\frac{1}{-110}\)
⇒ v = – 110 मिमी
इस दर्पण द्वारा बना प्रतिबिम्ब दर्पण के सामने उससे 110 मिमी दूरी पर बनता है।
∴ दर्पणों के बीच की दूरी = 20 मिमी
∴ इस प्रतिबिम्ब की दूसरे दर्पण से दूरी = 110 – 20 = 90 मिमी
प्रथम दर्पण द्वारा बना प्रतिबिम्ब दूसरे दर्पण के लिए आभासी वस्तु का कार्य करेगा।
∴ दूसरे दर्पण हेतु u = – 90 सेमी*, f’= – \(\frac{R_{2}}{2}\) = – 70 मिमी**
*अभिदृश्यक द्वारा प्रतिबिम्ब उसके सामने 110 सेमी की दूरी पर बनता है अर्थात् यह प्रतिबिम्ब दूसरे दर्पण के बाईं ओर 90 सेमी पर बनता है, अत: u ऋणात्मक लिया गया है।
**ध्यान दें, द्वितीयक दर्पण उत्तल है, जिसका परावर्तक तल दाईं ओर (उल्टा) है, अत: f2 ऋणात्मक लिया गया है।

अत: अन्तिम प्रतिबिम्ब दूसरे दर्पण के पीछे की ओर (वस्तु की ही दिशा में) इस दर्पण से 315 मिमी की दूरी पर बनता है।
प्रश्न 37.
किसी गैल्वेनोमीटर की कुण्डली से जुड़े समतल दर्पण पर लम्बवत् आपतित प्रकाश (चित्र-9.9) दर्पण से टकराकर अपना पथ पुनः अनुरेखित करता है। गैल्वेनोमीटर की कुण्डली में प्रवाहित कोई धारा दर्पण में 3.5° का परिक्षेपण उत्पन्न करती है। दर्पण के सामने 1.5 मीटर की दूरी पर रखे परदे पर प्रकाश के परावर्ती चिह्न में कितना विस्थापन होगा?
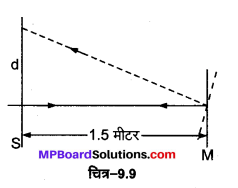
हल :
जब दर्पण में θ = 3.5° का विक्षेप उत्पन्न होता है, तब प्रकाश किरण दोगुने कोण (अर्थात् 20 = 2 × 3.5° = 7°) से घूमती है।
अत: R = 1.5 मीटर दूरी पर रखे परदे पर प्रकाश चिह्न का विस्थापन d = R × 2θ (∵ चाप = कोण x त्रिज्या)
⇒ d = 1.5 × \(\frac{7^{\circ} \times \pi}{180^{\circ}}\) = 0.184 मीटर = 18.4 मीटर।
![]()
प्रश्न 38.
चित्र 9.10 में कोई समोत्तल लेन्स (अपवर्तनांक 1.50) किसी समतल दर्पण के फलक पर किसी द्रव की परत के सम्पर्क में दर्शाया गया है। कोई छोटी सुई जिसकी नोक मुख्य अक्ष पर है, अक्ष के अनुदिश ऊपर-नीचे गति कराकर इस प्रकार समायोजित की जाती है कि सुई की नोक का उल्टा प्रतिबिम्ब सुई की स्थिति पर ही बने। इस स्थिति में सुई की लेन्स से दूरी 45.0 सेमी है। द्रव को हटाकर प्रयोग को दोहराया जाता है। नयी दूरी 30.0 सेमी मापी जाती है। द्रव का अपवर्तनांक क्या है?
हल :
द्रव को हटाकर प्रयोग करते समय –
इस स्थिति में सुई से चलने वाली किरणें काँच के लेन्स से अपवर्तित होकर समतल दर्पण पर अभिलम्बवत् आपतित होती हैं। दर्पण इन किरणों को वापस उन्हीं के मार्ग पर लौटा देता है जिससे किरणें वापस सुई. की स्थिति में ही प्रतिबिम्ब बनाती हैं।
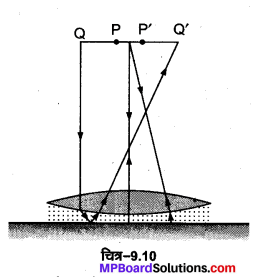
यह स्पष्ट है कि दर्पण की अनुपस्थिति में लेन्स से अपवर्तित किरणें अनन्त पर मिलती हैं। ..
∴ काँच के लेन्स हेतु, u = – 30 सेमी, v = ∞
माना फोकस दूरी = f1

∴ लेन्स की फोकस दूरी f1 = 30 सेमी
यदि इसके प्रत्येक तल की वक्रता त्रिज्या R है, तब
R1 = + R, R2 = – R, n= 1.5

द्रव के साथ प्रयोग करते समय
इस स्थिति में काँच के लेन्स तथा समतल दर्पण के बीच एक द्रव का लेन्स भी बना है। माना इस द्रव लेन्स की फोकस दूरी f2 है, तब

स्पष्ट है कि द्रव लेन्स के प्रथम तल की वक्रता त्रिज्या काँच लेन्स के वक्र तल की वक्रता-त्रिज्या के बराबर है।
∴ द्रव लेन्स हेतु R1= – 30 सेमी, R2 = ∞
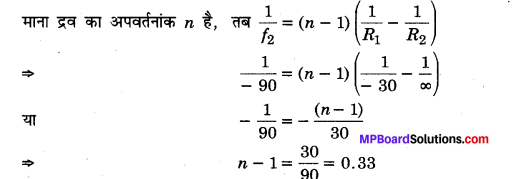
∴ द्रव का अपवर्तनांक n = 1.33
किरण प्रकाशिकी एवं प्रकाशिक यंत्र किरण प्रकाशिकी एवं प्रकाशिक यंत्र NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल
किरण प्रकाशिकी एवं प्रकाशिक यंत्र बहुविकल्पीय प्रश्नोत्तर
प्रश्न 1.
श्वेत प्रकाश का एक लघु स्पन्द वायु से काँच के एक स्लैब पर लम्बवत् आपतित होता है। स्लैब से । गुजरने के पश्चात् सबसे पहले निर्गत होने वाला वर्ण होगा –
(a) नीला
(b) हरा
(c) बैंगनी
(d) लाल।
उत्तर :
(d) लाल।
प्रश्न 2.
एक बिम्ब कि अभिसारी लेन्स के बाईं ओर से 5 मीटर/सेकण्ड की एकसमान चाल से उपगमन करता है और फोकस पर जाकर रुक जाता है। प्रतिबिम्ब –
(a) 5 मीटर/सेकण्ड की एकसमान चाल से लेन्स से दूर गति करता है
(b) एकसमान त्वरण से लेन्स से दूर गति करता है
(c) असमान त्वरण से लेन्स से दूर गति करता है
(d) असमान त्वरण से लेन्स की ओर गति करता है।
उत्तर :
(c) असमान त्वरण से लेन्स से दूर गति करता है
प्रश्न 3.
वायुयान में कोई यात्री –
(a) कभी भी इन्द्रधनुष नहीं देख पाता है
(b) प्राथमिक तथा द्वितीयक इन्द्रधनुष को संकेन्द्री वृत्तों के रूप में देख पाता है
(c) प्राथमिक तथा द्वितीयक इन्द्रधनुष को संकेन्द्री आर्क के रूप में देख पाता है
(d) कभी भी द्वितीयक इन्द्रधनुष नहीं देख पाता है।
उत्तर :
(b) प्राथमिक तथा द्वितीयक इन्द्रधनुष को संकेन्द्री वृत्तों के रूप में देख पाता है
![]()
प्रश्न 4.
आपको प्रकाश के चार स्रोत दिए गए हैं, जिनमें से प्रत्येक से एकल वर्ण-लाल, नीला, हरा तथा पीला प्रकाश मिलता है। मान लीजिए पीले प्रकाश के एक किरण पुंज के लिए दो माध्यमों के अन्तरापृष्ठ पर किसी विशेष आपतन कोण के लिए संगत अपवर्तन कोण 90° है। यदि आपतन कोण को परिवर्तित किए बगैर पीले प्रकाश स्त्रोत को दूसरे प्रकाश स्रोतों से बदल दिया जाए, तो निम्नलिखित कथनों में से कौन-सा कथन सही है?
(a) लाल प्रकाश के किरण पुंज में पूर्ण आन्तरिक परावर्तन होगा
(b) दूसरे माध्यम में अपवर्तित होने पर लाल प्रकाश का किरण पुंज अभिलम्ब की ओर मुड़ जाएगा
(c) नीले प्रकाश के किरण पुंज में पूर्ण आन्तरिक परावर्तन होगा ।
(d) दूसरे माध्यम में अपवर्तित होने पर हरे प्रकाश का किरण पुंज अभिलम्ब से दूर की ओर मुड़ जाएगा।
उत्तर :
(c) नीले प्रकाश के किरण पुंज में पूर्ण आन्तरिक परावर्तन होगा ।
प्रश्न 5.
किसी समतल उत्तल लेन्स के वक्र पृष्ठ की वक्रता त्रिज्या 20 सेमी है। यदि लेन्स के पदार्थ का अपवर्तनांक 1.5 हो, तो यह –
(a) उन बिम्बों के लिए ही उत्तल लेन्स की भाँति कार्य करेगा जो इसके वक्रित भाग की ओर स्थित हैं
(b) वक्रित भाग की ओर स्थित बिम्बों के लिए अवतल लेन्स की भाँति कार्य करेगा
(c) इस बात का ध्यान किए बिना कि बिम्ब इसके किस भाग की ओर स्थित है, उत्तल लेन्स की भाँति कार्य करेगा
(d) इस बात का ध्यान किए बिना कि बिम्ब इसके किस भाग की ओर स्थित है, अवतल लेन्स की भाँति कार्य करेगा।
उत्तर :
(b) वक्रित भाग की ओर स्थित बिम्बों के लिए अवतल लेन्स की भाँति कार्य करेगा
प्रश्न 6.
आयन मण्डल (आयनोस्फियर) द्वारा रेडियो तरंगों के परावर्तन में सम्मिलित परिघटना –
(a) समतल दर्पण द्वारा प्रकाश के परावर्तन के समान है
(b) मरीचिका के समय वायु में होने वाले प्रकाश के पूर्ण आन्तरिक परावर्तन के समान है
(c) इन्द्रधनुष के बनते समय जल के अणुओं द्वारा प्रकाश के परिक्षेपण (वर्ण-विक्षेपण) के समान है
(d) वायु के कणों द्वारा प्रकाश के प्रकीर्णन के समान है।
उत्तर :
(b) मरीचिका के समय वायु में होने वाले प्रकाश के पूर्ण आन्तरिक परावर्तन के समान है
प्रश्न 7.
किसी अवतल दर्पण पर आपतित प्रकाश किरण की दिशा PQ द्वारा दर्शाई गई है जबकि परावर्तन के पश्चात् जिन दिशाओं में यह किरण गमन कर 2-4 सकती है वह 1, 2, 3 तथा 4 द्वारा चिह्नित चार किरणों (चित्र 9.11) द्वारा दर्शायी गई है। चारों किरणों में से कौन-सी किरण परावर्तित किरण की दिशा को सही दर्शाती है?
(a) 1
(b) 2
(c) 3
(d) 4
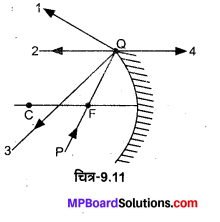
उत्तर :
(b) 2
किरण प्रकाशिकी एवं प्रकाशिक यंत्र अति लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
क्या किसी लेन्स की लाल प्रकाश के लिए फोकस दूरी नीले प्रकाश के लिए उसकी फोकस दूरी से अधिक होगी, समान होगी या कम होगी?
उत्तर :
लेन्स की फोकस दूरी, \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
परन्तु nB > nR, अत: fR > fB
अतः लेन्स की लाल प्रकाश के लिए फोकस दूरी, नीले प्रकाश के लिए उसकी फोकस दूरी से अधिक होगी।
प्रश्न 2.
एक असममित पतला उभयोत्तल लेन्स किसी बिन्दु बिम्ब का प्रतिबिम्ब अपने अक्ष पर बनाता है। यदि लेन्स का पार्श्व परिवर्तन कर रखा जाए तो क्या प्रतिबिम्ब की स्थिति में परिवर्तन होगा?
उत्तर :
नहीं, प्रकाश की उत्क्रमणीयता के कारण लेन्स का पार्श्व परिवर्तन (उल्टा करने) कर रखने पर प्रतिबिम्ब की स्थिति में परिवर्तन नहीं होगा।
![]()
प्रश्न 3.
d1 > d2 > d3 घनत्वों तथा μ1 >μ2 > μ3अपवर्तनांकों के तीन अमिश्रणीय द्रवों को एक बीकर में रखा गया है। प्रत्येक द्रव के स्तम्भ की ऊँचाई । है। बीकर की पैंदी पर एक बिन्दु बनाया गया है। सामान्य निकट-दृष्टि के लिए बिन्दु की आभासी गहराई ज्ञात कीजिए।
उत्तर :
माना μ2अपवर्तनांक के द्रव से देखने पर बिन्दु O की आभासी स्थिति
O1 तथा आभासी गहराई h1 है।

माना μ3 अपवर्तनांक के द्रव से देखने पर बिन्दु O की आभासी स्थिति O2 तथा आभासी गहराई h2 है। अतः
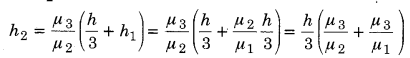
माना वायु से देखने पर बिन्दु O की आभासी स्थिति O3 तथा आभासी गहराई h’ है।

किरण प्रकाशिकी एवं प्रकाशिक यंत्र विस्तृत उत्तरीय प्रश्नोत्तर
प्रश्न 1.
h ऊँचाई के एक जार को μ अपवर्तनांक के एक पारदर्शी द्रव से भरा गया है (चित्र 9.13 )। जार के केन्द्र में इसकी पैंदी पर एक बिन्दु बनाया गया है। उस डिस्क का न्यूनतम व्यास ज्ञात कीजिए जिसे जार के केन्द्र के इधर-उधर शीर्ष पृष्ठ पर सममिततः रखने पर बिन्दु अदृश्य हो जाए।
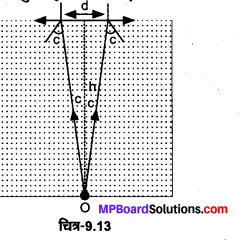
उत्तर :
माना उस डिस्क का व्यास d है जिसे जार के केन्द्र के इधर-उधर शीर्ष पृष्ठ पर देखा जा सकता है। यह तभी सम्भव है जब प्रकाश किरण जल-वायु पृष्ठ पर क्रान्तिक कोण c पर आपतित हो।
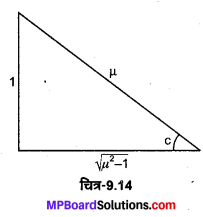
अतः sin c = \(\frac{1}{\mu}\)
जहाँ μ द्रव का अपवर्तनांक है।
चित्र से, \(\tan c=\frac{d / 2}{h}\) या \(\frac{d}{2}\) = h tan c = \(h\frac{1}{\sqrt{\left(\mu^{2}-1\right)}}\)
या \(d=\frac{2 h}{\sqrt{\left(\mu^{2}-1\right)}}\)
![]()
किरण प्रकाशिकी एवं प्रकाशिक यंत्र आंकिक प्रश्नोत्तर
प्रश्न 1.
किसी काँच के प्रिज्म (u = √3) के लिए न्यूनतम विचलन कोण प्रिज्म कोण के बराबर है। प्रिज्म कोण का मान ज्ञात कीजिए।
हल :
दिया है,
u = √3 तथा δm = A
