MP Board Class 12th Physics Important Questions Chapter 9(E) प्रकाशिक यंत्र

Students get through the MP Board Class 12th Physics Important Questions Chapter 9(E) प्रकाशिक यंत्र which are most likely to be asked in the exam.

MP Board Class 12th Physics Important Questions Chapter 9(E) प्रकाशिक यंत्र

अति लघु उत्तरीय प्रश्न 

प्रश्न 1.
सूक्ष्मदर्शी का नाम बताओ जो रीडिंग लेंस के रूप में उपयोगी है।
उत्तर:
सरल सूक्ष्मदर्शी।

प्रश्न 2.
सूक्ष्मदर्शी की विभेदन क्षमता प्रकाश की तरंगदैर्ध्य पर किसी प्रकार निर्भर करती है ?
उत्तर:
प्रकाश की तरंगदैर्घ्य का मान कम होने पर सूक्ष्मदर्शी की विभेदन क्षमता बढ़ जाती है।

प्रश्न 3.
खगोलीय दूरदर्शी की आवर्धन क्षमता का सूत्र लिखिए।
उत्तर:
खगोलीय सूक्ष्मदर्शी की आवर्धन क्षमता m = \(-\frac{f_{o}}{f_{e}}\) होती है।

प्रश्न 4.
सामान्य संयोजन की स्थिति में गैलिलियो दूरदर्शी की लंबाई कितनी होती है ?
उत्तर:
f_o – f_e.

प्रश्न 5.
अपवर्तक तथा परावर्तक दूरदर्शी में से कौन-से दूरदर्शी की लम्बाई अधिक होती है ?
उत्तर:
अपवर्तक दूरदर्शी की लंबाई परावर्तक दूरदर्शी की अपेक्षा अधिक होती है।

प्रश्न 6.
सरल सूक्ष्मदर्शी पर आपतित प्रकाश का रंग उसकी आवर्धन क्षमता को किस प्रकार प्रभावित करता है ?
उत्तर:
बैंगनी रंग के लिए फोकस दूरी कम होती है, अतः आवर्धन क्षमता अधिक होगी। लाल रंग के लिए फोकस दूरी अधिक होते है, अत: आवर्धन क्षमता कम होगी
∵ (m = 1 + \(\frac{\mathrm{D}}{f}\))।

प्रश्न 7.
सरल सूक्ष्मदर्शी में प्रतिबिम्ब कैसा बनता है ?
उत्तर:
सीधा, वस्तु से बड़ा और आभासी।

प्रश्न 8.
संयुक्त सूक्ष्मदर्शी में अन्तिम प्रतिबिम्ब कैसा बनता है ?
उत्तर:
वस्तु से बड़ा, उल्टा और आभासी।

प्रश्न 9.
यदि नेत्रिका की फोकस दूरी कम कर दी जाये तो सूक्ष्मदर्शी को आवर्धन क्षमता पर क्या प्रभाव पड़ेगा?
उत्तर:
आवर्धन क्षमता बढ़ जायेगी।

प्रश्न 10.
अभिदृश्यक की फोकस दूरी बढ़ा देने पर सूक्ष्मदर्शी तथा दूरदर्शी की आवर्धन क्षमता पर क्या प्रभाव पड़ेगा?
उत्तर:
सूक्ष्मदर्शी की आवर्धन क्षमता कम हो जायेगी जबाके दूरदर्शी की आवर्धन क्षमता बढ़ जायेगी।

प्रश्न 11.
दूरदर्शी द्वारा प्रतिबिम्ब वस्तु से छोटा बनता है फिर दूरदर्शी के क्या लाभ हैं ?
उत्तर:
प्रतिबिम्ब नेत्र के पास बनता है जिससे प्रतिबिम्ब द्वारा नेत्र पर अंतरित कोण बढ़ जाता है।

प्रश्न 12.
संयुक्त सूक्ष्मदर्शी में अभिदृश्यक और नेत्रिका दोनों की फोकस दूरियाँ कम होती है, क्यों?
उत्तर:
अभिदृश्यक और नेत्रिका की फोकस दूरियाँ कम होने से संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता अधिक होती है।

प्रश्न 13.
सामान्य समायोजन का क्या अर्थ है ?
उत्तर:
सामान्य समायोजन की स्थिति में सूक्ष्मदर्शी या दूरदर्शक में अंतिम प्रतिबिम्ब अनंत पर बनता है। इस स्थिति में नेत्र श्रांत अवस्था में होता है उस पर कोई तनाव नहीं रहता है।

प्रश्न 14.
सूक्ष्मदर्शी और दूरदर्शी का मूल कार्य क्या है ?
उत्तर:
दोनों का मूल कार्य दर्शन कोण के मान को बढ़ाना है जिससे वस्तु आवर्धित रूप में दिखाई दे।

लघु उत्तरीय प्रश्न

प्रश्न 1.
खगोलीय दूरदर्शी की आवर्धन क्षमता किस प्रकार बढ़ाई जा सकती है ?
उत्तर:
खगोलीय दूरदर्शी की आवर्धन क्षमता m = \(\frac{f_{o}}{f_{e}}\)
इस सूत्र से स्पष्ट है कि आवर्धन क्षमता m के मान को अधिक होने के लिए-
(i) अभिदृश्यक की फोकस दूरी f_o को अधिक-से-अधिक तथा
(ii) नेत्रिका की फोकस दूरी f_e को एक से कम होना चाहिए।

प्रश्न 2.
दूरदर्शी को उलटने पर प्रतिबिम्ब काफी छोटा हो जाता है, परन्तु सूक्ष्मदर्शी में ऐसा नहीं होता है, क्यों?
उत्तर:
दूरदर्शी की आवर्धन क्षमता m = \(\frac{f_{o}}{f_{e}}\) है। यदि दूरदर्शी को उलट दिया जाये तो आवर्धन
क्षमता \(\frac{f_{o}}{f_{e}}\) होती है। चूँकि f_e << f_o, अत: प्रतिबिम्ब छोटा बनता है।
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता m = \(-\frac{v_{o}}{u_{o}} \cdot \frac{\mathrm{D}}{f_{e}}\) होती है। u_o का मान f_o से कुछ ही अधिक होता
है। अतः आवर्धन क्षमता को m = \(-\frac{v_{o}}{u_{o}} \cdot \frac{\mathrm{D}}{f_{e}}\) भी लिखा जा सकता है। सूक्ष्मदर्शी को उलटकर देखने में v_o के मान में कोई परिवर्तन नहीं होगा, जिससे उसकी आवर्धन क्षमता उतनी ही बनी रहेगी।

प्रश्न 3.
दूरदर्शी के अभिदृश्यक का व्यास बढ़ाने पर निम्न पर क्या प्रभाव पड़ेगा-
(i) आवर्धन क्षमता,
(ii) विभेदन क्षमता।
उत्तर:
(i) अपरिवर्तित रहेगी,
(ii) बढ़ जायेगी, क्योंकि विभेदन क्षमता = \(\frac{a}{1 \cdot 22 \lambda}\) जहाँ a अभिदृश्यक का व्यास हैं।

प्रश्न 4.
चन्द्रमा की अपेक्षा सूर्य का व्यास कई सौ गुना बड़ा है। पूर्ण सूर्यग्रहण के समय चन्द्रमा से सूर्य पूरा ढंक जाता है, क्यों ?
उत्तर–पूर्ण सूर्यग्रहण के समय चन्द्रमा, सूर्य और पृथ्वी के बीच में होता है। इस स्थिति में सूर्य और चन्द्रमा द्वारा बनाये गये दृष्टिकोण बराबर होते हैं । अतः पूर्ण सूर्यग्रहण के समय चन्द्रमा से सूर्य पूरा ढंक जाता है।

प्रश्न 5.
संयुक्त सूक्ष्मदर्शी में अभिदृश्यक की फोकस दूरी कम क्यों होनी चाहिए?

अथवा

संयुक्त सूक्ष्मदर्शी के अभिदृश्यक की फोकस दूरी कम तथा आवर्धन-क्षमता ऋणात्मक होती है, क्यों?
उत्तर:
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता m = \(\frac{v_{o}}{u_{o}}-\left(1+\frac{\mathrm{D}}{f_{e}}\right)\)

उपर्युक्त सूत्र से स्पष्ट है कि m के मान को अधिक होने के लिए , का मान कम होना चाहिए अर्थात् वस्तु को अभिदृश्यक के निकट होना चाहिए, किन्तु वस्तु को सदैव अभिदृश्यक के फोकस के बाहर रखा जाता है। अतः अभिदृश्यक की फोकस दूरी कम होनी चाहिए।
अन्तिम प्रतिबिम्ब वस्तु के सापेक्ष उल्टा बनता है। अतः आवर्धन-क्षमता ऋणात्मक होती है।

प्रश्न 6.
दूरदर्शी की विभेदन क्षमता से आप क्या समझते हैं ? इसका सूत्र लिखिए।
उत्तर:
दो दूरस्थ वस्तुओं के, जो दूरदर्शी की सहायता से अलग-अलग देखी जा सकती हैं, न्यूनतम कोणीय हटाव के व्युत्क्रम को दूरदर्शी की विभेदन क्षमता कहते हैं।
दूरदर्शी की विभेदन क्षमता = \(\frac{a}{1 \cdot 22 \lambda}\)
जहाँ, λ प्रकाश का तरंगदैर्घ्य तथा a अभिदृश्यक का व्यास है।

प्रश्न 7.
सूक्ष्मदर्शी की विभेदन क्षमता से आप क्या समझते हैं ? इसका सूत्र लिखिए।
उत्तर:
सूक्ष्मदर्शी की विभेदन क्षमता का निर्धारण दो बिन्दुओं के बीच की उस न्यूनतम दूरी से किया जाता है, जिससे वे वस्तुएँ सूक्ष्मदर्शी से देखे जाने पर अलग-अलग दिखाई दे सकें।
सूक्ष्मदर्शी की विभेदन क्षमता = \(\frac{2 \mu \cdot \sin \theta}{\lambda}\)
जहाँ, λ प्रकाश का तरंगदैर्घ्य, μ वस्तु और अभिदृश्यक के बीच का माध्यम तथा θ वस्तु के प्रकाश से शंकु का अर्द्धकोण है।

प्रश्न 8.
आकाशीय दूरदर्शी किसे कहते हैं ?
उत्तर:
जिस दूरदर्शी का उपयोग आकाशीय पिण्डों को देखने में किया जाता है उसे आकाशीय (खगोलीय) दूरदर्शी कहा जाता है।

प्रश्न 9.
क्या यह सम्भव है कि सूक्ष्मदर्शी नलिका को उलट देने से दूरदर्शी नलिका बन जाये ? अपने उत्तर का कारण स्पष्ट कीजिए।
उत्तर:
सूक्ष्मदर्शी नलिका को उलट देने से दूरदर्शी नलिका बन जाये, यह सम्भव नहीं है, क्योंकि सूक्ष्मदर्शी के अभिदृश्यक और नेत्रिका की फोकस दूरियों में अन्तर कम होता है, जबकि दूरदर्शी के अभिदृश्यक और नेत्रिका की फोकस दूरियों में अन्तर अधिक होता है।

प्रश्न 10.
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता किस प्रकार बढ़ाई जा सकती है?
उत्तर:

1. अभिदृश्यक की फोकस दूरी कम करके,
2. नेत्रिका की फोकस दूरी कम करके,
3. सूक्ष्मदर्शी की नली की लम्बाई बढ़ाकर।

प्रश्न 11.
(क) सूक्ष्मदर्शी और दूरदर्शी में उच्च आवर्धन क्षमता के साथ-साथ पर्याप्त विभेदनक्षमता भी होनी चाहिये, क्यों?
(ख) फोटोग्राफिक लेंस का द्वारक छोटा होता है जबकि दूरदर्शी के अभिदृश्यक का द्वारक बहुत बड़ा होता है, क्यों?
उत्तर:
(क) आवर्धन क्षमता अधिक होने से वस्तु बड़ी और स्पष्ट दिखायी देती है, किन्तु यदि विभेदन क्षमता कम है तो उसकी संरचना स्पष्ट नहीं होगी।

(ख) फोटोग्राफिक लेंस का द्वारक छोटा होता है। इसका कारण यह है कि द्वारक छोटा होने से फोकस की गहराई बढ़ जाती है।
दूरदर्शी के अभिदृश्यक का द्वारक बड़ा होता है इसके निम्न कारण हैं-

1. द्वारक बड़ा होने से इसकी विभेदन क्षमता बढ़ जाती है।
2. द्वारक बड़ा होने से दूरदर्शी में अधिक प्रकाश प्रवेश करता है, जिससे चमकीला प्रतिबिम्ब बनता है।

प्रश्न 12.
खगोलीय दूरदर्शी तथा गैलीलियो दूरदर्शी में समानताएँ लिखिए।
उत्तर:

खगोलीय दूरदर्शी	गैलीलियो दूरदर्शी
1. यदि अंतिम प्रतिबिम्ब अनंत पर बने तो आवर्धन क्षमता m = \(\frac{f_{o}}{f_{e}}\).	1. इसमें भी अंतिम प्रतिबिम्ब अनंत पर बने तो आवर्धन क्षमता m = \(\frac{f_{o}}{f_{e}}\).
2. अभिदृश्यक का मुख्य व्यास, नेत्रिका के मुख्य व्यास से अधिक होता है।	2. इसमें भी अभिदृश्यक का मुख्य व्यास नेत्रिका के मुख्य व्यास से अधिक होता है।
3. अभिदृश्यक की फोकस दूरी नेत्रिका की फोकस दूरी से अधिक होती है।	3. इसमें भी अभिदृश्यक की फोकस दूरी नेत्रिका की फोकस दूरी से अधिक होती है।

प्रश्न 13.
खगोलीय दूरदर्शी तथा गैलीलियो दूरदर्शी में अंतर (असमानताएँ) लिखिए।
उत्तर:

खगोलीय दूरदर्शी	गैलीलियो दूरदर्शी
1. इस दूरदर्शी की नली की लंबाई अधिक होती है। यदि अंतिम प्रतिबिम्ब अनंत पर बने तो नली की लंबाई f<sub>O</sub> + f<sub>e</sub> होती है।	1. इस दूरदर्शी की लंबाई कम होती है। यदि अंतिम प्रतिबिम्ब अनंत पर बने तो इसकी लंबाई f<sub>O</sub> – f<sub>e</sub> होती है।
2. इसमें उत्तल लेंस नेत्रिका का कार्य करता है।	2. इसमें अवतल लेंस नेत्रिका का कार्य करता है।
3. अंतिम प्रतिबिम्ब वस्तु के सापेक्ष उल्टा बनता है।	3. अंतिम प्रतिबिम्ब वस्तु के सापेक्ष सीधा बनता है।
4. इसमें क्रास तार लगाये जा सकते हैं। अतः इस दूरदर्शी से मापन संभव है।	4. इसमें क्रास तार नहीं लगाये जा सकते हैं, अतः इस दूरदर्शी से मापन संभव नहीं है।
5. इसकी आवर्धन क्षमता अधिक होती है।	5. इसकी आवर्धन क्षमता कम होती है।

प्रश्न 14.
दूरदर्शी की आवर्धन क्षमता एवं विभेदन क्षमता में अन्तर लिखिए।
उत्तर:
दूरदर्शी की आवर्धन क्षमता एवं विभेदन क्षमता में अन्तर-

आवर्धन क्षमता	विभेदन क्षमता
1. अन्तिम प्रतिबिम्ब द्वारा निर्मित दृष्टि-कोण और वस्तु द्वारा निर्मित दृष्टि-कोण के अनुपात को दूरदर्शी की आवर्धन क्षमता कहते हैं।	1. दो दूरस्थ वस्तुओं के, जो दूरदर्शी की सहायता से अलग-अलग देखी जा सकती हैं, न्यूनतम कोणीय हटाव के व्युत्क्रम को दूरदर्शी की विभेदन क्षमता कहते हैं।
2. अधिक आवर्धन क्षमता के लिए अभिदृश्यक की फोकस दूरी अधिक एवं नेत्रिका की फोकस दूरी कम होनी चाहिए।	2. अधिक विभेदन क्षमता के लिए अभिदृश्यक का व्यास अधिक होना चाहिए।

प्रश्न 15.
संयुक्त सूक्ष्मदर्शी और खगोलीय दूरदर्शी में अन्तर लिखिए।
उत्तर:
दूरदर्शी की आवर्धन क्षमता एवं विभेदन क्षमता में अन्तर-

संयुक्त सूक्ष्मदर्शी	खगोलीय दूरदर्शी
1. इसकी सहायता से निकट स्थित सूक्ष्म वस्तुओं को आवर्धित रूप में देखा जाता है।	1. इसकी सहायता से आकाशीय पिण्डों को स्पष्ट देखा जाता है।
2. इसमें अभिदृश्यक की फोकस दूरी नेत्रिका की फोकस दूरी से कम होती है।	2. इसमें अभिदृश्यक की फोकस दूरी नेत्रिका की फोकस दूरी से बहुत अधिक होती है।
3. इसमें अभिदृश्यक और नेत्रिका की फोकस दूरियों में अन्तर कम होता है।	3. इसमें अभिदृश्यक और नेत्रिका की फोकस दूरियों में अन्तर अधिक होता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
सरल सूक्ष्मदर्शी क्या है ? स्वच्छ किरण आरेख खींचकर इसका सिद्धान्त समझाइये। इसके दो उपयोग लिखिए।
उत्तर:

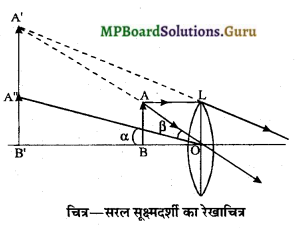
सरल सूक्ष्मदर्शी – यह एक ऐसी युक्ति है जिसकी सहायता से सूक्ष्म वस्तु को आवर्धित रूप में देखा जा सकता है। यह कम फोकस दूरी वाला एक उत्तल लेंस होता है।
किरण आरेख – L = उत्तल लेंस, AB = वस्तु,
A’B’ = आवर्धित प्रतिबिम्ब।
सिद्धान्त – यदि कोई वस्तु उत्तल लेंस के प्रकाश केन्द्र और फोकस के बीच स्थित हो तो लेंस द्वारा उसका प्रतिबिम्ब आभासी, सीधा और आवर्धित बनता है।
उपयोग-
(i) रीडिंग लेंस के रूप में,
(ii) सूक्ष्म वस्तु को आवर्धित रूप में देखने के लिए।

प्रश्न 2.
सूक्ष्मदर्शी की विभेदन क्षमता का वर्णन निम्नलिखित शीर्षकों में कीजिये।
(a) किरण आरेख,
(b) विभेदन क्षमता हेतु सूत्र का निगमन।
(c) विभेदन क्षमता कैसे बढ़ायी जा सकती है ?
उत्तर:

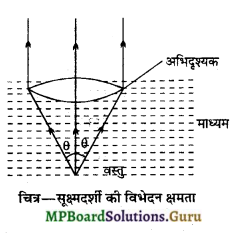
(a) किरण आरेख – संलग्न चित्र देखें।
(b) विभेदन क्षमता हेतु सूत्र का निगमन – सूक्ष्मदर्शी की विभेदन क्षमता का निर्धारण दो बिन्दुओं के बीच की उस न्यूनतम दूरी से किया जाता है, जिससे वे वस्तुएँ सूक्ष्मदर्शी से देखे जाने पर अलग-अलग दिखायी दे सकें।

एबी (abbe) के अनुसार सूक्ष्मदर्शी द्वारा विभेदित की जा सकने वाली दो बिन्दुओं के बीच की न्यूनतम दूरी निम्न समीकरण द्वारा दी जा सकती है-
d = \(\frac{\lambda}{2 \mu \sin \theta}\) …………(1)
जहाँ λ वस्तु को प्रकाशित करने के लिये प्रयुक्त प्रकाश का तरंगदैर्घ्य है । θ वस्तु के प्रकाश से शंकु का अर्द्धकोण है तथा । वस्तु व अभिदृश्यक के बीच के माध्यम का अपवर्तनांक है।
समी. (1) से,
सूक्ष्मदर्शी की विभेदन क्षमता = \(\frac{2 \mu \sin \theta}{\lambda}\)
राशि 2µsinθ को सूक्ष्मदर्शी का आंकिक द्वारक कहते हैं। नेत्र के लिये 2µsinθ = 0.004 होता है।
उपर्युक्त सूत्र से स्पष्ट है कि सूक्ष्मदर्शी की विभेदन क्षमता अधिक होगी, यदि-
(i) λ का मान कम हो।
(ii) आंकिक द्वारक 2µsinθ का मान अधिक हो।
(iii) सूक्ष्मदर्शी की विभेदन क्षमता को बढ़ाने के लिये विशेष प्रकार का अभिदृश्यक जिसे तेल निमज्जन अभिदृश्यक कहते हैं, प्रयुक्त किया जाता है। इस प्रकार के सूक्ष्मदर्शी से देखी जाने वाली वस्तु को वायु में रखने के बजाय अधिक अपवर्तनांक वाले द्रव में रखा जाता है।

प्रश्न 3.
संयुक्त सूक्ष्मदर्शी का नामांकित रेखाचित्र खींचिये तथा इसकी कार्यविधि बताइये।
उत्तर:
नामांकित रेखाचित्र-

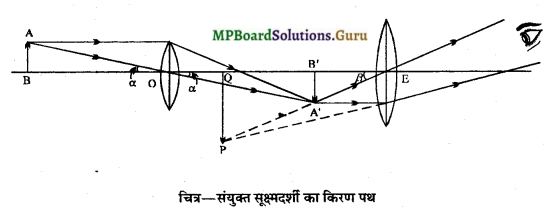
जहाँ O = अभिदृश्यक, E = नेत्रिका, AB = वस्तु, PQ = प्रतिबिम्ब ।

कार्य-विधि – जिस वस्तु AB को देखना होता है उसे अभिदृश्यक O के फोकस से कुछ बाहर रखते हैं। अभिदृश्यक O द्वारा वस्तु AB का उल्टा, वास्तविक और आवर्धित प्रतिबिम्ब A’B’ बनता है । नेत्रिका E की दूरी इस प्रकार समंजित करते हैं कि वह प्रतिबिम्ब उसके फोकस व प्रकाश केन्द्र के बीच बने। A’B’ नेत्रिका E के लिए वस्तु का कार्य करता है, जिसका अन्तिम प्रतिबिम्ब PQ नेत्रिका से स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है। यह प्रतिबिम्ब प्राप्त करने के लिए वस्तु या ग्लाइड को प्राय: उल्टा रखते हैं।
यदि प्रतिबिम्ब A’B’ नेत्रिका E के फ़ोकस पर बने तो अन्तिम प्रतिबिम्ब नेत्रिका से अनन्त दूरी पर बनता है।

प्रश्न 4.
खगोलीय दूरदर्शी का नामांकित रेखाचित्र बनाकर उसकी कार्य-विधि लिखिए।
उत्तर:

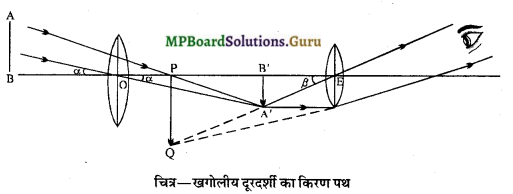
जहाँ O = अभिदृश्यक, E= नेत्रिका, AB = वस्तु, PQ = प्रतिबिम्ब ।

कार्य-विधि-दूर (अनन्त) पर स्थित वस्तु से आने वाली समान्तर किरणें अभिदृश्यक O से अपवर्तन के पश्चात् उसके फोकस तल पर मिलती हैं। अत: फोकस तल पर वस्तु का वास्तविक और उल्टा प्रतिबिम्ब A ‘B’ पर बनता है। नेत्रिका E की दूरी इस प्रकार समंजित की जाती है कि प्रतिबिम्ब A’B’ उसके फोकस और प्रकाश केन्द्र के बीच बने । प्रतिबिम्ब A’B’ नेत्रिका के लिए वस्तु का कार्य करता है। अतः अन्तिम प्रतिबिम्ब PQ स्पष्ट दूरी की न्यूनतम दूरी पर बनता है। यह प्रतिबिम्ब आभासी तथा वस्तु के सापेक्ष उल्टा होता है।

प्रश्न 5.
किसी प्रकाशिक यन्त्र की विभेदन क्षमता से क्या तात्पर्य है ?
(i) सूक्ष्मदर्शी और
(ii) दूरदर्शी की विभेदन क्षमता के सूत्र लिखिए तथा बताइए कि इसे कैसे बढ़ाया जा सकता है ?
उत्तर:
विभेदन क्षमता – किसी प्रकाशिक यन्त्र द्वारा दो समीपवर्ती वस्तुओं के प्रतिबिम्बों को अलगअलग करने की क्षमता को उसकी विभेदन क्षमता कहते हैं।
(i) सूक्ष्मदर्शी की विभेदन क्षमता = \(\frac{2 \mu \sin \theta}{\lambda}\)
जहाँ μ वस्तु और अभिदृश्यक के बीच के माध्यम का अपवर्तनांक, θ वस्तु के प्रकाश से शंकु का अर्द्धकोण तथा λ प्रकाश का तरंगदैर्घ्य है। अतः सूक्ष्मदर्शी की विभेदन क्षमता अधिक होगी यदि-
(क) λ का मान कम हो अर्थात् वस्तु को प्रकाशित करने के लिए प्रयुक्त प्रकाश का तरंगदैर्घ्य कम होना चाहिए।
(ख) μ का मान अधिक हो अर्थात् वस्तु को अधिक अपवर्तनांक वाले माध्यम में रखा जाना चाहिए।
(ग) अर्द्धकोण θ का मान अधिक होना चाहिए।
(ii) दूरदर्शी की विभेदन क्षमता = \(\frac{a}{1 \cdot 22 \lambda}\)

प्रश्न 6.
सरल सूक्ष्मदर्शी का वर्णन निम्नलिखित शीर्षकों के अन्तर्गत कीजिए-
(i) प्रतिबिम्ब बनने का रेखाचित्र,
(ii) आवर्धन क्षमता के लिए व्यंजक जबकि अंतिम प्रतिबिम्ब
(a) स्पष्ट दृष्टि की न्यूनतम दूरी पर बने, (b) अनन्त पर बने।

अथवा

(a) नामांकित रेखाचित्र,
(b) आवर्धन क्षमता के लिए सूत्र की व्युत्पत्ति (D) दूरी के लिए।

अथवा

सरल सूक्ष्मदर्शी का नामांकित चित्र खींचकर उसकी आवर्धन क्षमता के लिए सूत्र की स्थापना कीजिए।
उत्तर:
(i) प्रतिबिम्ब बनने का रेखाचित्र – दीर्घ उत्तरीय प्रश्न क्रमांक 1 देखिए।

(ii) आवर्धन क्षमता – प्रतिबिम्ब द्वारा निर्मित दर्शन कोण और स्पष्ट दृष्टि की न्यूनतम दूरी पर स्थित वस्तु द्वारा निर्मित दर्शन कोण के अनुपात को सरल सूक्ष्मदर्शी की आवर्धन क्षमता कहते हैं।
सूत्र के रूप में,

या m = \(\frac{\beta}{\alpha}\)
चूँकि α और β के मान अत्यन्त कम होते हैं। अत: α = tan α तथा β = tanβ ले सकते हैं।

चिन्ह परिपाटी के अनुसार D ऋणात्मक होगा तथा OB = -u.
∴ m = \(\frac{-D}{-u}\)
या m = \(\frac{\mathrm{D}}{u}\) …………..(2)

(a) जब प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने – इस स्थिति में
v = -D
चित्र परिपाटी से u ऋणात्मक तथा f धनात्मक होगा।
लेंस के सामान्य सूत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) से’
\(\frac{1}{f}=\frac{1}{-D}-\frac{1}{-u}\)
या \(\frac{1}{f}=\frac{-1}{D}+\frac{1}{u}\)
या \(\frac{\mathrm{D}}{f}=-1+\frac{\mathrm{D}}{u}\)
या \(1+\frac{D}{f}=\frac{D}{u}\)
समी. (2) में मान रखने पर,
m = 1 + \(\frac{\mathrm{D}}{f}\) …………..(3)

(b) जब प्रतिबिम्ब अनन्त पर बने-
इस स्थिति में u = f
समी. (2) में मान रखने पर,
m = \(\frac{\mathrm{D}}{f}\) ……………..(4)

प्रश्न 7.
संयुक्त सूक्ष्मदर्शी का वर्णन निम्न शीर्षकों के अंतर्गत कीजिए-
(i) प्रतिबिम्ब बनने की व्यवस्था का किरण पथ सहित चित्र।
(ii) आवर्धन क्षमता के सूत्र की स्थापना जबकि प्रतिबिम्ब-
(a) स्पष्ट दृष्टि की न्यूनतम दूरी पर बने,
(b) अनन्त पर बने।

अथवा

(i) प्रतिबिम्ब बनने के किरण पथ का नामांकित चित्र।
(ii) अधिक आवर्धन क्षमता के लिए आवश्यक प्रतिबंध।
उत्तर:
संयुक्त सूक्ष्मदर्शी – आवर्धन-क्षमता बढ़ाने के लिए दो अलग-अलग लेंसों से बने सूक्ष्मदर्शी का उपयोग करते हैं, जिसे संयुक्त सूक्ष्मदर्शी कहते हैं।
(i) नामांकित रेखाचित्र या किरण पथ-

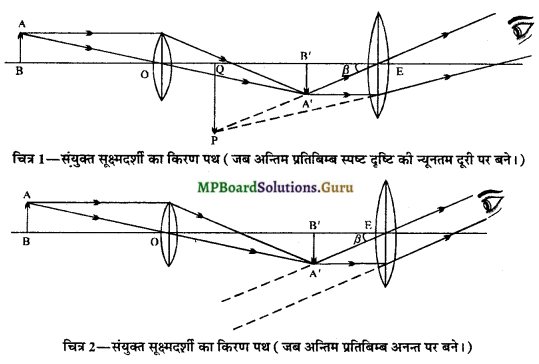
(ii) आवर्धन-क्षमता की गणना-प्रतिबिम्ब द्वारा निर्मित दृष्टि कोण और स्पष्ट दृष्टि की न्यूनतम दूरी पर बने कोण के अनुपात को संयुक्त सूक्ष्मदर्शी की आवर्धन-क्षमता कहते हैं। इसे m से प्रदर्शित करते है।
सूत्र के रूप में,


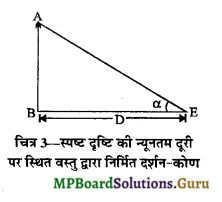
यदि अंतिम प्रतिबिम्ब द्वारा निर्मित दर्शन कोण (दृष्टि कोण) β तथा स्पष्ट दृष्टि की न्यूनतम दूरी पर बना कोण α हो, तो आवर्धन क्षमता
m = \(\frac{\beta}{\alpha}\)
∵ α और β के मान अत्यन्त कम होते हैं, अतः
α = tanα तथा β = tanβ
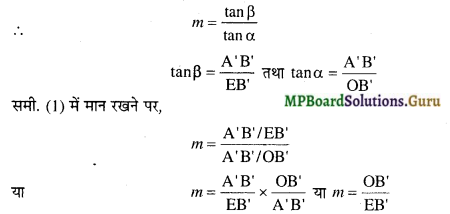
m = \(\frac{\tan \beta}{\tan \alpha}\) ………(1)
अब चित्र 3 से,
tanα = \(\frac{\mathrm{AB}}{\mathrm{D}}\)
चित्र 1 या चित्र 2 से,
tanβ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{EB}^{\prime}}\)
समी. (1) में मान रखने पर,
m = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime} / \mathrm{EB}^{\prime}}{\mathrm{AB} / \mathrm{D}}\)
या m = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}} \times \frac{\mathrm{D}}{\mathrm{EB}^{\prime}}\) ………….(2)
अब चित्रानुसार ΔA’OB’ तथा ΔAOB समरूप हैं, अतः
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{OB}^{\prime}}{\mathrm{OB}}\)
समी. (2) में मान रखने पर,
m = \(\frac{\mathrm{OB}^{\prime}}{\mathrm{OB}} \times \frac{\mathrm{D}}{\mathrm{EB}^{\prime}}\) ……………..(3)
चिन्ह परिपाटी से,
OB = अभिदृश्यक से वस्तु की दूरी = -u_o
OB’ = अभिदृश्यक से प्रतिबिम्ब A’B’ की दूरी = v_o
EB’ = नेत्रिका से वस्तु की दूरी = -u_e
D = स्पष्ट दृष्टि की न्यूनतम दूरी = -D
समी. (3) में मान रखने पर,
m = \(\frac{v_{o}}{-u_{o}} \times \frac{-\mathrm{D}}{-u_{e}}\) या m = \(-\frac{v_{o}}{u_{o}} \times\left(\frac{\mathrm{D}}{u_{e}}\right)\) …………..(4)

I. जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने-मानलो नेत्रिका की फोकस – दूरी f_e है, तब u = -u_e तथा v = -D
अतः लेंस के सामान्य सूत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) से,
या \(\frac{1}{f_{e}}=\frac{1}{-\mathrm{D}}-\frac{1}{-u_{e}}\)
या \(\frac{1}{f_{e}}=-\frac{1}{\mathrm{D}}+\frac{1}{u_{e}}\)
दोनों पक्षों में D का गुणा करने पर,

इस स्थिति में सूक्ष्मदर्शी की नली की लम्बाई = v_o + u_e.

II. जब अन्तिम प्रतिबिम्ब अनन्त पर बने – यदि प्रतिबिम्ब A’B’ नेत्रिका E के फोकस पर बनता है, तो अन्तिम प्रतिबिम्ब अनन्त पर बनेगा। इस स्थिति में u_e = f_e
समीकरण (4) में मान रखने पर,
m = \(\frac{-v_{o}}{u_{o}} \cdot \frac{\mathrm{D}}{f_{e}}\) ………….(6)
इस स्थिति में सूक्ष्मदर्शी की नली की लम्बाई = v_o + f_e.

अधिक आवर्धन-क्षमता के लिए शर्ते-
(1) u_o का मान कम होना चाहिए अर्थात् वस्तु को अभिदृश्यक के नजदीक रखना चाहिए किन्तु वस्तु को अभिदृश्यक के फोकस के बाहर रखा जाता है। अतः अभिदृश्यक की फोकस-दूरी कम होनी चाहिए।
(2) f_e का मान कम होना चाहिए अर्थात् नेत्रिका की फोकस-दूरी कम होनी चाहिए।
(3) v_o का मान अधिक होना चाहिए। इसके लिए वस्तु AB को अभिदृश्यक लेंस O के फोकस के समीप रखना चाहिए। चूँकि अभिदृश्यक द्वारा वस्तु का बना प्रतिबिम्ब वास्तविक होता है। v_o का मान अधिक होने का अर्थ है कि सूक्ष्मदर्शी नली की लम्बाई अधिक होनी चाहिए।

प्रश्न 8.
खगोलीय (आकाशीय) दूरदशी का वर्णन निम्न बिन्दुओं के आधार पर कीजिए-
(1) प्रतिबिम्ब बनने की व्यवस्था का किरण पथ सहित चित्र।
(2) आवर्धन क्षमता के लिए सूत्र की स्थापना जबकि-
(a) प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने।
(b) अनंत पर बने।
उत्तर:
(1) प्रतिबिम्ब बनने की व्यवस्था का किरण पथ सहित चित्र-


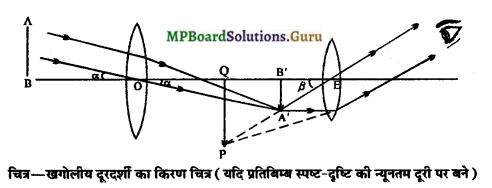
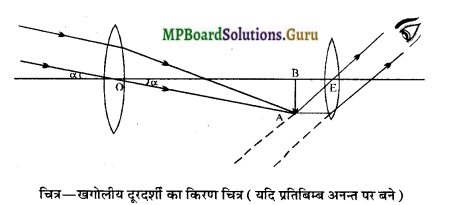
0 → अभिदृश्यक, E → नेत्रिका, AB → वस्तु तथा PQ → अंतिम प्रतिबिम्ब।

(2) आवर्धन क्षमता के लिए सूत्र की स्थापना-
आवर्धन-क्षमता-अन्तिम प्रतिबिम्ब द्वारा निर्मित दर्शन-कोण और वस्तु द्वारा निर्मित दर्शन-कोण के अनुपात को खगोलीय दूरदर्शी की आवर्धन-क्षमता कहते हैं। चूँकि वस्तु अनन्त पर है, अतः वस्तु द्वारा अभिदृश्यक पर बनाये गये कोण को वस्तु द्वारा आँख पर बनाये गये कोण (दर्शन-कोण) के बराबर माना जा सकता है।

या m = \(\frac{\beta}{\alpha}\)
चूँकि α और β के मान बहुत ही कम होते हैं, अत: α = tanα तथा β = tanβ लिखा जा सकता है।

परन्तु OB’ = f_o = अभिदृश्यक की फोकस-दूरी
EB’= -u_e = नेत्रिका से प्रतिबिम्ब A’B’ की दूरी।
∴ m = \(\frac{f_{o}}{-u_{e}}\) या m = \(-\frac{f_{0}}{u_{e}}\) ………..(2)

स्थिति I. जब अंतिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने – मानलो नेत्रिका की फोकसदूरी f_e है। तब नेत्रिका के लिए u = -u_e तथा v = – D.
अतः लेंस के सामान्य सत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
या \(\frac{1}{f_{e}}=\frac{1}{-D}-\frac{1}{-u_{e}}\)

इस स्थिति में दूरदर्शी की नली की लम्बाई = f_O + u_e.

II. जब अंतिम प्रतिबिम्ब अनन्त पर बने-यदि अभिदृश्यक द्वारा वस्तु का प्रतिबिम्ब A’B’ नेत्रिका के फोकस पर बने तो नेत्रिका द्वारा अंतिम प्रतिबिम्ब अनन्त पर बनेगा। इस स्थिति में,
u_e = f_e
समी. (2) में मान रखने पर,
m = \(\frac{-f_{o}}{f_{e}}\) ………..(4)
इस स्थिति में दूरदर्शी की नली की लम्बाई = f_o + f_e

प्रश्न 9.
पार्थिव दूरदर्शी का वर्णन निम्न बिन्दुओं के आधार पर कीजिए-
(1) प्रतिबिम्ब का रेखाचित्र।।
(2) आवर्धन क्षमता की गणना जबकि अंतिम प्रतिबिम्ब-
(a) स्पष्ट दृष्टि की न्यूनतम दूरी पर बने।
(b) अनंत पर बने।
उत्तर:
(1) प्रतिबिम्ब का रेखाचित्र

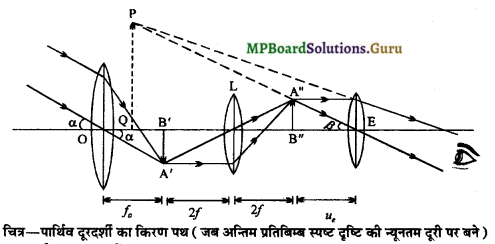
(2) आवर्धन क्षमता की गणना-
आवर्धन-क्षमता-अंतिम प्रतिबिम्ब द्वारा निर्मित दर्शन-कोण और वस्तु द्वारा निर्मित दर्शन-कोण के अनुपात को पार्थिव दूरदर्शी की आवर्धन-क्षमता कहते हैं।

या m = \(\frac{\beta}{\alpha}\)

वस्तु अत्यधिक दूरी पर होती है। अत: वस्तु द्वारा अभिदृश्यक पर बनाये गये कोण को वस्तु द्वारा आँख पर बनाये गये कोण (दर्शन-कोण) के बराबर माना जा सकता है।
α और β के मान बहुत कम होते हैं । अत: α = tanα तथा β = tanβ ले सकते हैं।


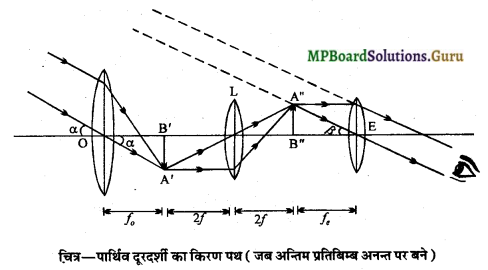
या m = \(\frac{-\mathrm{OB}^{\prime}}{\mathrm{EB}^{\prime \prime}}\) ………..(2)
∵ OB’ = अभिदृश्यक की फोकस दूरी = f_o
EB” = नेत्रिका से वस्तु की दूरी = -u_e
समी. (2) में मान रखने पर,
m = \(\frac{-f_{o}}{-u_{e}}\)
या m = \(\frac{f_{o}}{u_{e}}\) …………(3)

स्थिति (a) जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने – मानलो नेत्रिका की फोकसदूरी है। तब नेत्रिका के लिए u = -u_e तथा v = -D
अतः लेंस के सामान्य सूत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) से, \(\frac{1}{f_{e}}=\frac{1}{-\mathrm{D}}-\frac{1}{-u_{e}}\)

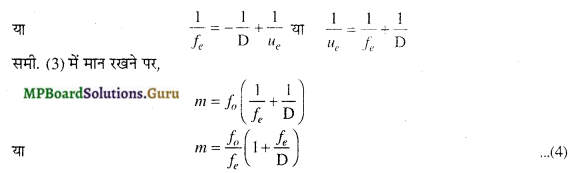
इस स्थिति में दूरदर्शी की नली की लम्बाई = f_o + 4f + u_e.

(b) जब अन्तिम प्रतिबिम्ब अनन्त पर बने-जब प्रतिलोमक लेंस द्वारा बना प्रतिबिम्ब A”B” नेत्रिका के फोकस पर होता है, तो अन्तिम प्रतिबिम्ब अनन्त पर बनता है।
अतः इस प्रकार u_e = f_e
समी. (3) में मान रखने पर,
m = \(\frac{f_{o}}{f_{e}}\) …………..(5)
इस स्थिति में दूरदर्शी की नली की लम्बाई = f_o + 4f + f_e

प्रश्न 10.
गैलीलियन दूरदर्शी का वर्णन निम्न शीर्षकों के अन्तर्गत कीजिए-
(i) प्रतिबिम्ब का किरण आरेख,
(ii) आवर्धन क्षमता के लिए व्यंजक।
उत्तर:
(i) प्रतिबिम्ब का किरण आरेख-

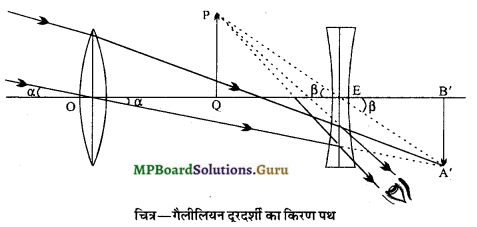
(ii) आवर्धन क्षमता – अन्तिम प्रतिबिम्ब द्वारा निर्मित दर्शन कोण और वस्तु द्वारा निर्मित दर्शन कोण के अनुपात को दूरदर्शी की आवर्धन क्षमता कहते हैं।

चूँकि वस्तु अनन्त पर है, अतः वस्तु द्वारा अभिदृश्यक पर बनाये गये कोण को वस्तु के द्वारा आँख पर बनाये गये कोण या दर्शन कोण के बराबर माना जा सकता है।

या m = \(\frac{\beta}{\alpha}\)
चूँकि α और β के मान बहुत ही कम होते हैं, अत: α = tanα तथा β = tanβ ले सकते हैं।
∴ m = \(\frac{\tan \beta}{\tan \alpha}\) …………(1)
चित्र से, tanβ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{EB}^{\prime}}\) तथा tanα = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{OB}^{\prime}}\)
समी. (1) में मान रखने पर,
m = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime} / \mathrm{EB}^{\prime}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime} / \mathrm{OB}^{\prime}}\)
या m = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{EB}^{\prime}} \times \frac{\mathrm{OB}^{\prime}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}\)
या m = \(\frac{\mathrm{OB}^{\prime}}{\mathrm{EB}^{\prime}}\) …………..(2)
परन्तु OB’ = + f_o = अभिदृश्यक की फोकस दूरी, EB’ = + u_e = प्रतिबिम्ब A’B’ की नेत्रिका से दूरी। समी. (2) में मान रखने पर,
m = …………….(3)

(a) जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने-मानलो नेत्रिका की फोकस दूरी है।
तब नेत्रिका के लिए, u = + u_e, v = -D तथा f = -f_e

इस स्थिति में दूरदर्शी की नली की लम्बाई = f_o – u_e.

(b) जब अन्तिम प्रतिबिम्ब अनन्त पर बने-
इस स्थिति में,
u_e = f_e
समी. (3) में मान रखने पर,
m = \(\frac{f_{o}}{f_{e}}\)
इस स्थिति में दूरदर्शी की नली की लम्बाई = f_o – f_e.

आंकिक प्रश्न

प्रश्न 1.
एक छोटे दूरदर्शी के अभिदृश्यक की फोकस दूरी 140 सेमी तथा नेत्रिका की फोकस दूरी 5 सेमी है। दूरस्थ वस्तु को देखने के लिये दूरदर्शी की आवर्धन क्षमता क्या होगी जबकि
(a) दूरदर्शी का समायोजन सामान्य है।
(b) अंतिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बनता है। (NCERT)
उत्तर:
दिया है – f_o =140 सेमी, f_e = 5सेमी, u_e = 25 सेमी,
(a) m = \(-\frac{f_{o}}{f_{e}}\)
m = \(-\frac{140}{5}\)
m = -28

(b) m = \(-\frac{f_{o}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)\)
m = \(-\frac{140}{5}\left(1+\frac{5}{25}\right)\)
m = -28(1 + 0.2) m
= -28 × 1.2
m = -33.67

प्रश्न 2.
एक खगोलीय दूरदर्शी की लम्बाई 80 सेमी है। यदि उसका आदर्धन 15 हो, तो अभिदृश्यक लेंस व नेत्रिका लेंस की फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया है : लम्बाई L= 80 सेमी
अर्थात् f_o + f_e = 80 सेमी
आवर्धन m = -15
तो सूत्र m = \(\frac{-f_{o}}{f_{e}}\) में मान रखने पर,
15 = \(\frac{f_{o}}{f_{e}}\)
⇒ f_o = 15f_e
चूँकी f_o + f_e = 80
∴ 15f_e + f_e = 80 या 16f_e = 80
या f_e = 5 cm
तो f_o = 75 सेमी होगा।

प्रश्न 3.
संयुक्त सूक्ष्मदर्शी के अभिदृश्यक की आवर्धन क्षमता 8 है। यदि संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता 32 हो, तो नेत्रिका लेंस की आवर्धन क्षमता ज्ञात कीजिए।
उत्तर:
दिया है – m_o= 8, m= 32, m_e = ?
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता
m = m_om_e …………(1)
समी. (1) में मान रखने पर,
32 = 8 × m_e
m_e = \(\frac{32}{8} .\)
m_e = 4

प्रश्न 4.
एक दूरदर्शी के अभिदृश्यक का व्यास 0.1 मीटर है तथा प्रकाश का तरंगदैर्घ्य 6000Å है। उसकी विभेदन सीमा कितनी होगी?
उत्तर:
सूत्र, विभेदन सीमा = \(\frac{1 \cdot 22 \lambda}{d}\)
दिया है-
λ = 6000Å = 6000 × 10^-10 m, d = 0. 1m
∴ विभेदन सीमा = \(\frac{1 \cdot 22 \times 6000 \times 10^{-10}}{0 \cdot 1}\)
= 7. 32 × 10^-6 रेडियन।

वस्तुनिष्ठ प्रश्न
1. सही विकल्प चुनकर लिखिए

प्रश्न 1.
एक संयुक्त सूक्ष्मदर्शी में अभिदृश्यक व नेत्रिका की आवर्धन क्षमताएँ क्रमशः m₁ व m₂ हैं सूक्ष्मदर्शी की आवर्धन क्षमता रहेगी
(a) m₁ + m₂
(a) m₁ – m₂
(b) m₁ × m₂
(c) \(\frac{m_{1}}{m_{2}}\)
उत्तर:
(c) \(\frac{m_{1}}{m_{2}}\)

प्रश्न 2.
किसी दूरदर्शी की विभेदन क्षमता निर्भर करती है-
(a) नेत्रिका की फोकस दूरी पर.
(b) अभिदृश्यक की फोकस दूरी पर
(c) दूरदर्शी की नली की लंबाई पर
(d) अभिदृश्यक के व्यास पर।
उत्तर:
(d) अभिदृश्यक के व्यास पर।

प्रश्न 3.
निकट दृष्टि दोष के निवारण हेतु प्रयुक्त किया जाता है-
(a) अवतल लेंस
(b) उत्तल लेंस
(c) बेलनाकार लेंस
(d) उपर्युक्त सभी।
उत्तर:
(a) अवतल लेंस

प्रश्न 4.
दूर दृष्टि दोष के निवारण हेतु प्रयुक्त किया जाता है-
(a) अवतल लेंस
(b) सामान्य काँच
(c) उत्तल लेंस
(d) इनमें से कोई नहीं।
उत्तर:
(c) उत्तल लेंस

प्रश्न 5.
एक स्वस्थ मानव नेत्र के लिए स्पष्ट दृष्टि की न्यूनतम दूरी होती है
(a) 50 सेमी
(b) 25 सेमी
(c) 25 मीटर
(d) अनंत।
उत्तर:
(b) 25 सेमी

प्रश्न 6.
किसी दूरदर्शी की न्यूनतम आवर्धन क्षमता M है। उसकी नेत्रिका की फोकस दूरी आधी कर देने पर उसकी आवर्धन क्षमता हो जायेगी-
(a) M/2
(b) 2M
(c) 3M
(d) 4M.
उत्तर:
(b) 2M

प्रश्न 7.
यदि अभिदृश्यक लेंस की फोकस दूरी बढ़ा दी जाये तो
(a) सूक्ष्मदर्शी की आवर्धन क्षमता बढ़ेगी किन्तु दूरदर्शी की घट जायेगी
(b) सूक्ष्मदर्शी और दूरदर्शी दोनों की आवर्धन क्षमता बढ़ जायेगी
(c) सूक्ष्मदर्शी और दूरदर्शी दोनों की आवर्धन क्षमता घट जायेगी
(d) सूक्ष्मदर्शी की आवर्धन क्षमता घटेगी किन्तु दूरदर्शी की बढ़ेगी।
उत्तर:
(d) सूक्ष्मदर्शी की आवर्धन क्षमता घटेगी किन्तु दूरदर्शी की बढ़ेगी।

प्रश्न 8.
एक संयुक्त सूक्ष्मदर्शी में अभिदृश्यक लेंस होता है-
(a) छोटे द्वारक का उत्तल लेंस
(b) बड़े द्वारक का उत्तल लेंस
(c) छोटे द्वारक का अवतल लेंस
(d) बड़े द्वारक का अवतल लेंस।
उत्तर:
(a) छोटे द्वारक का उत्तल लेंस

प्रश्न 9.
संयुक्त सूक्ष्मदर्शी में नेत्रिका की फोकस दूरी अभिदृश्यक की फोकस दूरी से-
(a) कम होती है
(b) अधिक होती है
(c) बराबर होती है
(d) इनमें से कोई नहीं।
उत्तर:
(b) अधिक होती है

प्रश्न 10.
साधारण दूरदर्शी की आवर्धन क्षमता बढ़ायी जा सकती है, यदि इस्तेमाल करें-
(a) अधिक फोकस दूरी की नेत्रिका
(b) छोटी फोकस दूरी की नेत्रिका
(c) अधिक व्यास की नेत्रिका
(d) छोटे व्यास की नेत्रिका।
उत्तर:
(b) छोटी फोकस दूरी की नेत्रिका

प्रश्न 11.
खगोलीय दूरदर्शी की आवर्धन क्षमता बढ़ाने के लिए-
(a) अभिदृश्यक की फोकस दूरी अधिक तथा नेत्रिका की फोकस दूरी कम होनी चाहिए
(b) अभिदृश्यक की फोकस दूरी कम तथा नेत्रिका की फोकस दूरी अधिक होनी चाहिए
(c) दोनों लेंसों की फोकस दूरियाँ कम होनी चाहिए
(d) दोनों लेंसों की फोकस दूरियाँ अधिक होनी चाहिए।
उत्तर:
(a) अभिदृश्यक की फोकस दूरी अधिक तथा नेत्रिका की फोकस दूरी कम होनी चाहिए

प्रश्न 12.
एक संयुक्त सूक्ष्मदर्शी या दूरदर्शी का अभिदृश्यक एक प्रतिबिम्ब I_O बनाता है और नेत्रिका एक
प्रतिबिम्ब I_e बनाती है, तो
(a) I_oआभासी है किन्तु I_e वास्तविक है
(b) I_o वास्तविक है किन्तु I_e आभासी है
(c) I_o और I_e दोनों वास्तविक हैं
(d) I_o और I_e दोनों आभासी हैं।
उत्तर:
(b) I_o वास्तविक है किन्तु I_e आभासी है

प्रश्न 13.
रीडिंग लेंस के लिए प्रयुक्त करते हैं-
(a) कम फोकस दूरी का अवतल लेंस
(b) अधिक फोकस दूरी का अवतल लेंस
(c) कम फोकस दूरी का उत्तल लेंस
(d) अधिक फोकस दूरी का उत्तल लेंस।
उत्तर:
(c) कम फोकस दूरी का उत्तल लेंस

प्रश्न 14.
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता अधिक होती है, यदि नेत्रिका की फोकस दूरी है
(a) अधिक
(b) कम
(c) अभिदृश्यक की फोकस दूरी के बराबर
(d) अभिदृश्यक की फोकस दूरी से कम।
उत्तर:
(b) कम

प्रश्न 15.
एक दूरदर्शी की सहायता से चन्द्रमा का फोटोग्राफ लिया गया। बाद में पाया गया कि दूरदर्शी के अभिदृश्यक पर एक मक्खी बैठ गई थी। फोटोग्राफ में-
(a) मक्खी का प्रतिबिम्ब दिखेगा
(b) चन्द्रमा के प्रतिबिम्ब की तीव्रता कम हो जायेगी
(c) कोई प्रभाव नहीं पड़ेगा
(d) मक्खी का आकार बढ़ जायेगा।
उत्तर:
(b) चन्द्रमा के प्रतिबिम्ब की तीव्रता कम हो जायेगी

प्रश्न 16.
स्वस्थ नेत्र की विभेदन-सीमा लगभग होती है-
(a) 1′
(b) 1″
(c) 1°
(d) \(\left(\frac{1}{60}\right)^{\prime \prime}\)
उत्तर:
(a) 1′

प्रश्न 17.
किसी दूरदर्शी का व्यास d तथा आवर्धन-क्षमता m है। यदि प्रकाश का तरंगदैर्घ्य 2 हो, तो इसकी विभेदन-क्षमता होगी1-22 1.22d
(a) \(\frac{1 \cdot 22 \lambda}{d}\)
(b) \(\frac{1 \cdot 22 d}{\lambda}\)
(c) \(\frac{\lambda m}{1 \cdot 22 a}\)
(d) \(\frac{a}{1 \cdot 22 \lambda m}\)
उत्तर:
(a) \(\frac{1 \cdot 22 \lambda}{d}\)

2. रिक्त स्थानों की पूर्ति कीजिए

1. स्वस्थ नेत्र की विभेदन सीमा ………. होती है।
उत्तर:
(एक मिनट) या \(\left(\frac{1}{60}\right)^{\circ}\)

2. जिन यन्त्रों की सहायता से निकटवर्ती या दूरवर्ती वस्तुओं को देखा जाता है, उन्हें ………… कहते हैं।
उत्तर:
प्रकाशीय यन्त्र

3. किसी वस्तु द्वारा नेत्र पर बनाये गये कोण को ………. कहते हैं।
उत्तर:
दर्शन कोण

4. ……… एक ऐसा उपकरण है, जिसकी सहायता से पास रखी सूक्ष्म वस्तुओं को आवर्धित रूप में स्पष्ट रूप से देखा जा सकता है।
उत्तर:
सूक्ष्मदर्शी

5. प्रतिबिम्ब द्वारा निर्मित दर्शन कोण और स्पष्ट दृष्टि की न्यूनतम दूरी पर रखी वस्तु द्वारा निर्मित दर्शन कोण के अनुपात को सूक्ष्मदर्शी की ………….. कहते हैं।
उत्तर:
आवर्धन क्षमता

6. सूक्ष्मदर्शी में अभिदृश्यक द्वारा हमेशा …….. प्रतिबिम्ब बनता है।
उत्तर:
वास्तविक

7. सूक्ष्मदर्शी तथा दूरदर्शी में नेत्रिका द्वारा हमेशा …….. प्रतिबिम्ब बनता है।
उत्तर:
आभासी

8. ………. दूरदर्शी में वस्तु का कहीं भी वास्तविक प्रतिबिम्ब नहीं बनता है।
उत्तर:
गैलीलियो

9. इलेक्ट्रॉन सूक्ष्मदर्शी की आवर्धन क्षमता, प्रकाशिक सूक्ष्मदर्शी की तुलना में ……. होती है।
उत्तर:
बहुत अधिक

10. संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता अभिदृश्यक लेंस और नेत्रिका की रैखिक आवर्धन के ………………. के बराबर होती है।
उत्तर:
गुणनफल

11. सरल सूक्ष्मदर्शी में वस्तु का प्रतिबिम्ब सीधा बनता है अतः इसकी आवर्धन क्षमता …………… होगी।
उत्तर:
धनात्मक

12. दूरदर्शी में अभिदृश्यक लेंस की फोकस दूरी नेत्रिका लेंस की फोकस दूरी से ……….. होती है।
उत्तर:
अधिक

13. एक स्वस्थ नेत्र के लिए स्पष्ट दृष्टि की न्यूनतम दूरी ……………. होती है।
उत्तर:
25 सेमी

14. खगोलीय दूरदर्शी के अभिदृश्यक लेंस के द्वारक (व्यास) बढ़ा देने पर इसकी ………… बढ़ जाती है।
उत्तर:
विभेदन क्षमता

15. एक संयुक्त सूक्ष्मदर्शी के अभिदृश्यक और नेत्रिका की आवर्धन क्षमताएँ क्रमशः m a m2 हैं।
सूक्ष्मदर्शी की आवर्धन क्षमता ………… होगी।
उत्तर:
m₁ × m₂

3. उचित संबंध जोड़िए

स्तम्भ ‘अ’	स्तम्भ ‘ब’
1. गैलीलियो दूरदर्शी की नेत्रिका	(a) 1 + \(\frac{\mathrm{D}}{\mathrm{F}}\)
2. सूक्ष्मदर्शी की विभेदन क्षमता	(b) \(\frac{d}{1 \cdot 22 \lambda}\)
3. दूरदर्शी की विभेदन क्षमता	(c) -\frac{v_{0}}{u_{0}}\left(1+\frac{\mathrm{D}}{f_{e}}\right)
4. सरल सूक्ष्मदर्शी की आवर्धन क्षमता	(d) \(\frac{2 \mu \sin \theta}{\lambda}\)
5. संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता	(e) अवतल लेंस।

उत्तर:
1. (e) अवतल लेंस
2. (d) \(\frac{2 \mu \sin \theta}{\lambda}\)
3. (b) \(\frac{d}{1 \cdot 22 \lambda}\)
4. (a) 1 + \(\frac{\mathrm{D}}{\mathrm{F}}\)
5. (c) -\frac{v_{0}}{u_{0}}\left(1+\frac{\mathrm{D}}{f_{e}}\right)