MP Board Class 12th Physics Important Questions Chapter 1 Electric Charges and Fields

MP Board Class 12th Physics Important Questions Chapter 1 Electric Charges and Fields

Electric Charges and Fields Important Questions Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The least charge is:
(a) 1 coulomb
(b) 1 stat coulomb
(c) 1 micro coulomb
(d) Electronic charge.
Answer:
(d) Electronic charge.

Question 2.
The number of electrons in one coulomb charge is:
(a) 5.46 × 10²⁹
(b) 6.25 × l0¹⁸
(c) 1.6 × l0¹⁹
(d) 9.0 × l0²⁹
Answer:
(b) 6.25 × l0¹⁸

Question 3.
An object has – 80 µ C.What is the excess number of electrons:
(a) 5 × 10⁸C
(b) 16 × 10¹⁴C
(c) 5 × 10¹⁴ C
(d) 16 × 10⁸C.
Answer:
(c) 5 × 10¹⁴ C

Question 4.
The intensity of electric field E due to charge Q at distance r as compared to its normal state:
(a) E ∝ r
(b) E ∝ \(\frac { 1 }{ { r }^{ 2 } } \)
(c) E ∝ \(\frac { 1 }{ r }\)
(d) E ∝ \(\frac { 1 }{ { r }^{ 3 } } \)
Answer:
(b) E ∝ \(\frac { 1 }{ { r }^{ 2 } } \)

Question 5.
The value of permitivity E₀ of vacuum (or free space) is :
(a) 8.85 × 10^-12 C
(b) 8.85 × 10^-12C²N^-1m^-2
(c) 9 × 10⁸ Nm²C^-2
(d) 9 × 10 C²N^-1m^-2.
Answer:
(b) 8.85 × 10^-12C²N^-1m^-2

Question 6.
The work done in rotating a dipole of dipole moment p through an angle 180° from direction of uniform electric field E is:
(a) 2pE
(b) pE
(c) \(\frac { 1 }{ p}\)pE
(d) Zero.
Answer:
(a) 2pE

Question 7.
The intensity of electric field E due to a dipole of dipole moment p at a point a distance r from center of dipole depends on r as :
(a) E ∝ r
(b) E ∝ \(\frac { 1 }{ { r }^{ 2 } } \)
(c) E ∝ \(\frac { 1 }{ r }\)
(d) E ∝ \(\frac { 1 }{ { r }^{ 3 } } \)
Answer:
(d) E ∝ \(\frac { 1 }{ { r }^{ 3 } } \)

Question 8.
A surface S is placed in an electric field E parallel to the field. The flux linked with the surface be:
(a) ES
(b) \(\frac{ E }{S}\)
(c) Zero
(d) Infinite.
Answer:
(c) Zero

Question 9.
The total electric flux emerges out from unit positive charge in air is:
(a) E₀
(b) \(\frac { 1 }{ { E }_{ 0 } } \)
(d) \(\frac { 1 }{ { 4\pi E }_{ 0 } } \)
(d) 4πE₀
Answer:
(b) \(\frac { 1 }{ { E }_{ 0 } } \)

Question 10.
The dielectric constant of metal is:
(a) Infinite
(b) Zero
(c) One
(d) None of these.
Answer:
(a) Infinite

Question 11.
The dielectric constant of air is:
(a) 8.85 × l0^-12 C² N^-1m^-2
(b) 1
(c) Infinite
(d) None of these
Answer:
(c) Infinite

Question 2.
Fill in the blanks:

1. The dimensional formula of charge is …………….
2. The two like charges …………… each other.
3. Two unlike charges ……………. each other.
4. The SI unit of electric field is …………….
5. The dimensional formula of electric field is …………….
6. The size of an ideal dipole is …………….
7. Two charges – q and + q are situated at a distance / its dipole moment will be …………….
8. The size of an ideal dipole is …………….
9. Two charges – q and + q are situated at a distance lits dipole moment will be …………….
10. The maximum torque acting on a dipole of dipole moments p in a uniform electric field E is …………….

Answers:

1. [AT]
2. Repel
3. Attract
4. NC^-1
5. [ML^-3A^-1’]
6. Point size
7. q.I
8. pE sin G.

Question 3.
Match the Column:

Answers:
(b) newton / coulomb
(e) coulomb
(a) coulomb x metre
(d) N – m²/C
(c) coulomb²/newton x meter ²

answers:

1. (e) \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { { q }_{ 1 }{ q }_{ 2 } }{ { Kr }^{ 2 } }\)
2. (d) \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { q }{ { Kr }^{ 2 } } \)
3. (b) \(\frac { q }{ { E }_{ 0 } } \)
4. (c) pE(1 – cosθ)
5. (a) – pE cos θ

Question 4.
Write the answer in one word / sentence:

1. What type of charge get accumulated in a glass rod rubbed with silk ?
2. What type of charge get accumulated in rubber rod when rubber with fur fabric ?
3. What is the cause of quanti zation of charge ?
4. What is dielectric constant of a metal ?
5. What is the direction of electric dipole moment ?

Answers:

1. Positive charge
2. Negative charge
3. Transfer of electrons takes place in integral multiple. This is the cause of quantization
4. Infinity
5. Direction of dipole moment is from negative charge to positive charge

Electric Charges and Fields Important Questions Very Short Answer Type Questions

Question 1.
What does q₁ + q₂ = 0 signify in electrostatics ?
Answer:
The equation signifies that the electric charges are algebraically additive and here q₁ and q₂ are equal and opposite.

Question 2.
Why electric lines of force do not form closed loop ? (AH India 2014)
Answer:
Because electric lines of force start from the positive charge and end on die negative charge.

Question 3.
Why must electrostatic field at the surface of charged conductor be perpendicular to every point on it ? (Foreign 2014)
Answer:
As, electric field inside a conductor is always zero. So electric lines of force exert lateral pressure on each other and hence repulsion between like charges take place. Thus, in order to stable the spacing, the lines of force are normal to surface.

Question 4.
What quantity is electric flux ? Write its SI unit.
Answer:
It is a scalar quantity. S.I. unit of electric flux is Nm²/C 

Question 5.
Charge of on QNC is placed as centre of a cube. What will be the electric flux passing through a face of it ?
Answer:

Question 6.
Charges +q₁ -5q₁, +2q and +2q is at Gaussian surface. What will be the magnitude of electric flux passing through Gaussian surface.
Answer:
Zero, because total charges is zero as surface of Gaussian surface.

Question 7.
Fig. shows three charges + 2q, – q and+ 3q. Two charges T 2q and – q are enclosed within a surface S. What is the electric flux through the surface S ?
Answer:

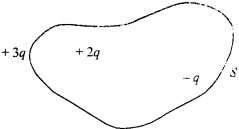
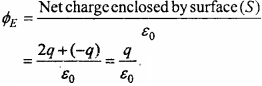
Question 8.
Does charge get changes with the velocity of charged conductor ?
Answer:
No? charge does not get change with velocity of charged conductor.

Question 9.
Which scientist first discovered the charge as positive and negative ?
Answer:
Benjamin Franklin.

Question 10.
Is static electric force is Newtonian between two charges ?
Answer:
Yes, static electric force Newtonian between two charges.

Question 11.
What is the relation between dielectric constant in vacuum and medium ?
Answer:
£ = £₀ × £_r

Question 12.
What is the electric force acting upon charge q placed in electric field E ?
Answer:
qE

Electric Charges and Fields Important Questions Short Answer type Questions

question 1.
Write the limits of inverse square law ?
Answer:

• It is true only for point charge.
• It is only for that charges which is at rest.

Question 2.
Write the basic properties of electric charge ?
Answer:

• Quantization of charge i.e. q = ±ne.
• Charge cannot be created nor be destroyed.

Question 3.
What is dielectric constant of a metal ?
Answer:
The dielectric constant of a metal is ∞

Question 4.
Define intensity of electric field and write its unit.
Answer:
The electric field intensity at a point due to a source charge is defined as the force experienced by a unit positive test charge placed at that point. If \(\overrightarrow{\mathrm{F}}\) is the force acting on test charge qo placed at a point in the electric field of intensity\(\overrightarrow{\mathrm{E}}\) then \(\overrightarrow{\mathrm{E}}\) = \(\frac{\overrightarrow{\mathrm{F}}}{q_{0}}\)
Unit: Its S.I. unit is newton/coulomb.

Question 5.
What is an electric dipole ?
Answer:
A system of two equal and opposite charges kept very close to each other is • called an electric dipole.

Question 6.
What is an electric flux ? Give its SI Units.
Answer:
Electric flux associated with electric field is a measure of total lines of force passing normally to the surface, when held in the electric field. Its SI unit is newton meter per coulomb.

Question 7.
What do you mean by quantization of electric charge ?
Answer:
Quantization of electric charge means that the total charge (q) of a body is always ah integral multiple of basic charge (e) which is the charge on the electron.
.’. Charge on any body, q = ± ne
Where, e = 1.6 x 10^-19 coulomb and n = 0,1,2,3 In above relation, +ve sign denotes the loss of electrons and – ve sign denotes gain of electrons. certain particles are known having these charges which are called quarks.
Charge on any body will never be a fraction of e Like \(\frac { 3 }{ 2 }\)e, \(\frac { 5 }{ 2 }\)e, \(\frac { 7 }{ 2 }\)e. But, now days, certain particles are known having these charges which are called quarks.

Question 8.
Ordinary rubber are insulators but the types of an aeroplane are made a little bit conducting. Why ?
Answer:
When the aeroplane lands and takes off, the friction between types and the run-way may cause the electrification of types. Due to conducting nature of the types, the charge so produced is conducted to the earth and electrical sparking is avoided.

Question 9.
State Gauss’ theorem in electrostatics.
Answer:
The net electric flux passing through any closed surface is \(\frac { 1 }{ { E }_{ 0 } } \) times the net charge present inside it. Mathematically,

Question 10.
The mass of an isolated conductor decreases when some positive charge is given to it. Why ?
Answer:
Mass will reduce because when electrons escape out from the conductor then only it becomes positively charged.

Question 11.
Write the nature of the force acting between q₁ and q₂ if –

1. q₁ q₂ > 0
2. q₁q₂ <0
3. q₁q₂ = 0.

Answer:

1. If q₁q₂ > 0, then both charges are similar and repulsive force acts in between them.
2. If q₁ q₂ < 0, then both charges are of opposite nature and attractive force acts in between them.
3. If q₁q₂ = 0 then one of the two charges is neutral and no force acts in between them.

Question 12.
State principle of conservation of charges. Give examples.
Answer:
According to principle of conservation of charge “Net charge in any isolated system always remains constant”. In the other words “Charge can neither be created nor be , destroyed although it may be transferred from one body to another body”.

Example:
1. Pair annihilation:
When an electron and a positron come near to each other, then they get destroyed and form a y ray photon. Thus the total charge becomes zero.

2. Pair production:
A gamma ray photon splitted into a positron and an electron

Question 13.
Define electric dipole moment. Is it scalar or vector ? Write its SI unit and dimensional formula.
Answer:
Electric dipole moment is the product of magnitude of any one charge of dipole and the distance between both the charges. If + q and – q are two charges placed at a distance 2l apart, then electric dipole moment will be
\(\vec{p}\) = q. 2l

It is a vector quantity whose direction is from negative charge to positive charge.
Unit: Its SI unit is coulomb – meter.
Dimension: [p] = [q][2l] = [ATL]
|p] = [M⁰L¹T¹A¹].

Question 14.
Metallic ropes are attached with the vehicles carrying inflammable substances, connected to earth. Why ? (NCERT)
Answer:
Moving vehicles get charged due to friction. The inflammable material may catch fire due to spark produced by charged vehicle. When metallic ropes or chain is used, the charge developed on the vehicle is transferred to the ground and so the fire is prevented.

Question 15.
When the electric dipole becomes in equilibrium state when kept in electric field?
Answer:
We know that U = – pE cosθ
When the angle between electric dipole and electric field is zero then the electric dipole will be in equilibrium.

Question 16.
State Coulomb’s inverse square law of electrostatic charges. On this basis define unit charge. What is the condition for the law to be applicable ?
Answer:
Coulomb’s inverse square law:
According to it, force of attraction or repulsion between two point charges is directly proportional to the product of their magnitude and inversely proportional to the square of distance between them. Force of attraction or repulsion is the central force which acts along the line joining the two charges. Let the charges q₁ and q₂ be placed at a distance r apart from each other. So, the force acting between them according to Coulomb’s law will be
F ∝ q₁q₂ and F ∝ \(\frac { 1 }{ { r }^{ 2 } } \)

Combining the above two relations, we get

To define unit charge : Let q₁ = q₂ = q, r = lm and F = 9 x 10⁹ newton.
Putting these values in eqn. (1), we get
9 x 10⁹N = 9 × 10⁹ × \(\frac { { q }^{ 2 } }{ { 1m }^{ 2 } } \)
q = ±1 coulomb
So, if two charges of same type and equal magnitude are placed at 1 m apart in vacuum and if force of repulsion between them is 9 × 10⁹ newton, then the two charges are said to be unit charges of magnitude 1 coulomb.

Condition for the applicability of the law:

• It is applicable for the point charges which are stationary’, not for moving charges.
• It is not valid for large distances and distances less than 10^-15 meter because at distances less than 10^-15 m, nuclear forces are dominant.

Question 17.
Define intensity of electric field and write its unit Four properties of electric lines of force.
Answer:
The electric field intensity at a point due to a source charge is defined as the force experienced by a unit positive test charge placed at that point. If \(\overrightarrow{\mathrm{F}}\) is the force acting on test charge q placed at a point in the electric field of intensity \(\overrightarrow{\mathrm{E}}\) then \(\overrightarrow{\mathrm{E}}\) =\(\frac{\overrightarrow{\mathrm{F}}}{q_{0}}\)
Unit: Its SI unit is newton / coulomb.

Properties:
(a) Electric lines of force start from positive charge and end on negative charge.
(b) Tangent drawn at any point of the lines of force gives the direction of electric field intensity.
(c) Two lines of force will never intersect each other.
(d) Lines of force try to contract longitudinally. This demonstrates why unlike charges attract each other.
(e) They are emitted normal to the surface of conductor and end normally.

Question 18.
Why the two lines of force do not cross or intersect each other ?
Answer:
If two lines of force intersect, then there would be two tangents and hence two directions of electric field at the point of intersection, which is not possible.

Question 19.
Prove that electrostatic force is much stronger than the gravitational force.
Or
Compare the electrostatic force and gravitational force.(NCERT)
Answer:
Let a proton and an electron be placed in air or vacuum at lm distance apart, mass of proton and electron are mp and me respectively.
m_p = l.67 × 10^-27 kg
m_e = 9.1 × 10^-31 kg
Charge on proton is q_p = 1.6 ×10^-19C. and charge on electron is q_e = 1.6 x 10^-19C The electrostatic force acting between them is –
\(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { { q }_{ p }{ q }_{ e } }{ { Kr }^{ 2 } }\)

The gravitational force between proton and electron is –

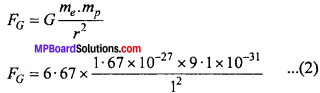
Dividing eqn. (1) by eqn. (2), we get

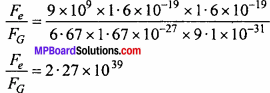
F_e = 2.27 × l0³⁹ × F_G
Thus, the electrostatic force of attraction is 1039 times more than the gravitational force for the electron – proton system. Obviously the electrostatic force acting between two charged particles is very much greater than the gravitational force acting between them.

Question 20.
(a) Define electric flux. Write its SI unit and dimensional formula.
Answer:
Electric flux associated with the electric field is a measure of total lines of force passing normally to the surface, when held in the electric field. It is denoted by Φ_E If the normal drawn to the surface dS makes an angle 0 with the electric field E, then the flux through this area is –
dΦ_E = \(\overrightarrow{\mathrm{E}}\).\(\overrightarrow{\mathrm{dS}}\)
Unit: Its SI unit is Nm²/ C.

Dimension:

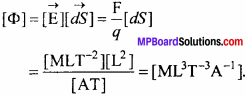
Question 20. (b)
Under what conditions flux is said to be positive and negative ?
Answer;
Electric flux:
The electric flux associated with a surface is a measure of total lines of force passing normally to the surface when held in the electric field. It is denoted by ∅_E There are two types of electric flux:

• Positive electric flux – When electric lines of force leaves any body through its surface, it is considered as positive flux.
• Negative electric flux – When electric lines of force enters into body through any surface, it is considered as negative flux.

Question 20. (c)
Show that the electric flux passing through a surface parallel to electric field is zero.
Answer:
Let \(\overrightarrow{\mathrm{E}}\) be the intensity of electric field and \(\overrightarrow{\mathrm{dS}}\) be the normal to the arbitary surface. If the normal to the surface (\(\overrightarrow{\mathrm{dS}}\)) marks an angle θ with E, then,
The electric flux can be given by
d∅_E = E. dS cos θ
If surface is parallel to the electric field
i.e., θ = 90°
d∅_E = E dS cos 90°
= E.dS × 0
d∅_E = 0

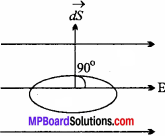
Thus flux passing through a parallel surface to an electric field is zero.

Question 21.
State the principle of electrostatic shielding.
Answer:
The electric field inside the charged hollow conductor (spherical shell) is zero. Therefore, when an object is placed inside a hollow conductor then there will be no effect of electric field on the object i.e., the hollow conductor shields the object from external electric field.

The concept of electrostatic shielding is used to shield wires carrying audio signal from external fields like atmospheric electricity or due to electric sparks. If such wires are not shielded, the audio signal will give rise to noisy sound or reproduction.

Question 22.
Derive an expression of electric field intensity on a point in axial position (end on position) of an electric dipole.
Answer:
Consider an electric dipole made up of charges + q and – q separated by a distance 2/apart and placed in vacuum. We have to find out the electric field at point P situated at a distance r from the center of dipole system. To find out the electric field intensity, imagine a unit positive test charge situated at P.

Electric field intensity due to charge (+q) situated at A will be

Electric field intensity due to charge (-q) situated at B will be 1

As AP < PB, hence repulsive effect due to charge +q will be more effect then the attractive effect of charge – q. Therefore, E₁> E₂ but their directions are opposite. Hence, the net electric field will be

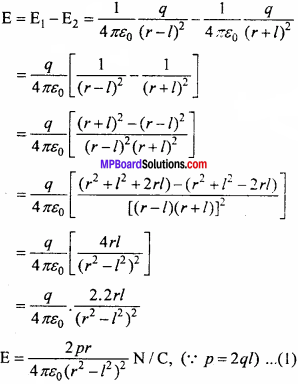
This is the expression for the electric field which is directed from A to P. For small and strong dipoles,
r>>2l ⇒ r>>l ⇒ r² >>>l²
∴ r² – l² ≈ r²
Hence, eqn. (1) becomes

This is the required expression.

Question 23.
Derive the expression for the intensity of electric field on the equatorial position of the dipole.
Answer:
Equatorial position is a point on the line which lies on the perpendicular bisector of the axial line, then their position is called equatorial position or broadside on position. Let AB be an electric dipole formed by charges +q and -q. The distance between the charges is 21. P is a point on the equatorial position of the dipole, situated at a distance r from the center of the dipole. Sup- pose unit positive test charge is situated at P. Electric field at P due to +q charge will be

Electric field at P due to -q charge will be


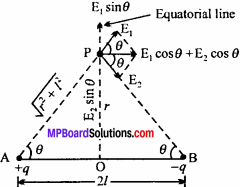
Resolving E and E₂ into its components, we get the component of E₁ are E₁cosθ parallel to AB and E₁ sin θ along OP. Also, components of E₂ are E₂ cosθ parallel to AB and E₂ sin O along PO.
From eqns. (1) and (2), we find |E₁| = |E₂|, hence E₁ sinθ = E₂ sinθ , but their directions are opposite. So, they cancel each other. The only resultant electric field will be
E = E₁ cos θ + E₂ cos θ
= E₁ cosθ + E₁ cos θ
E = 2E₁ cos θ  …………(3)

If the charges are kept in any other medium other than vacuum, then the electric field becomes

The direction of electric field is along AB i.e., it is parallel to axial line which acts from positive charge to negative charge. For small and strong dipoles, r >> 2l ⇒ r >> l
r2 + l2 ≈ r2
Hence, eqn. (4) becomes

Question 24.
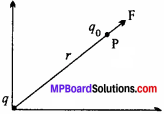
Obtain an expression for the intensity of electric field due to a charge q at a distance r from it.
Answer:
Consider a point charge q which is placed at the origin O of the generalized coordinate system. We have to find out the electric field at point P at a distance r from it. For this, imagine a test charge q₀ placed at point P. Both the charges q and q₀ have been placed in vacuum. According to Coulomb’s law, the force on charge q₀ will be

Where, r is the unit vector in the direction from q to q₀. But intensity of electric field is given by the formula,

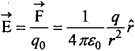
If any other medium is present having dielectric constant then

Where, £0 = k = dielectric constant of the medium. In magnitude,

Question 25.
Derive the expression for the torque acting on the dipole when kept in a uniform electric field and hence define dipole moment.
Answer:
Consider an electric dipole made up of charges +q and -q and length 2l which is placed in a uniform electric field of strength E. The dipole moment P makes an angle Q with respect to the electric field at any instant of time. As a result, a pair of forces +qE (along the direction of electric field) and -qE (opposite to the direction of electric field) acts on the dipole. These two opposite forces are of equal magnitude. So, they apply a couple on electric dipole, which tries to bring it along the direction of electric field. This couple is called restoring couple.

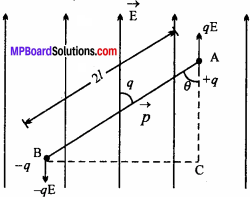
So, moment of couple or torque (τ)
= Magnitude of any force x Perpendicular distance between the forces
= qE × BC …….(1)
In A ABC, sinθ = \(\frac { BC }{ AB }\)
⇒ BC = AB sinθ = 2l sinθ
Putting the value of BC in eqn. (1), we get,
τ= qE × 2l sin θ
⇒ τ = pEsin θ,
(∴q 2l = p, where p is the dipole moment) ……..(2)
In vector form,
\(\overrightarrow{\mathrm{τ}}\) = \(\overrightarrow{\mathrm{p}}\) × \(\overrightarrow{\mathrm{E}}\)
From eqn. (2), if E = 1 and 0= 90°.Then,
τ = p sin 90° = p
Thus, dipole moment of an electric dipole is numerically equal to the torque acting on the dipole when it is placed perpendicular to a unit electric field.

Question 26.
Derive an expression for the potential energy of a dipole in an electric field.
Answer:
Work done in rotating any electric dipole from standard position to any angle with respect to the electric field is called potential energy. The standard position is considered to θ = i.e., perpendicular to the field. Let p be the dipole moment of the dipole, placed in an electric field of intensity E and it makes an angle θ with respect to the electric field, then
Torque, τ = p E sinθ
Also, work done in displacing the dipole through an angle dθ will be
dW = τdθ = pE sinθ dθ
Now, the work done in displacing from θ = \(\frac { π }{ 2 }\) to θ = θ is

This work done is stored in the form of potential energy,
U = – p E cosθ
In vector form, U = \(\overrightarrow{\mathrm{-p}}\).\(\overrightarrow{\mathrm{E}}\)
This is the required expression.

Question 27.
Derive the expression for the amount of work done in rotating a dipole in a uniform electric field.
Answer:
If a dipole placed in a uniform electric field is rotated from the equilibrium position, then work has to be done. Consider an electric dipole of dipole moment p(= 2 ql) which has been rotated in an electric field E by an angle 0 from the equilibrium position, then torque acting on it will be –
\(\overrightarrow{\mathrm{τ}}\) = \(\overrightarrow{\mathrm{-p}}\) × \(\overrightarrow{\mathrm{E}}\) = pE sin θ, (in magnitude form)
Work done in rotating the dipole through an angle dθ is
dw = τ.dθ
Therefore, work done in rotating it by an angle θ can be obtained from the above equation under proper limits.

Above equation is the total work done in rotating any electric dipole through an angle θ

Question 28.
Write and prove Gauss’ theorem.
Or
Prove that net electric flux through any closed surface is 1 / £₀ times of total charge present inside it, where s £₀ is
permittivity of free space.
Answer:
Gauss’ law:
According to Gauss’ law, the net electric flux through any closed surface is 1 / £₀ times of the total charge present inside it.

Where, £₀ is permittivity of vacuum or air.
Proof:
Let at any point O, inside any closed surface, a charge +q is present. A point P lies at a distance r from O on surface dS. Normal to the surface dS can be represented by \(\overrightarrow{\mathrm{dS}}\) (say). Therefore, electric field at point P due to charge +q can be given by

.’. Electric flux passing through area \(\overrightarrow{\mathrm{dS}}\)will be
dΦ_E = \(\overrightarrow{\mathrm{E}}\).\(\overrightarrow{\mathrm{dS}}\) = E dS cos0

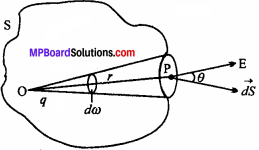
Where, 0 is an angle between electric field f and the normal to the surface.
Net flux through the closed surface is.

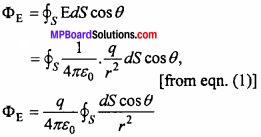
But \(\frac { dscos\theta }{ { r }^{ 2 } } \) = dw is the solid angle subtended by the small surface dS at O.

As total solid angle subtended by any closed surface at any point inside it is 4π hence –

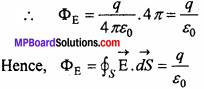
Above equation is mathematical form of Gauss’ law.

Electric Charges and Fields Important Questions Long Answer Type Questions

Question 1.
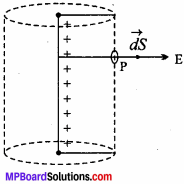
Obtain an expression for the intensity of electric field due to linear charge distribution.
Answer:
Consider a thin wire of length ‘l’ Let the charge given to it be q. So, the linear charge density will be λ = \(\frac { q }{ l }\) ⇒ q = λl
If a test charge ¡s brought near to the wire, then it will be repelled. Hence, the electric field (\(\overrightarrow{\mathrm{E}}\)) will be radially out ward. Draw a normal \(\overrightarrow{\mathrm{dS}}\) on the surface at P. The direction of \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{dS}}\) are the same. The electric flux passing through the curved surface of the cylinder is

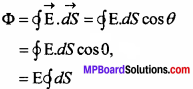
= E 2πrl (∴\(\overrightarrow{\mathrm{dS}}\) = Total surface areaofcurved surface 2,πrl …(2)
But according to Gauss’ theorem,
Φ = \(\frac { 1 }{ { E }_{ 0 } } \) x (Total charge present inside the Gaussian surface) …(3)
Φ = \(\frac { q }{ { E }_{ 0 } } \)
From eqns. (2) and (3), we have
E 2πrl = \(\frac { q}{ { E }_{ 0 } } \)
E 2πrl = \(\frac { λl}{ { E }_{ 0 } } \)
[∴q = λl from eqn. (1)]

This is the expression for the electric field due to a linear charge distribution having a linear charge density λ.

Question 2.
Derive an expression for the intensity of electric field due to a uniform infinite plane sheet of charge.
Answer:
Consider an infinite plane sheet on which charge given is q. If S is the total surface area of the sheet, then the surface charge density will be σ = \(\frac {q }{ S}\) = \(\frac { charge }{ area }\) the charge will be distributed uniformly on the surface of the sheet. Hence, surface charge density (= σ) remains constant. Any test charge held near to the surface will be repelled on both the sides i.e., either to paper and the other will go inside, hence the Gaussian surface formed will be cylindrical; which is having three surfaces S₁, S₂ and S₃.

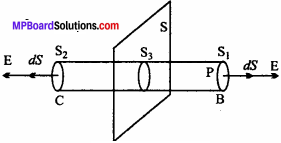
The electric field \(\overrightarrow{\mathrm{dS}}\) is directed radially outwards away from the sheet. Moreover, \(\overrightarrow{\mathrm{dS}}\) is the outward drawn normal on the Gaussian surface. Hence, the total electric flux is

The angle between normal to the curved surface S3 in the direction of electric field \(\overrightarrow{\mathrm{E}}\)] is 90°, hence

For the surfaces Sj and S2, \(\overrightarrow{\mathrm{E}}\) and\(\overrightarrow{\mathrm{dS}}\) are along the same direction, hence the angle between \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{dS}}\) is 0°, so

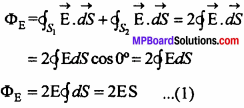
By Guss’ theorem,
Φ_E = \(\frac { 1}{ { E }_{ 0 } } \) q ……(2)
from eqns. (1) and (2) we get
2ES = \(\frac { q}{ { E }_{ 0 } } \)
E = \(\frac{q}{2 \varepsilon_{0} S}\)
Hence, E = \(\frac { σ}{ { 2E }_{ 0 } } \)
(∴ σ = \(\frac { q }{ S }\))
This is the expression for the intensity of electric field due to a uniformly charged Sheet

Question 3.
Prove that intensity of field is zero inside a spherical shell, while in outside it is such that all the charges are concentrated at the center.
Or
Determine the intensity of electric field by Gauss’ law, due to a uniformly charged spherical shell at a point

1. Outside the shell
2. On the surface of shell
3. Inside the shell.

Draw a graph showing the variation of electric field with the distance from the center.
Answer:
Intensity of electric field due to uniformly charged spherical shell:
Suppose that a sphere of radius R is uniformly charged with +q charge. Intensity at any point due to this charged sphere depends on its position relative to the sphere.

(i) When point P lies outside the spherical shell:
Consider a point P which lies outside the spherical shell of radius R. Now, imagine a sphere of radius r which passes through P. This closed surface behaves as Gaussian surface. Since, sphere is uniformly charged, so that electric field at each point on the surface is equal and points radially outward.

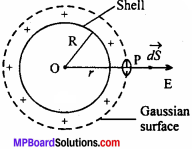
Net flux through the Gaussian sphere of radius r will be

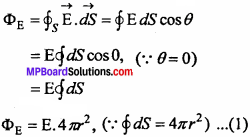
But, charge enclosed inside the Gaussian surface is q. Therefore, from Gauss’ law
Φ_E = \(\frac { q }{ { E }_{ 0 } } \) …….(2)
Equating eqns. (1) and (2), we have
E. 4πr² = \(\frac { q }{ { E }_{ 0 } } \)
E = \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { q }{ { r }^{ 2 } } \) ……..(3)

It is clear from above equation that, the electric field outside any uniformly charged spherical shell is exactly to that electric field when we take the same charge at the center of sphere.

(ii) Point P lies on the surface of spherical shell:
In this case, r = R
From eqn. (3),
E = \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { q }{ { R }^{ 2 } } \)

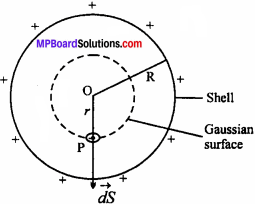
(iii) When point P lies inside the spherical shell:
As we know, the charge given to spherical shell spreads equally all over the surface, there is no charge present inside the sphere. Hence, by Gauss’ law,


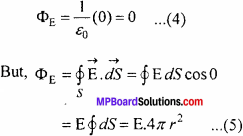
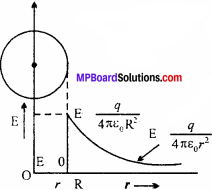
From equs. (4) and (5),
E.4πr² =  0
⇒ E = 0
Therefore, electric field inside a spherical shell is always zero. The adjacent figure shows the variation of electric field with distance.

Question 4.
Obtain an expression for the intensity of electric field due to a solid sphere of charge using Gauss’ theorem at the following points:

1. Outside the sphere
2. On the surface of sphere
3. Inside the sphere.

Also prove that the intensity of the electric field at the center will be zero.
Answer:
Suppose that a sphere of radius R is uniformly charged with +q charge. Intensity of electric field at any point depends on its position with respect to sphere. The volume charge density of sphere is
p = \(\frac { Charge }{ volume }\)

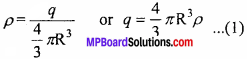
(i) When the point lies outside the sphere:
Consider a point P which lies outside the spherical shell of radius R. Now imagine a sphere of radius r which passes through P.This closed surface behaves as a Gaussian surface. The electric field at each point outside the sphere points radially outwards.

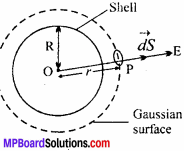
.’. Total flux through the Gaussian sphere of radius r will be –

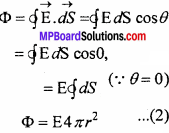
But charge enclosed inside the Gaussian surface is q. Hence, from Gauss’ law
Φ = \(\frac { 1}{ { E }_{ 0 } } \) q …..(3)
From eqns. (2) and (3),
E 4πr² = \(\frac { q}{ { E }_{ 0 } } \)
E = \(\frac { q }{ { 4\pi { E }_{ 0 }r }^{ 2 } }\)
Hence, the electric field outside any uniform charged sphere is same as if the entire charge is present at the centre.
Putting the value of q from eqn. (1) in eqn. (4), we get

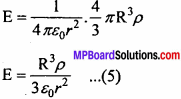
(ii) When the point lies on the surface of sphere:
r = R
From eqn. (4), we have E =

and from eqn. (5), we have E =

(iii) When the point lies inside the sphere:
Suppose the point P lies at a distance r from the center of the sphere such that r < R. At radius r draw a Gaussian surface which is a sphere. Then electric field \(\overrightarrow{\mathrm{E}}\) is radially outwards. Moreover, normal to surface \(\overrightarrow{\mathrm{dS}}\) is along the direction of \(\overrightarrow{\mathrm{E}}\). Hence, angle between \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{dS}}\) is 0°
The flux coming out of the Gaussian surface is –

But by Gauss’ law, the flux Φ = \(\frac { 1}{ { E }_{ 0 } } \) x (Total charge inside the Gaussian surface)
Φ = \(\frac { q}{ { E }_{ 0 } } \) q ……(2) (where q’ is the total charge inside the sphere of radius r)
On volume \(\frac { 4 }{ 3 }\) πR³charge given is q
On volume 1, charge given is = \(\frac { q }{ \frac { 4 }{ 3 } \pi R^{ 3 } } \)
On volume\(\frac { 4 }{ 3 }\) πR³ nr charge given is = \(\frac { q }{ \frac { 4 }{ 3 } \pi R^{ 3 } } \) x \(\frac { 4 }{ 3 }\) πR³ = \(\frac { q{ r }^{ 3 } }{ { R }^{ 3 } } \)
q’ = \(\frac { q{ r }^{ 3 } }{ { R }^{ 3 } } \)
‘Putting the value of q’ in.eqn. (2), we get
Φ = \(\frac { q}{ { E }_{ 0 } } \) \(\frac { q{ r }^{ 3 } }{ { R }^{ 3 } } \) …….(3)
from equs. (1) and (3) we get,

At the center of sphere, r = 0, hence E = 0.

Question 5.
Neeta return home from school. When she was taking out the sweater, she heard twinkling sound. She asked her mother but she was unable to answer.Next day she went to school and asked the science teacher, she was satisfied with her answer. Write down the answer of the question given below on the basis of above statement:

1. What values does she show ?
Answer:
She shown the value of answer, questioning.

2. What was the reason for the sound when she was taking out her sweater ?
Answer:
Due to the friction between her school dress and sweater, its acquire negative charge which get discharge. Therefore the sound was been listen by her.

3. Presence of charge can be determined by which apparatus ?
Answer:
Gold leaf electroscope.

4. Does any new charges get created on rubbing ? If yes or not than why ?
Answer:
No, new charges get created, only transfer of electron occur form one body to another. There one become positive charge and other become negative charge.

Electric Charges and Fields Important Questions Numerical Questions

Question 1.
Two positive ions which have same charges having a force of repulsion of
3.7 × 10^-9N. The distance between them is 5 Å. Find the deficiency of electron on each ions.
Solution Given:
F = 3.7 × 10^-9N, r = 5Å = 5 × 10^-10m
q₁ = q₂ = q

= 10.28 × 10³⁸
q = 3.2 × 10^-19
n = \(\frac { q }{ e }\)

There will be deficiency of two electron in each ions.

Question 2.
Calculate force of repulsion between two protons when they are separated with 4.0×10¹⁵m.
Solution:
We know that, \(\frac { 1 }{ 4\pi { E }_{ 0 } } \) = 9 × 10⁹Nm²C^-2
Given: q₁= q₂ = +1.6 × 10^-19 C,r = 4.0 × 10^-15m.
From formula, F = \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { { q }_{ 1 }{ q }_{ 2 } }{ { Kr }^{ 2 } }\)

or F = 14.4 newton.

Question 3.
Can 1 coulomb of charge be gives to a metallic sphere of radius 1cm? Give reason.
Solution:
Here, q = 1 C, r = lcm = 10^-2m
Electric field on the surface of sphere is
E = \(\frac { 1 }{ { 4\pi E }_{ 0 } }\) \(\frac { q }{ { r }^{ 2 } } \)
= 9 × 10⁹ × \(\frac { 1 }{ { \left( { 10 }^{ 2 } \right) }^{ 2 } } \) = 9 × 10³ N /C
But when intensity of electric field exceeds 3 × 10⁶ N / C air gets ionized and hence, electric discharge takes place. So l Cm of charge cannot be given to a sphere of radius 1 cm.

Question 4.
Two charge of one coulomb are separated by a distance of 1 meter from each other, find:

1. Force between the charge when was in air
2. If it is in dielectric medium, calculate its force.

Solution:
Given:
q₁= q₂ = 1 coulomb, r = l m

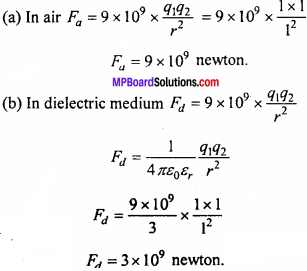
Question 5.
Two point charges + 9e and + e are placed 8 m apart. Where should the third charge q be placed on the line joining the two charges so that q should be in equilibrium?
Solution:
Let the charge q be placed at distance x from +9 e charge, then its distance from e will be 8 – x.
In equilibrium,


Taking + ve sign \(\frac { 3 }{ x }\) = \(\frac {1 }{ 8 – x}\)
⇒ 24 – 3x = x
24 = 4x or x = 6m
Taking – ve sign, \(\frac { 3 }{ x }\) = – \(\frac {1 }{ 8 – x}\)
⇒ 24 – 3x = -x
24 – 2x or x = 12 m
Since, +9e and+e are similar charges, hence q will be in equilibrium when x = 6 m i.e., q should be placed 6 m apart from +9e between the charges.

Question 6.
What is the force between two small sphere having charge of 2 × 10^-7 C and 3 × 10^-7C ? (NCERT)
Solution:
Given: q₁ = 2 × 10^-7C,
q₂ = 3 × 10^-7C,
and r = 30 cm = 30 × 10^-2
m = 0.3 m

The force will be repulsion force a both the charge are same.

Question 7.
The electrostatic force on a small sphere of charge 0.4µC due to another small sphere of charge 0.8µC in air is 2 N.

1. What is the distance between two sphere ?
2. What is the force on the second sphere due to the first ?

Solution:
Given:
q₁ = 0.4µC = 0.4 × 10^-6 C
q₂ = -0.8µC = -0.8 × 10^-6 C
F = 0.2N

= 9 × 2 × 8 × 10^-4
r = 3 × 4 × 10^-2
= 0.12 m = 12 cm.

(ii) Both the charges apply same force on each other. There force of first sphere due to second sphere will be 0.2 N. The force between them will be force of attraction.

Question 8.
A polythene piece is rubbed with woollen cloth as a result 3 x 10.7 coulomb charge is produced in it, then: .

1. How many electrons are transferred from which to which substance ?
2. Is mass transferred from woollen to polythene ?

Solution:

1. Polythene gets negative charge, so that electron is transferred from woollen to polythene.
We know that, q = ne

or n = 1.875 × 10¹² electrons.

2. As electrons are transferred from woolen to polythene, mass is also transferred in the same way.

Question 9.
A conductor has 14.4 × 10¹⁹ C positive charge. How many electrons are lacking or in excess ?
Solution:
We know that, q = ne
⇒ n =\(\frac { q }{ e}\)

Therefore, body is lacking by 9 electrons (as it has positive charge).

Question 10.
What is the net flux of uniform electric flux there through a cube of field oriented so that its faces are parallel to the coordinate plane ?
Solution:
All the faces of a cube are parallel to the coordinate axis. Therefore the Number of hold lines entering the cube is equal to the number of field lines piercing out of the cube. As a result net flux through the cube in zero.

MP Board Class 12th Physics Important Questions