MP Board Class 9th Maths Solutions Chapter 8 Quadrilaterals Ex 8.1
Question 1.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all Ijbe angles of the quadrilateral.
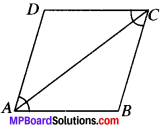
Solution:
∠A = 3x, ∠B = 5x, ∠C = 9x, ∠D = 13x
In quadrilateral ABCD
∠A + ∠B + ∠C + ∠D = 360°
(∴ Sum of all the angles of ♢ is equal to 360°)
3x + 5x + 9x + 13x = 360°
30x = 360°
x = \(\frac{360^{\circ}}{30^{\circ}}\)
Let angle in ratio be x then angles are x= 12°
∠A = 3 x 12° = 36°
∠B = 5 x 12° = 60°
∠C = 9 x 12° = 108°
∠D = 13 x 12° = 156°
Question 2.
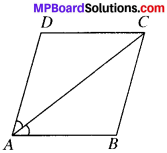
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Given
ABCD is a parallelogram in which
AC =DB
To prove:
ABCD is a rectangle.
Proof
In ∆DAB and ∆CBA
DB = CA (given)
AB = BA (common)
AD = BC (∴ opposites sides of ∥gm are equal)
∆DAB = ∆CBA (by SSS)
and so ∠DAB = ∠CBA
AD∥BC and AB is the transversal (by CPCT)
∴ ∠A + ∠B = 180° (CIA’s)
⇒ ∠A + ∠A = 180° (∴ ∠A = ∠B)
∴ ∠A = 90°
∠A = ∠C = 90°
and ∠B = ∠D = 90°
In ∥gm ABCD, all the angles are right angles.
ABCD is a rectangle.
![]()
Question 3.
Show that if the diagonals ofa quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Given
OA = OC, OB = OD and ∠AOD = 90°
To prove:
ABCD is a rhombus.
Proof:
In ∆AOD and ∆COB
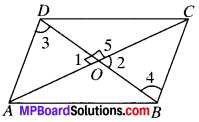
OA = OC (given)
OD = OB (given)
∠1 = ∠2 (V.O.A.’s)
∴ ∆AOD = ∆COB (by SAS)
and so AD = CB (by CPC 7)
∠3 = ∠4 (by CPCT)
∠3 and ∠4 are A.I.A.’s and are equal
∴ AD ∥ PC (proved)
AD = BC
∴ ABCD is a parallelogram
In ∆AOD and ∆COD,
OA = OC (given)
OD = OD (common)
∠1 = ∠5 = 90°
(∴ ∠1 + ∠5 = 180° ⇒ 90° + ∠5 = 180° ∴ ∠5 = 90°)
∴ ∠AOD = ∠COD (by SAS)
and so AD = CD (by CPCT)
In ∥gm APCD, all the sides are equal.
ABCD is rhombus.
Question 4.
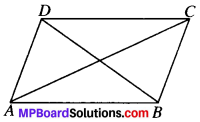
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given
ABCD is a square.
To prove:
- AC = BD
- OA = OC and OB = OD
- ∠AOD = 90°
Proof:
In ∆DAB and ACBA,
DA = CB (given)
AB = BA (common)
∠A = ∠B (each 90°)
∴ ∆DAB = ∆CBA (by SAS)
and so BD =AC (by CPCT)
2. In ∆AOD and ∆COB, AD = CB(given)
∠4 = ∠5 (A.I.A.’s)
∠6 = ∠7 (A.I.A. ’s)
∆AOD = ∆COB (by ASA)
and so OA=OC , (byCPCT)
OD = OB (byCPCT)
3. In ∆AOD and ∆COD,
AO = CO (proved)
OD = OD (common)
AD = CD (given)
∆AOD = ∆COD (by SSS)
and so ∠1 = ∠3 (byCPCT)
∠1 + ∠3 = 180° (LPA’S)
⇒ ∠1 + ∠1 = 180° (∠1 = ∠3)
⇒ 2∠1 = 180°
∴ ∠1 = \(\frac{180^{\circ}}{2}\)
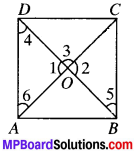
Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
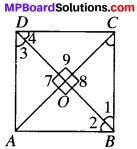
Give
ABCD is in which
AC = BD
OA = OC
and OB = OD
∠AOD = 90°
To prove
ABCD is a square
Proof:
In ∆AOD and ∆COB,
OA = OC (given)
OD = OB (given)
∠7 = ∠8 (V.CXA.’s)
∴ ∆AOD = ∠COB
and so AD = BC
and ∠3 = ∠1 (byCPCT)
∠3 and ∠1 are A.I.A.’s and are equal
∴ AD ∥ BC
Similarly, AB ∥ CD
∴ ABCD is a parallelogram.
In ∆AOD and ∆COD,
OA = OC (given)
OD = OD (common)
∠7 = ∠9 (each 90°)
∆AOD = ∠COD (by SAS)
AD = CD (byCPCT)
In ∥gmABCD, adjacent sidesAD = CD
∴ ABCD is a rhombus
In ∆DAB and ∆CBA,
DA = CB (proved)
AB = BA (common)
DB = CA (given)
∆DAB = ∆CBA (bySSS)
∠A = ∠B (by CPCT)
∠A + ∠B = 180° (CIA’s)
2∠A = 180°
∠A =90°
ABCD is a square.
![]()
Question 6.
Diagonals AC of a parallelogram ABCD bisects ∠A (see Fig). Show that
- it bisects ∠C also,
- ABCD is a rhombus.
Solution:
Given
ABCD is a parallelogram in which ∠1 = ∠2
To prove:
- ∠3 = ∠4
- ABCD is a rhombus.
Proof
1. ∠1 = ∠4 (A.I.A.’s) ….(i)
(∴ AD ∥ SC and AC is the transversal)
∠2 = ∠3 (A.I.A.’s) …(ii)
(∴ AB ∥ DC and AC is the transversal)
∠1 = ∠2 (given) …(iii)
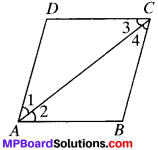
From (i), (ii) and (iii), we get
∠4 = ∠3
(ii) From (ii) and (iii), we get,
∠1 = ∠3
In ∆ADC,
∠1 = ∠3
∴ AD = DC (In a A, sides opposites to equal angles are equal) and so ABCD is a rhombus
(∴ In a ∥gm, if adjacent sides are equal then it is a rhombus)
Question 7.
ABCD is a rhombus, show that diagonal AC biusects ∠A as well as ∠C and diagonal BD biusects ∠B as well as ∠D.
Solution:
Given
ABCD is a rhombus.
To prove
∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8.
Proof:
In ∆ADC and ∆ABC.
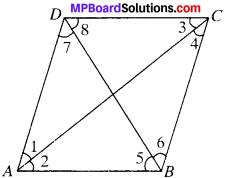
AD = AB (Adj. sides of a rhombus)
DC = BC (Adj. sides of a rhombus)
AC = AC (common)
∴ ∆ADC = ∆ABC (by SSS)
so ∠1 = ∠2 (by CPCT)
and ∠3 = ∠4 (by CPCT)
∴ AC bisects ∠A and ∠C
Similarly, ∠5 = ∠6 and ∠7 = ∠8
BD bisects ∠B and ∠D.
Question 8.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
Solution:
Given
ABCD is a rectangle.
∠1 = ∠2 and ∠3 = ∠4
To prove:
- ABCD is a square
- ∠5 = ∠6 and ∠7 = ∠8
Proof:
1. ∠A = ∠C
(∵ Rectangle is ∥gm and in a ∥gm opp. angles are equal.)
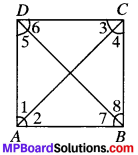
\(\frac{1}{2}\)∠A = \(\frac{1}{2}\)∠C
∠A = ∠C
∠2 = ∠4
In ∆ABC, ∠2 = ∠4
AB = BC
(In a A, sides opp. to equal angles are always equal)
ABCD is a rectangle in which adjacent sides are equal.
∴ ABCD is a square.
2. In ∆ABD,
AB = AD (∴ ABCD is a square)
∴ ∠5 = ∠7 (∴ In a A, angles opp. to equal sides are equal) ….(1)
AB ∥ DC and BD is the transversal
∴ ∠6 = ∠7 …(2)
AD ∥ BC and BD is the transversal.
∴ ∠5 = ∠8 …(3)
From (1) and (3), we get
∠7 = ∠8
From (1) and (2), we get
∠5 = ∠6
Diagonal BD bisects ∠B as well as ∠D.
Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig.). Show that
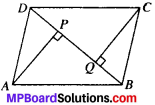
- ∆APD = ∆CQB
- AP = CQ
- ∆AQB = ∆CPD
- AQ = CP A
- APCQ is a parallelogram
Given
ABCD is a parallelogram.
∴ AD = BC, AB= DC and DP = BQ
To prove:
- ∆APD = ∆CQB
- AP = CQ
- ∆AQB = ∆CPD
- AQ = CP
- APCQ is a parallelogram
Proof:
In ∆APD and ∆CQB
PD = QB (given)
AD = CB (given)
∠2 = ∠1 (AIA’s)
∆APD = ∆CQB (by SAS)
and so AP = CQ (by CPCT)
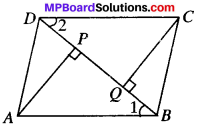
In ∆AQB and ∆CPD,
AB = CD (given)
∠3 = ∠4 (AIA’s)
BQ = DP (given)
∆AQB = ∆CPD (by SAS)
and so AQ = CP (by CPCT)
In quadrilaterals AQCP,
AP = CQ
AQ = CP
AQCP is a parallelogram.
![]()
Question 10.
ABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal BD (see Fig.). Show that
- ∆APB = ∆CQD
- AP = CQ
Solution:
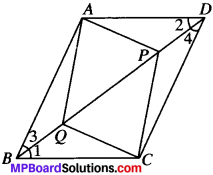
Given
ABCD is a ∥gm in which Ap ⊥ BD and CQ ⊥ BD.
To prove:
- ∆APB = ∆CQD
- AP = CQ
Proof:
In ∆APB and ∆CQD,
∠P = ∠Q (each 90°)
∠1 = ∠2 (AIA’s)
AB = CD (given)
∆APB ≅ ∆CQD (byAAS)
and so AP = CQ (by CPCT)
Question 11.
In ∆ABC and ∆DEF, AB = DE, AB ∥ DE, BC = EF and BC ∥ EE. Vertices A, B and C are joined to vertices, D,E and F respectively (see Fig.). Show that
- quadrilateral ABED is a parallelogram
- quadrilateral BEFC is a parallelogram
- AD ∥ CF and AD = CF
- quadrilateral ACFD is a parallelogram
- AC = DF
- ∆ABC = ∆DEF.
Solution:
Given
AB = DE and AB ∥ DE
BC = EF and BC ∥ EF
To prove
- ABED is a ∥gm
- BEFC is a ∥gm
- AD ∥ CF and AD – CF
- ACFD is a ∥gm
- AC =DF
- ∆ABC ≅ ∆DEF
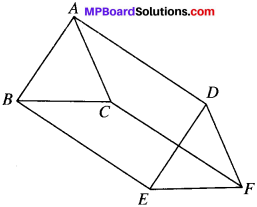
Proof:
1. AB = DE and AB ∥ DE (given)
ABED is ∥gm
and so AD ∥ BE and AD = BE …(1)
2. BC = EF and BC ∥ FC (given)
BEFC is a ∥gm
and so BE ∥ CF and BE = CF …..(2)
3. From (1) and (2), we get
AD ∥ CF and AD = CF
4. AD ∥ CF and AD = CF (proved)
ACFD is a ∥gm
5. and so AC = DF
(In a parallelogram, opp. sides are equal)
6. In ∆ABC and ∆DEF,
AB = DE (given)
BC = EF (given)
AC = DF (proved)
∆ABC = ∆DEF (by SSS)
![]()
Question 12.
ABCD is a trapezium in which AB ∥ CD and AD = BC (see Fig.). Show that:
- ∠A = ∠B
- ∠C = ∠D
- ∆ABC ≅ ∆BAD
- Diagonal AC = diagonal BF)
[Hint: Extend AB and draw line through C parallel to DA intersecting AB produced at E.]
Solution:
Given
AB ∥ CD, AD = BC
To prove:
- ∠A = ∠B
- ∠C = ∠D
- ∆ABC ≅ ∆BAD
- diagonal AC = diagonal BD
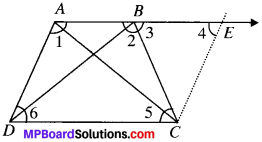
Construction:
Draw a line CE ∥ DA which intersect AB produced at E.
Proof:
1. In quadrilateral ADCE,
AD ∥ EC (by const)
and AE ∥ DC ( AB ∥ DC)
∴ ADCE is a parallelogram
and so AD = EC (opp. sides of a ∥ are equal)…(i)
AD = BC (given) ….(ii)
From (i) and (ii), we get
BC = EC
In ∆BCE BC = EC (proved)
∠4 = ∠3
(∴ In a ∆, angles opp. to equal sides are equal)
∠2 + ∠3 = 180° (LPA’s) …(iii)
∠1 + ∠4 = 180° (CIA’s) …(iv)
From (iii) and (iv), we get
∠2 + ∠3 = ∠1 + ∠4
∠2 = ∠1 (∠3 = ∠4)
i.e., ∠A = ∠B
2. ∠3 = ∠5 (AIA’s) …(v)
∠6 = ∠4
(∴ ADCE is a ∥gm and in a ∥gm opp. angles are equal) …(vi)
∠4 = ∠3 (proved) …(vii)
From (v), (vi) and (vii), we get
∠5 = ∠6
i.e., ∠C = ∠D
3. In ∆ABC and ∆BAD,
AB = BA (common)
BC = AD (given)
∠2 = ∠1 (proved)
∆ABC ≅ ∆BAD (by SAS)
and so AC =BD (by CPCT)
4. diagonal AC = diagonal BD (proved)
![]()
Mid Point Theorem:
The line segment joining the mid-points of the sides of a triangle is parallel to the third side and equal to half of it.
Given.
ABC is a A in which D and E are the mid-points of sides AB and AC respectively.
To prove.
DE ∥ BC and DE = \(\frac{1}{2}\) BC
Construction:
Extend DE uptoFsuch that DE = EF. Join CF.
Proof:
In ∆AED and ∆CEE
AE = CE (E is the mid – point of AC)
∠AED = ∠CEF (VOA’s)
DE = FE (By constriction)
∆AED = ∆CEF , (By SAS)
and so ∠DAE = ∠FCE (By CPCT)
AD = CF (By CPCT)
∠DAE and ∠FCE are alternate interior angles and are equal.
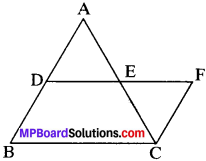
AD ∥ FC
⇒ DB ∥ FC
Now, AD = DB and AD = FC
DB = FC
In BCFD, DB ∥ FC and DF = BC
BCFD is a ∥gm
and so DF ∥ BC and DF = BC
⇒ DF ∥ BC and 2DF = BC
DE ∥ BC and DE = \(\frac{1}{2}\) BC
Converse of mid point theorem:
The line drawn through the mid – point of one side of a triangle and parallel to another side, bisects the third side.
Given
ABC is a A in which D is the mid-point of AB and DE ∥ BC.
To Prove:
E is the mid – point of AC.
Construction:
Mark a point F on AC and join DF.
Proof:
Let E be not the mid – point of AC. Let us assume that F be the mid – point of AC.
Then by mid-point theorem
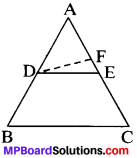
DF ∥ BC
DE ∥ BC (Given)
From (i) and (ii), we get
DE ∥ DF
But lines DE and DF are intersecting lines, intersecting at D. This is a contradiction. So our supposition is wrong. Hence E is the mid – point of AC.