MP Board Class 9th Maths Solutions Chapter 7 त्रिभुज Ex 7.4
प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है। (2018)
हल:
ज्ञात है ∆ABC का कोण B समकोण है।
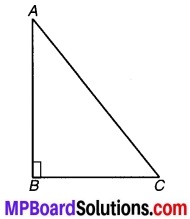
चित्र 7.20
चूँकि ∠B > ∠C तथा ∠B > ∠A (त्रिभुज में समकोण सबसे बड़ा होता है)
⇒ AC > AB तथा AC > BC (बड़े कोण की सम्मुख भुजा बड़ी होती है)
अतः समकोण त्रिभुज में कर्ण सबसे बड़ा होता है। इति सिद्धम् ।
प्रश्न 2.
संलग्न चित्र में ∆ABC की भुजाएँ AB और AC को क्रमशः बिन्दुओं Pऔर ए तक बढ़ाया गया है। साथ ही ∠PBC < ∠QCB है। दर्शाइए कि AC > AB है।
हल:
चूँकि ∠PBC < ∠QCB (दिया है)
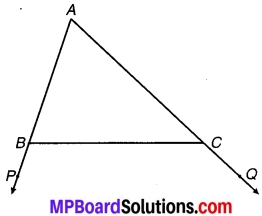
चित्र 7.21
⇒ ABC > ∠ACB (छोटे कोण का सम्पूरक बड़े कोण के सम्पूरक से बड़ा होता है)
अतः AC > AB. (त्रिभुज से बड़े कोण के सामने की भुजा बड़ी होती है) इति सिद्धम्
प्रश्न 3.
संलग्न चित्र में ∠ B < ∠A और ∠C < ∠D BN है। दर्शाइए कि-
AD < BC है।

चित्र 7.22
हल:
चूँकि ∆OAB में, ∠B < ∠A (दिया है)
⇒ AO < BO …(1) AD (∆ में छोटे कोण के सामने की भुजा छोटी होती है)
चूँकि ∆OCD में, ∠C < ∠D (दिया है)
⇒ OD ⇒ AO + OD < BO + OC – [समीकरण (1) और (2) से]
अतः AD < BC. (∵ AO + OD = AD एवं BO + OC = BC) इति सिद्धम् प्रश्न 4. AB और CD क्रमशः एक चतुर्भुज की सबसे छोटी और सबसे बड़ी भुजाएँ हैं (देखिए संलग्न चित्र)। दर्शाइए कि- ∠A >∠C और ∠B >∠D है।
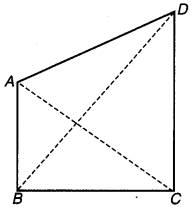
चित्र 7.23
हल:
प्रश्नानुसार, AB < BC, AB < CD एवं AB < AD तथा CD > AB, CD > BC एवं CD > AD.
AC और BD को मिलाइए।
चूँकि ∆ABC में, BC > AB (∵ AB < BC दिया है) ⇒ ∠BAC > ∠BCA, (बड़ी भुजा के सामने का कोण) …(1)
तथा ∆ACD में, CD > AD (दिया है)
⇒ ∠CAD > ∠ACD (बड़ी भुजा के सामने का कोण) …(2)
⇒ ∠BAC + ∠CAD > ∠BCA + ∠ACD [समी. (1) और (2) से]
अतः ∠A > ∠C. इति सिद्धम् चूँकि
चूँकि ∆ABD में, AD > AB (दिया है)
⇒ ∠ABD > ∠ADB . (बड़ी भुजा का सम्मुख कोण) …(1)
तथा ∆BCD में, CD > BC (दिया है)
⇒ ∠DBC > ∠BDC (बड़ी भुजा का सम्मुख कोण) …(2)
⇒ ∠ABD + ∠DBC > ∠ADB+ ∠BDC [समी. (1) और (2) से]
अतः ∠B >∠D. इति सिद्धम्
![]()
प्रश्न 5.
संलग्न चित्र में PR> PQ और PS कोण DPR को समद्विभाजित करता है।
सिद्ध कीजिए कि – ∠PSR> ∠PSQ.
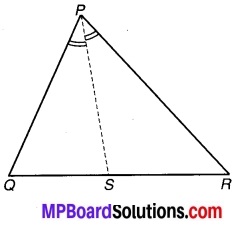
चित्र 7.24
हल:
चूँकि ∆POR में, PR > PQ
⇒ ∠Q >∠R (बड़ी भुजा का सम्मुख कोण) …(1)
दिया है : ∠OPS = ∠SPR (PS ∠QPR का समद्विभाजक दिया है) …(2)
अब ∠QPS + ∠Q+ ∠PSQ = ∠SPR + ∠R + ∠PSR = 180°
(त्रिभुज के अन्त:कोणों का योग) ∠Q+ ∠PSQ = ∠R + ∠PSR [∵ ∠QPS = ∠SPR, समी. (2) से]
लेकिन ∠Q > ∠R [समीकरण (1) से]
⇒ ∠PSQ < ∠PSR अतः ∠PSR > ∠PSQ. इति सिद्धम्
प्रश्न 6.
दर्शाइए कि एक रेखा पर एक दिए हुए बिन्दु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखण्ड खींचे जा सकते हैं, उनमें लम्ब रेखाखण्ड सबसे छोटा होता है।
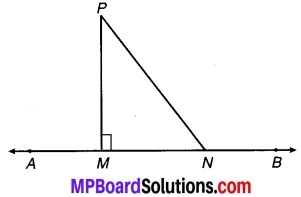
चित्र 7.25
हल:
ज्ञात है : रेखा AB के बाहर कोई बिन्दु P है। P से PM ⊥ AB खींचा गया है। AB पर एक अन्य कोई बिन्दु N है तथा PN को मिलाया गया है।
अब ∆PMN में, ∠PMN = 90°
⇒ ∠PMN > ∠PNM (समकोण A में समकोण सबसे बड़ा होता है)
⇒ PN > PM (बड़े कोण की सम्मुख भुजा बड़ी होती है)
⇒ PM < PN.
चूँकि रेखा पर N कोई या ऐच्छिक बिन्दु है।
अतः रेखा के बाहर किसी बिन्दु से रेखा पर जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब सबसे छोटा होता है। इति सिद्धम्