MP Board Class 9th Maths Solutions Chapter 10 वृत्त Ex 10.2
प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हैं। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करती हैं। (2018, 19)
हल:
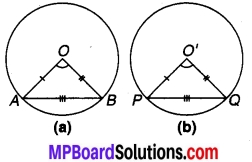
चित्र 10.1
दिया है : दो सर्वांगसम वृत्त जिनके केन्द्र O तथा O’ हैं।
जीवा AB = जीवा PQ केन्द्रों पर ∠AOB और ∠PO’Q अन्तरित करते हैं।
अब ΔOAB और OPQ में,
चूँकि OA = O’P (सर्वांगसम वृत्तों की त्रिज्याएँ हैं)
OB = O’Q (सर्वांगसम वृत्तों की त्रिज्याएँ हैं)
AB = PQ (दिया है)
⇒ ΔΟΑΒ ≅ ΔΟΡΟ (SSS सर्वांगसम प्रमेय)
⇒ ∠AOB = ∠PO’Q (CPCT)
अतः सर्वांगसम वृत्तों की बराबर जीवाएँ केन्द्रों पर बराबर कोण अन्तरित करती हैं। इति सिद्धम्
![]()
प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करें, तो जीवाएँ बराबर होती हैं।
हल:
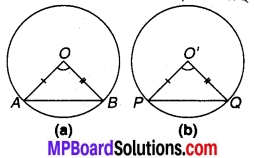
चित्र 10.2
दिया है : दो सर्वांगसम वृत्त जिनके केन्द्र O तथा O’ है तथा जीवाएँ AB और PQ केन्द्रों पर क्रमशः
∠AOB = ∠PO’Q अन्तरित करती हैं।
अब ΔAOB और ΔPO’Q में,
चूँकि OA = O’P (सर्वांगसम वृत्तों की त्रिज्याएँ हैं)
∠AOB = ∠PO’Q (दिया है)
OB = O’Q (सर्वांगसम वृत्तों की त्रिज्याएँ)
⇒ ΔAOB ≅ ΔPO’Q (SAS सर्वांगसमता प्रमेय)
⇒ AB = PQ (CPCT)
अतः सर्वांगसम वृत्तों में वे जीवाएँ जो केन्द्र पर बराबर कोण अन्तरित करती हैं आपस में बराबर होती हैं। इति सिद्धम्