MP Board Class 8th Maths Solutions Chapter 7 घन और घनमूल Ex 7.2

प्रश्न 1.
अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित में से प्रत्येक संख्या का घनमूल ज्ञात कीजिए –

64
512
10648
27000
15625
13824
110592
46656
175616
91125

हल:
1.
MP Board Class 8th Maths Solutions Chapter 7 घन और घनमूल Ex 7.2 img-1
2.

3.

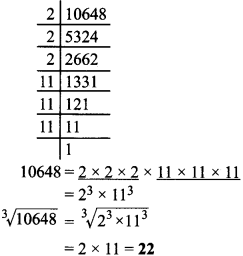
4.

5.

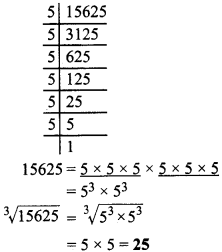
6.

7.

8.

9.

10.

प्रश्न 2.
बताइए सत्य है या असत्य –

किसी भी विषम संख्या का घन सम होता है।
एक पूर्ण घन दो शून्यों पर समाप्त नहीं होता है।
यदि किसी संख्या का वर्ग 5 पर समाप्त होता है, तो उसका घन 25 पर समाप्त होता है।
ऐसा कोई पूर्ण घन नहीं है जो 8 पर समाप्त होता है।
दो अंकों की संख्या का घन तीन अंकों वाली संख्या हो सकती है।
दो अंकों की संख्या के घन में सात या अधिक अंक हो सकते हैं।
एक अंक वाली संख्या का घन एक अंक वाली संख्या हो सकती है।

उत्तर:

असत्य
सत्य
असत्य
असत्य
असत्य
असत्य
सत्य।

प्रश्न 3.
आपको यह बताया जाता है कि 1331 एक पूर्ण घन है। क्या बिना गुणनखण्ड किए आप यह अनुमान लगा सकते हैं कि इसका घनमूल क्या है? इसी प्रकार 4913, 12167 और 32768 के घनमूलों के अनुमान लगाइए।
हल:
1331 के लिए इस संख्या के दो समूह 1 और 331 हैं।
331 का इकाई अंक 1 है। अतः घनमूल का इकाई अंक 1 होगा।
दूसरे समूह का अंक 1 है।
∴ 1³ = 1, अतः घनमूल का दहाई का अंक 1 होगा।
\(\sqrt[3]{1331}\) = 11
4913 के लिए
4913 के दो समूह बनाए 4 और 913
प्रथम समूह 913 का इकाई अंक 3 है। 3 किसी संख्या के स्थान पर तब आता है जब उसके घनमूल के इकाई का अंक 7 हो।
अतः घनमूल का इकाई अंक = 7
दूसरे समूह 4 के लिए
1³ = 1 और 2³ = 8
अतः 1³ < 4 < 2³
अतः घनमूल का दहाई अंक = 1
∴ \(\sqrt[3]{4913}\) = 17
12167 के लिए
12167 के दो समूह बनाए 12 और 167
प्रथम समूह 167 में इकाई का अंक 7 है, 7 पर समाप्त होने वाली संख्या का घनमूल = 3
अतः घनमूल का इकाई अंक = 3.
दूसरे समूह 12 के लिए
23 = 8 और 33 = 27
2³ < 12 < 3³ अतः घनमूल का दहाई का अंक = 2
∴ \(\sqrt[3]{12167}\) = 23
32768 के लिए
संख्या का प्रथम समूह 768 तथा दूसरा समूह 32.
प्रथम समूह की संख्या का इकाई अंक 8 है। 8 किसी संख्या के स्थान पर तब आता है जब उसके घनमूल का इकाई अंक 2 हो।
अतः घनमूल का इकाई अंक = 2
दूसरे समूह 32 के लिए
3³ = 27 और 4³ = 64
इसलिए 3³ < 32 < 4³ अतः घनमूल का दहाई का अंक = 3
∴ \(\sqrt[3]{32768}\) = 32