MP Board Class 8th Maths Solutions Chapter 7 Cube and Cube Roots Ex 7.2
Question 1.
Find the cube root of each of the following numbers by prime factorisation method.
(i) 64
(ii) 512
(iii) 10648
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution:


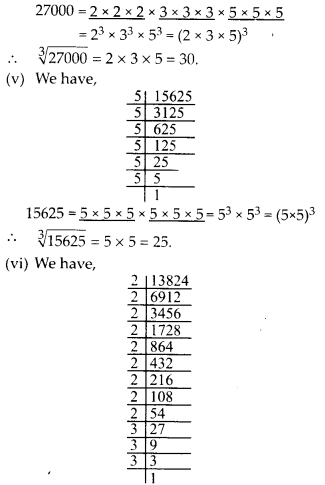
![]()
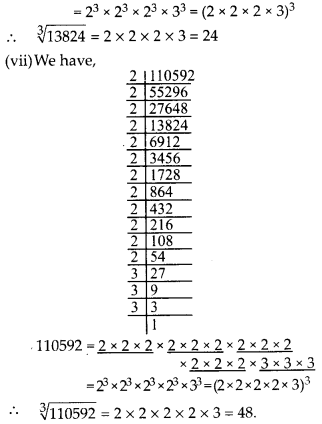
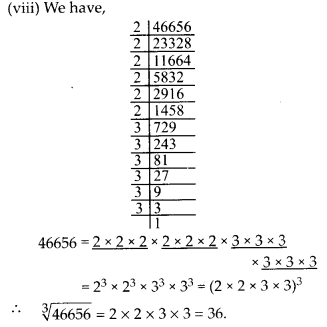


![]()
Question 2.
State true or false.
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution:
(i) False
Because the cube of any odd number is odd.
(ii) True
Because to make a perfect cube, we need each and every factor to occur three times in a group.
So, we need 3, 6, 9, …. zeros to make a perfect cube.
(iii) False
152 = 225, which ends with 5.
and 153 = 3375, which ends with 75.
(iv) False
∵ 123 = 1728, which ends with 8.
(v) False
∵ 103 = 1000, where 10 is the smallest two digit number, and its cube contains 4 digits.
(vi) False
∵ 993 = 970299, where 99 is the largest two digit number and its cube contains 6 digits.
(vii) True
∵ 13 = 1, Which is a single digit number.
![]()
Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution:
The given number is 1331.
Step-1: Start making groups of three digits starting from the right most digit of the, number we get 331 and 1 as two groups of three and one digits.
Step-2: First group, i.e., 331 will give the one’s digit (unit’s) of the required cube root. The number 331 ends with 1. We know that 1 comes at the unit’s place of a number only
when its cube root ends in 1.
So, we get 1 at the unit’s place of the cube root.
Step-3: Now take another group, i.e., 1
We know that 13 = 1 and 23 = 8. Also 1 ≤ 1 ≤ 8. We take the smaller number 1 as the ten’s place of the required cube root. So, we get
\(\sqrt[3]{1331}=11\)
Cube root of 4913
Step-1: Forming groups of three digits starting ’ from the right most digit of 4913 we get two groups 913 and 4.
Step-2: One’s place digit of first group is 3.
∴ We take one’s place digit of required cube root is 7(∵ 73 = 343)
Step-3: Now the second group is 4.
13 = 1, 23 = 8
1 < 4 < 8, hence 1 is the ten’s place digit of required cube root.
So, we get \(\sqrt[3]{4913}\) = 17.
Cube root of 12167.
Step-1 : Forming groups of three digits starting from the right most digit of 12167 we get two groups 167 and 12.
Step-2 : First group is 167.
∴ unit’s place digit of required cube root is 3. (∵ 33 = 27)
Step-3: Second group is 12
23 = 8 and 33 = 27, 8 < 12 < 27
⇒ 23 < 12 < 33
∴ 2 is the ten’s place digit of required cube root. So, we get \(\sqrt[3]{12167}\) = 23.
Cube root of 32768
Step-1: Forming groups of three digits starting from the right most digit of 32768 we get two groups 768 and 32.
Step-2: First group is 768.
∴ unit’s place digit of required cube root is 2
(∵ 23 = 8).
Step-3: Second group is 32
33 = 27 and 43 = 64, 27 < 32 < 64
⇒ 33 < 32 < 43
∴ 3 is the ten’s place digit of required cube root. So, we get \(\sqrt[3]{32768}\) = 32.