In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 Matrices Ex 3.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Solutions Chapter 3 Matrices Ex 3.1
![]()
Question 1.
In the matrix A = \(\left[\begin{array}{cccc} 2 & 5 & 19 & -7 \\ 35 & -2 & \frac{5}{2} & 12 \\ \sqrt{3} & 1 & -5 & 17 \end{array}\right]\), write
i. the order of the matrix,
ii. the number of elements.
iii. Write the elements a13, a21, a33, a24, a23.
Solution:
i. The matrix has 3 rows and 4 columns. Hence the order of A is 3 x 4
ii. Number of elements = 3(4) = 12
iii. a13 = 19,
a21 = 35,
a33 = – 5,
a24 = 12,
a23 = \(\frac { 5 }{ 2 }\)
![]()
Question 2.
If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
Solution:
The ordered pairs of natural numbers whose product is 24 are (1, 24), (2, 12), (3, 8), (4, 6), (6,4), (8,3), (12,2) and (24,1). Hence the possible orders are 1 X 24, 2 x 12, 3 x 3, 8, 4 x 6, 6 x 4, 8 x 3, 12 x 2, 24 x 1.
The possible orders with 13 elements are 1 x 13, 13 x 1
Question 3.
If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Solution:
The ordered pairs of natural numbers whose product is 18 are (1, 18), (2, 9), (3, 6), (6, 3), (9, 2) and (18, 1).
Hence the possible orders are 1 x 18, 2 x 9, 3 x 6, 6 x 3, 9 x 2, 1.8 x 1
The possible orders with 5 elements are 1 x 5, 5 x 1.
Question 4.
Construct a 2 x 2 matrix, A = [aij], whose elements are given by
i. aij = \(\frac{(i+j)^{2}}{2}\)
ii. aij = \(\frac{i}{j}\)
iii. aij = \(\frac{(i+2j)^{2}}{2}\)
Solution:
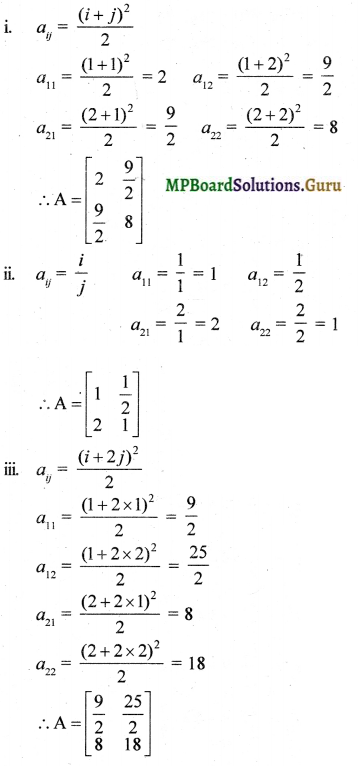
![]()
Question 5.
Construct a 3 x 4 matrix, whose elements are given by
i. aij = \(\frac{1}{2}\)|-3i + j|
i. aij = 2i – j
Solution:
The general form of a 3 x 4 matrix is
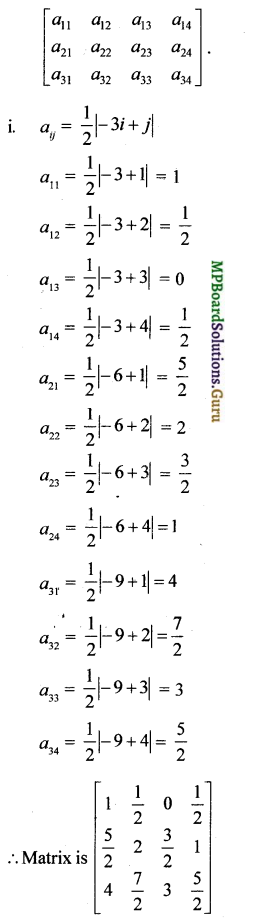
ii. The general form of a 3 x 4 matrix is

![]()
Question 6.
Find the values of x, y and z from the following equations:
i. \(\left[\begin{array}{ll}
4 & 3 \\
x & 5
\end{array}\right]=\left[\begin{array}{ll}
y & z \\
1 & 5
\end{array}\right]\)
ii. \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{cc}
6 & 2 \\
5 & 8
\end{array}\right]\)
iii. \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
Solution:
i. \(\left[\begin{array}{ll}
4 & 3 \\
x & 5
\end{array}\right]=\left[\begin{array}{ll}
y & z \\
1 & 5
\end{array}\right]\)
Comparing the corresponding elements of the two matrices, we get x = 1, y = 4, z = 3.
ii. \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{cc}
6 & 2 \\
5 & 8
\end{array}\right]\)
Equating the corresponding elements, we get
x + y = 6, 5 + z = 5, xy = 8
Solving we get x = 2, y = 4, z = 0
or x = 4, y = 2, z = 0
iii. \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
⇒ x + y + z = 9 … (1)
x + z = 5 … (2)
y + z = 7 … (3)
(2) + (3) ⇒ x + y + 2z = 12
(1) ⇒ x + y + z = 9
Subtracting we get z = 3
∴ x = 2,y = 4, z = 3
![]()
Question 7.
Find the value of a, b, c and d from the equation:
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
Solution:
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
Equating the corresponding elements of the two matrices, we get
a – b = – 1 ………… (1)
2a + c = 5 ……….. (2)
2a – b = 0 ……….. (3)
3c + d = 13 ……….. (4)
(3) – (1) ⇒ a = 1
(3) ⇒ b = 2
(2) ⇒ c = 3
(4) ⇒ d = 4
Question 8.
A = [a]m x n is a square matrix, if
(a) m n
(c) m = n
(d) None of these
Solution:
(c) m = n
For a square matrix
Number of rows = Number of columns
∴ m = n
![]()
Question 9.
Which of the given values of x and y make the following pair of matrices equal?
\(\left[\begin{array}{cc}
3 x+7 & 5 \\
y+1 & 2-3 x
\end{array}\right],\left[\begin{array}{cc}
0 & y-2 \\
8 & 4
\end{array}\right]\)
(a) x= \(\frac { -1 }{ 3 }\), y = 7
(b) Not possible to find
(c) y = 7, x = \(\frac { -2 }{ 3 }\)
(d) x = \(\frac { -1 }{ 3 }\), y = \(\frac { – 2 }{ 3 }\)
Solution:
(b) For equal matrices, the corresponding elements are equal. Equating the corre-spondingelements, we get x = \(\frac { -7 }{ 3 }\), y = 7, y = 7 and x = \(\frac { -2 }{ 3 }\)
x has 2 values which is not possible.
Question 10.
The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is:
(a) 27
(b) 18
(c) 81
(d) 512
Solution:
(d) 512
There are 9 elements and each element can be either 0 or 1.
The 9 places can be filled in 29 ways.
∴ Total number of ways = 29 = 512