In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Solutions Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise
![]()
Question 1.
cos-1(cos\(\frac { 13π }{ 6 }\))
Solution:
The principal value brach of cos-1 is [0, p]

Question 2.
tan-1(tan\(\frac { 7π }{ 6 }\))
Solution:
The principal value brach of tan-1 is (- \(\frac { π }{ 2 }\), \(\frac { π }{ 2 }\))

![]()
Question 3.
2sin-1\(\frac { 3 }{ 5 }\) = tan-1\(\frac { 24 }{ 7 }\)
Solution:
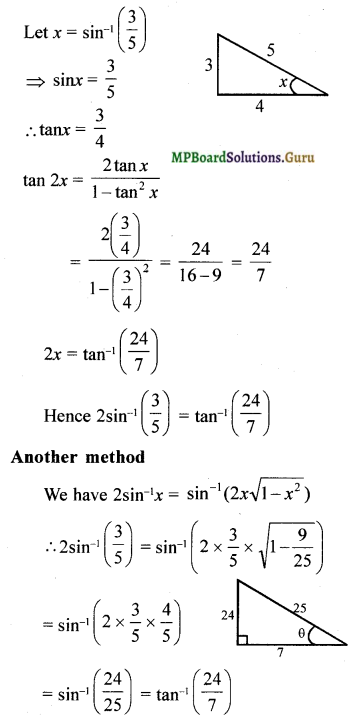
Question 4.
sin-1\(\frac { 8 }{ 17 }\) + sin-1\(\frac { 3 }{ 5 }\) = tan-1\(\frac { 77 }{ 36 }\)
Solution:

Question 5.
cos-1\(\frac { 4 }{ 5 }\) + cos-1\(\frac { 12 }{ 13 }\) = cos-1\(\frac { 33 }{ 65 }\)
Solution:

![]()
Question 6.
cos-1\(\frac { 12 }{ 13 }\) + sin-1\(\frac { 3 }{ 5 }\) = sin-1\(\frac { 56 }{ 65 }\)
Solution:
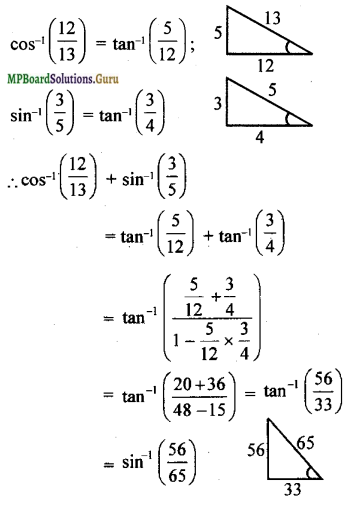
Question 7.
tan-1\(\frac { 63 }{ 16 }\) = sin-1\(\frac { 5 }{ 13 }\) + cos-1\(\frac { 3 }{ 5 }\)
Solution:
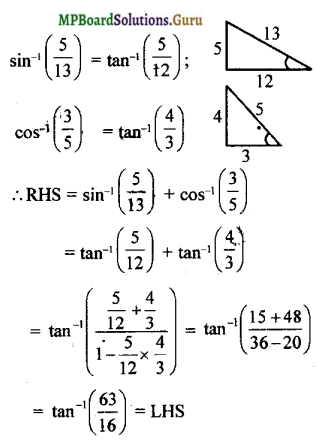
Question 8.
tan-1\(\frac { 1 }{ 5 }\) + tan-1\(\frac { 1 }{ 7 }\) + tan-1\(\frac { 1 }{ 3 }\) + tan-1\(\frac { 1 }{ 8 }\) = \(\frac { π }{ 4 }\)
Solution:
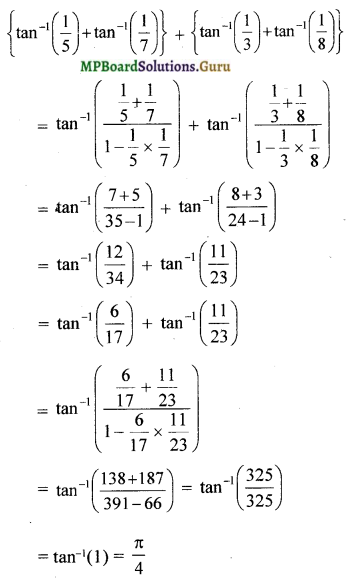
![]()
Question 9.
tan-1\(\sqrt{x}\) = \(\frac { 1 }{ 2 }\)cos-1\(\left(\frac{1-x}{1+x}\right), x \in[0,1]\)
Solution:
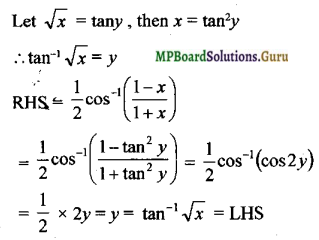
Question 10.
cot-1\(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\) = \(\frac { x }{ 2 }\) x ∈ (0, \(\frac { π }{ 4 }\))
Solution:
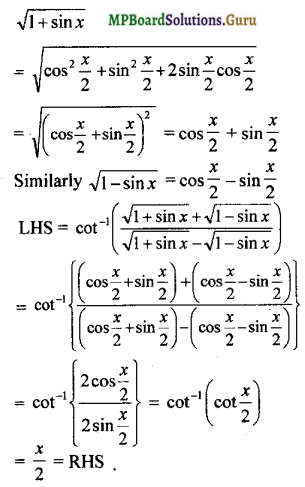
Question 11.
tan-1\(\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right)\) = \(\frac { π }{ 4 }\) – \(\frac { 1 }{ 2 }\) cos-1 x, – \(\frac{1}{\sqrt{2}} \leq x \leq 1\)
Solution:

![]()
Question 12.
\(\frac { 9p }{ 8 }\) – \(\frac { 9 }{ 4 }\)sin-1\(\frac { 1 }{ 3 }\) = \(\frac { 9 }{ 4 }\)sin-1\(\frac{2 \sqrt{2}}{3}\)
Solution:

Question 13.
2tan-1(cosx) = tan-1(2cosecx)
Solution:

Question 14.
tan-1\(\frac{1-x}{1+x}\) = \(\frac { 1 }{ 2 }\) tan-1x, (x > 0)
Solution:

![]()
Question 15.
sin(tan-1x), |x| < 1 is equal to
a. \(\frac{x}{\sqrt{1-x^{2}}}\)
b. \(\frac{1}{\sqrt{1-x^{2}}}\)
c. \(\frac{1}{\sqrt{1+x^{2}}}\)
d. \(\frac{x}{\sqrt{1+x^{2}}}\)
Solution:
d. \(\frac{x}{\sqrt{1+x^{2}}}\)

Question 16.
sin-1(1 – x) – 2sin-1x = \(\frac { π }{ 2 }\), then x is equal to
a. 0, \(\frac { 1 }{ 2 }\)
b. 1, \(\frac { 1 }{ 2 }\)
c. 0
d. \(\frac { 1 }{ 2 }\)
Solution:
c. 0

But x ≠ \(\frac { 1 }{ 2 }\), since sin-1(1 – \(\frac { 1 }{ 2 }\)) ≠ \(\frac { π }{ 2 }\) + 2 sin-1\(\frac { 1 }{ 2 }\)
∴ x = 0.
![]()
Question 17.
tan-1 \(\frac { x }{ y }\) – tan-1 \(\frac{x-y}{x+y}\)
Solution:
a. \(\frac { π }{ 2 }\)
b. \(\frac { π }{ 3 }\)
c. \(\frac { π }{ 4 }\)
d. \(\frac { -3π }{ 4 }\)
Solution:
c. \(\frac { π }{ 4 }\)
