MP Board Class 12th Maths Book Solutions Chapter 11 प्रायिकता विविध प्रश्नावली

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 11 प्रायिकता विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 11 प्रायिकता विविध प्रश्नावली

प्रश्न 1.
दिखाइए कि मूल बिन्दु से (2, 1, 1) मिलाने वाली रेखा, बिन्दुओं (3, 5, -1 ) और (4, 3, – 1)से निर्धारित रेखा पर लम्ब है।
हल:
बिन्दु A(2, 1, 1) और मूल बिन्दु B (0, 0, 0) से जाने वाली रेखा AB के दिक्-अनुपात 2 – 0, 1 – 0 या 2, 1, 1
बिन्दु C (3, 5, – 1) और D (4, 3, – 1) से निर्धारित रेखा के दिक्-अनुपात 4 – 3, 3 – 5, – 1 + 1 या 1, – 2, 0 हैं।
AB और CD लम्ब हैं यदि
a₁a₂ + b₁b₂+ c₁c₂ = 0
अब a₁a₂ + b₁b₂+ c₁c₂
= 2 x 1 + 1 x (- 2) + 1 x 0
= 2 – 2 + 0 = 0
अतः AB और CD परस्पर लम्ब हैं।

प्रश्न 2.
यदि दो परस्पर लम्ब रेखाओं की दिक्-कोसाइन l₁, m₁, n₁, और l₂, m₂, n₂ हों तो दिखाइए कि इन दोनों पर
लम्ब रेखा की दिक्-कोसाइन m₁n₂ – m₂n₁ – n₁l₂ – n₂l₁, l₁m₂ – l₂m₁ हैं।
हल:
माना दो रेखाएँ AB और CD जिसकी दिक्-कोसाइन क्रमश: l₁, m₁, n₁ और l₂, m₂, n₂ हैं
जो परस्पर लम्ब हैं।
l₁l₂ + m₁m₂ + n₁n₂ = 0
l₁, m₁, n₁ और l₂, m₂, n₂ दिक्-कोसाइन है तो

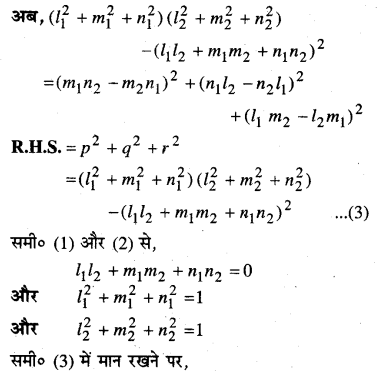
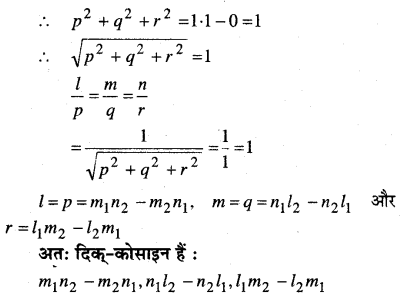
प्रश्न 3.
उन रेखाओं के मध्य का कोण ज्ञात कीजिए जिनके दिक् अनुपात a, b, c और b – c, c – a, a – b हैं।
हल:
माना रेखाओं के मध्य का कोण θ है तब
cos θ = \(\frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^{2}+b^{2}+c^{2}} \cdot \sqrt{(a-b)^{2}+(b-c)^{2}+(c-a)^{2}}}\)
cos θ = 0
⇒ θ =90°

प्रश्न 4.
x- अक्ष के समांतर तथा मूल बिन्दु से जाने वाली रेखा का समी० ज्ञात कीजिए।
हल:
x- अक्ष के दिक् कोसाइन 1, 0, 0 हैं।
∴ x अक्ष के समांतर रेखा के दिक् कोसाइन भी 1, 0, 0 होंगे
अतः रेखा का समी० जो मूल बिन्दु से जाती है जिसमें दिक कोसाइन 1, 0, 0 हैं।

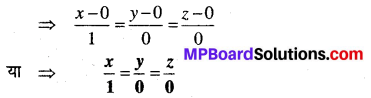
प्रश्न 5.
यदि बिन्दुओं A, B, C और D के निर्देशांक क्रमशः (1, 2, 3), (4, 5, 7) (- 4, 3, – 6) और (2, 9, 2) हैं तो AB और CD रेखाओं के बीच का कोण ज्ञात कीजिए।
हल:
रेखा AB के दिक् अनुपात 4 – 1, 5 – 2, 7 – 3
या 3, 3, 4
इसी प्रकार CD के दिक् अनुपात 2 + 4, 9 – 3, 2 + 6
या 6, 6, 8 हैं।
यह दिक् अनुपात समानुपाती हैं इस प्रकार \(\frac{3}{6}=\frac{3}{6}=\frac{4}{8}\)
इसलिए रेखाओं AB और CD के बीच का कोण 0° हैं।
अतः रेखाएँ समांतर हैं।

प्रश्न 6.
यदि रेखाएँ \(\frac{x-1}{-3}=\frac{y-2}{2 k}=\frac{z-3}{2}\) और \(\frac{x-1}{3 k}=\frac{y-1}{1}=\frac{z-6}{-5}\) परस्पर लंब हों तो k का मान ज्ञात कीजिए।
हल:
दी गयी रेखाओं के दिक् अनुपात – 3, 2k, 2 और 3k, 1, – 5 हैं।
∵ रेखाएँ परस्पर लंब है तब a₁a₂ + b₁b₂+ c₁c₂ = 0
∴ – 3.3k + 2k.1+ 2.(- 5) = 0
⇒ 9k + 2k – 10 = 0
– 7k = 10
k = \(\frac{-10}{7}\)

प्रश्न 7.
बिन्दु (1, 2, 3) से जाने वाली तथा तल \(\vec{r}=(\vec{i}+2 \vec{j}-5 \vec{k})\) + 9 = 0 पर लंबवत् रेखा का सदिश समी० ज्ञात कीजिए।
हल:
दिया है:
समतल का समी०
\(\vec{r} \cdot(\hat{i}+2 \hat{j}-5 \hat{k})+9\) = 0
∴ समतल के अभिलंब के दिक् अनुपात 1, 2, – 5 होंगे।
∴ बिन्दु (1, 2, 3) से जाने वाले समतल का सदिश समीकरण होगा।
\(\vec{r}=\hat{i}+2 \hat{j}+3 \hat{k}+l(\hat{i}+2 \hat{j}-5 \hat{k})\)

प्रश्न 8.
बिन्दु (a, b, c) से जाने वाले तथा तल \(\vec{r} \cdot(\hat{i}+\hat{j}+\hat{k})\) = 2 के समांतर तल का समीकरण ज्ञात कीजिए।
हल:
दिये गये तल के समांतर तल का समी०

प्रश्न 9.
रेखाओं \(\vec{r}=6 \hat{i}+2 \hat{j}+2 \hat{k}+\lambda(\hat{i}-2 \hat{j}+2 \hat{k})\) और \(\vec{r}=-4 \hat{i}-\hat{k}+\mu(3 \hat{i}-2 \hat{j}-2 \hat{k})\) के बीच की न्यूनतम दूरी ज्ञात कीजिए।
हल:
यदि दो बिन्दु , a2 रेखा पर और b1 और 22 उनकी direction तब उनके बीच न्यूनतम दूरी

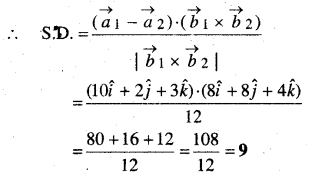
प्रश्न 10.
उस बिन्दु के निर्देशांक ज्ञात कीजिए जहाँ बिन्दुओं (5, 1, 6) और (3, 4, 1) को मिलाने वाली रेखा YZ-तल को काटती है।
हल:
बिन्दु (x₁, y₁, z₁ ) और (x₁, y₁, z₁) को मिलाने वाली रेखा का समीकरण

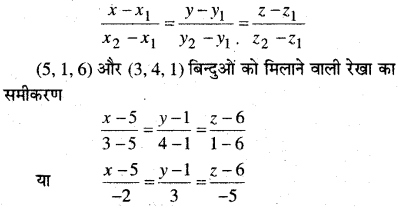
प्रश्न 11.
उस बिन्दु के निर्देशांक ज्ञात कीजिए जहाँ बिन्दुओं (5, 1, 6) और (3, 4, 1) को मिलाने वाली रेखा ZX- तल को काटती है।
हल:
यहाँ बिन्दु (5, 1, 6) और (3, 4, 1) को मिलाने वाली रेखा

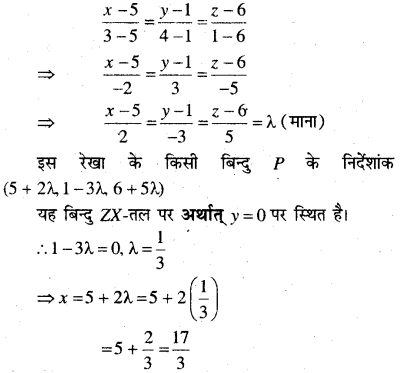
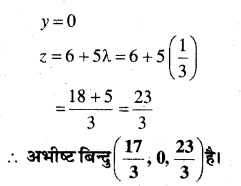
प्रश्न 12.
उस बिन्दु के निर्देशांक ज्ञात कीजिए जहाँ बिन्दुओं (3, – 4, – 5) और (2, – 3, 1) से गुजरने वाली रेखा, समतल 2x + y + z = 7 के पार जाती है।
हल:
दो बिन्दु (3, -4, -5) और (2, -3, 1) से होकर जाने वाली रेखा का समीकरण ।

प्रश्न 13.
बिन्दु (- 1, 3, 2) से जाने वाले तथा समतलों x + 2y + 3z = 5 और 3x + 3y+ c = 0 में से प्रत्येक पर लम्ब समतल का समीकरण ज्ञात कीजिए।
हल:
माना बिन्दु (- 1, 3, 2) से जाने वाले समतल का समीकरण :
a (x + 1) + b(y – 3) + c (z – 2) …(1)
यह समतल x + 2y + 37 = 5 पर लम्ब है।
a + 2b +3c =0 …2
समी० (1) 3x + 3y + x = 0 के अनुलम्ब है।
3a + 3b + c = 0 …(3)
समी० (2) और (3) से,
\(\frac{a}{2-9}=\frac{b}{9-1}=\frac{c}{3-6}\)

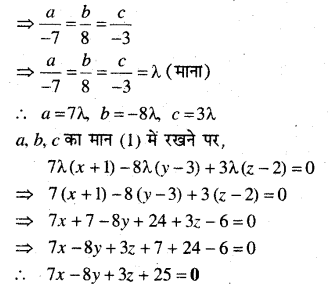
प्रश्न 14.
यदि बिन्दु (1, 1, p) और (-3, 0, 1) समतल 7.(3i +4j -12k) + 13 = 0 से समान दूरी पर स्थित हों तो p का मान ज्ञात कीजिए।
हल:

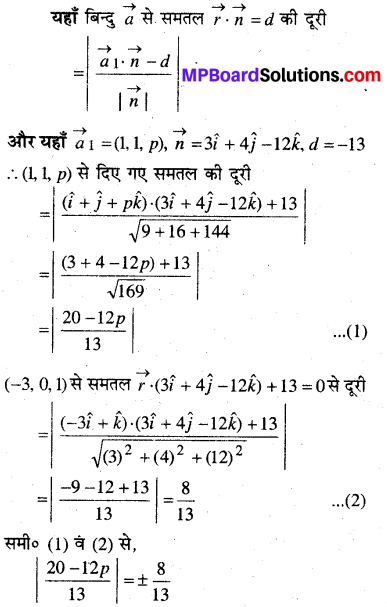
20 – 12p = ± 8
धनात्मक चिन्ह लेने पर,
20 – 12p = 8
12p = 20 – 8 = 12
∴ p=1
ऋणात्मक चिन्ह लेने पर,
20 – 12p = – 8
12p = 20 +8 = 28
p = \(\frac{28}{12}=\frac{7}{3}\)
अतः p=1, \(\frac{7}{3}\)

प्रश्न 15.
समतलों \(\vec{r}(\hat{i}+\hat{j}+\hat{k})\) = 1 और \(\vec{r}(2 \hat{i}+3 \hat{j}\)\(-\hat{k})\) + 4 = 0 के प्रतिच्छेदन रेखा से जाने वाले तथा x-अक्ष के समान्तर तल का समीकरण ज्ञात कीजिए।
हल:
दो समतल [Latex]\overrightarrow{\mathbf{r}}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})[/latex] – 1 = 0 और \(\vec{r} \cdot(2 \hat{i}+3 \hat{j}-\hat{k})\) + 4 = 0 के प्रतिच्छेदन रेखा से जाने वाले 3
समतल का समीकरण

अतः यह अभीष्ट समतल का समीकरण है।

प्रश्न 16.
यदि मूल बिन्दु 0 तथा बिन्दु P के निर्देशांक (1, 2, – 3) हैं तो बिन्दु P से जाने वाले तथा OP के लम्बवत्तल का समीकरण ज्ञात कीजिए।
हल:
यहाँ बिन्दु O(0, 0, 0) और P(1, 2, –3) से होकर जाने वाली रेखा का दिक्-अनुपात OP, 1-0, 2-0, -3 -0 या
1, 2, -3 हैं।
⇒ अभीष्ट समतल के लम्ब के दिक्-अनुपात (1, 2, – 3)
और समतल P(1, 2, – 3) से होकर जाता है।
a (x – x₁) + b (y – y₁) + c (z – z₁) = 0
1.(x – 1) + 2 (y – 2) – 3(z + 3) = 0
⇒ x – 1 + 2y – 4 – 3z -9 = 0
∴ x + 2y – 37 – 14 = 0
यही अभीष्ट समतल का समीकरण है।

प्रश्न 17.
समतलों \(\vec{r} \cdot(\hat{i}+2 \hat{j}+3 \hat{k})\) – 4 = 0 और \(\vec{r} \cdot(2 \hat{i}+\hat{j}-\hat{k})\) + 5 = 0 के प्रतिच्छेदन रेखा को अंतर्विष्ट करने वाले तथा तल 7 (5i +3j-6k) +8 = 0 के लम्बवत् तल का समीकरण ज्ञात कीजिए।
हल:
दिए गए समतल

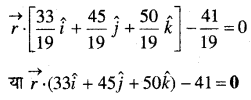
प्रश्न 18.
बिन्दु (- 1,- 5, – 10) से रेखा \(\vec{r}=2 \hat{i}-\hat{j}+2 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+2 \hat{k})\) और समतल \(\vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})\) = 5 के प्रतिच्छेदन बिन्दु के मध्य की दूरी ज्ञात कीजिए।
हल:
यहाँ रेखा

प्रश्न 19.
बिन्दु (1, 2, 3) से जाने वाली तथा समतलों \(\vec{r} \cdot(\hat{i}-\hat{j}+2 \hat{k})\) = 5 और \(\vec{r} \cdot(3 \hat{i}+\hat{j}+\hat{k})\) = 6 के समान्तर रेखा का सदिश समीकरण ज्ञात कीजिए।
हल:
माना बिन्दु (1, 2, 3) से होकर जाने वाली रेखा का समीकरण

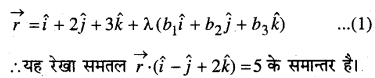
समतल का अभिलम्ब और रेखा (1) परस्पर लम्बवत् हैं।
∴ b₁ – b₂ + 2b₃ = 0

प्रश्न 20.
बिन्दु (1, 2, – 4) से जाने वाली और दोनों रेखाओं \(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\) और \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\) पर लम्ब रेखा का सदिश समीकरण ज्ञात कीजिए।
हल:
माना अभीष्ट रेखा

प्रश्न 21.
यदि एक समतल के अन्तःखण्ड a,b,c हैं और इसकी मूल बिन्दु से दूरी p इकाई है तो सिद्ध कीजिए कि
\(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{p^{2}}\)
हल:

प्रश्न 22 और 23 में सही उत्तर का चयन कीजिए।
प्रश्न 22.
दो समतलों 2x + 3y + 4z =4 और 4x + 6y + 8z = 12 के बीच की दूरी है-
(A) 2 इकाई
(B) 4 इकाई
(C) 8 इकाई
(D)\(\frac{2}{\sqrt{29}}\) इकाई।
हल:
समतलों का समीकरण
2x + 3y + 4z = 4 …(1)
4x + 6y + 8z = 12 …(2)
समी० (2) में 2 से भाग करने पर,
2x + 3y + 4z = 6 …(3)
समतलों के बीच की दूरी
ax + by + cz = d₁, और ax + by + cz = d₂

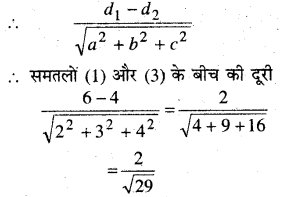
अतः विकल्प (D) सही है।

प्रश्न 23.
समतल 2x – y + 4z = 5 और 5x – 2.5y + 10z = 6 हैं-
(A) परस्पर लम्ब
(B) समान्तर
(C) y-अक्ष पर प्रतिच्छेदन करते हैं
(D) बिन्दु \(\left(0,0, \frac{5}{4}\right)\) से गुजरते हैं।
हल:
समतलों के समीकरण
2x – y + 4z = 5 …(1)
5x – 2.5y + 10z = 6 …(2)
x, y, z के गुणांकों की तुलना करने पर

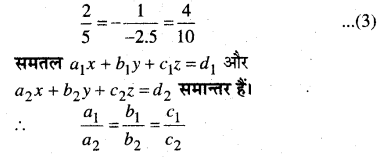
(1) व (2) समान्तर हैं।
अतः विकल्प (B) सही है।