MP Board Class 11th Maths Solutions Chapter 6 सम्मिश्र संख्याएँ और द्विघातीय समीकरण विविध प्रश्नावली
प्रश्न 1 से 6 तक की असमिकाओं को हल कीजिए :
प्रश्न 1.
2 ≤ 3x – 4 ≤ 5.
हल:
∵ 2 ≤ 3x – 4 ≤ 5
या 2 + 4 ≤ 3x ≤ 5 + 4
या 6 ≤ 3x ≤ 9
3 से दोनों पक्षों में भाग देने पर 2 ≤ x ≤ 3
∴ दी हुई असमिका का हल = [2, 3].
प्रश्न 2.
6 ≤ – 3 (2x – 4) < 12.
हल:
6 ≤ – 3(2x – 4) < 12 6 ≤ – 6(x – 2) > 12
– 6 से भाग करने पर
– 1 ≥ x – 2 > – 2;
– 1 + 2 ≥ x > – 2 + 2
1 ≥ x > 0 या 0 < x ≤ 1
दी हुई असमिका का इल (0, 1].
प्रश्न 3.
– 3 ≤ 4 – \(\frac{7 x}{2}\) ≤ 18
हल:
दी हुई असमिका – 3 ≤ 4 – \(\frac{7 x}{2}\) ≤ 18
2 से गुणा करने पर
– 6 ≤ 8 – 7x ≤ 36
8 घटाने पर,
– 14 ≤ – 7x ≤ 28
– 7 से भाग देने पर 2 ≥ x ≥ – 4 या – 4 ≤ x ≤ 2
∴ दी हुई असमिका का हल [- 4, 2].
![]()
प्रश्न 4.
– 15 < 3 \(\frac{3(x-2)}{5}\) ≤ 0
हल:
– 15 < 3 \(\frac{3(x-2)}{5}\) ≤ 0
5 से गुणा करने पर
– 75 < 3x – 6 ≤ 0
– 75 + 6 < 3x ≤ 6
3 से भाग देने पर
\(\frac{-69}{3}\) < x ≤ 2 या – 23 < x ≤ 2
∴ असमिका का हल = (- 23 , 2].
प्रश्न 5.
– 12 < 4 – \(\frac{3 x}{-5}\) ≤ 2
हल:

प्रश्न 6.
7 ≤ \(\frac{3 x+11}{2}\) ≤ 11.
हल:
7 ≤ \(\frac{3 x+11}{2}\) ≤ 11 2 से गुणा करने पर 14 ≤ 3x + 11 ≤ 22 11 घटाने पर 3 ≤ 3x ≤ 11 3 से भाग देने पर 1 ≤ x ≤ \(\frac{11}{3}\)
∴ असमिका का हल = [1, \(\frac{11}{3}\)].
प्रश्न 7 से 12 तक की असमिकाओं को हल कीजिए और उनके हल को संख्या-रेखा पर निरूपित कीजिए :
प्रश्न 7.
5x + 1 > – 24, 5x – 1 < 24. हल: (i) 5x + 1 > – 24 या 5x > – 25 या x > – 5
(ii) 5x – 1 < 24 या 5x < 25
∴ x < 5
∴ असमिकाओं का हल (-5, 5).
इसका संख्या रेखा द्वारा निरूपण इस प्रकार है :
![]()
प्रश्न 8.
2(x – 1) < x + 5, 3(x + 2) > 2 – x.
हल:
दी हुई असमिकाएँ
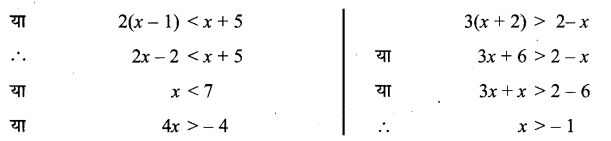
असमिकाओं का हल (- 1, 7).
![]()
![]()
प्रश्न 9.
3x – 7 > 2(x -6), 6 – x > 11 – 2x.
हल:
दी हुइ असमिकाएँ
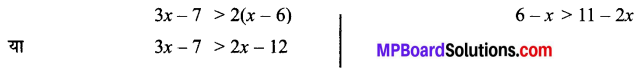

दी हुई असमिकाओं का हल (5, ∞ ) है और संख्या रेखा पर निरूपण इस प्रकार है।
![]()
प्रश्न 10.
5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47.
हल:
दी हुई असमिकाएँ
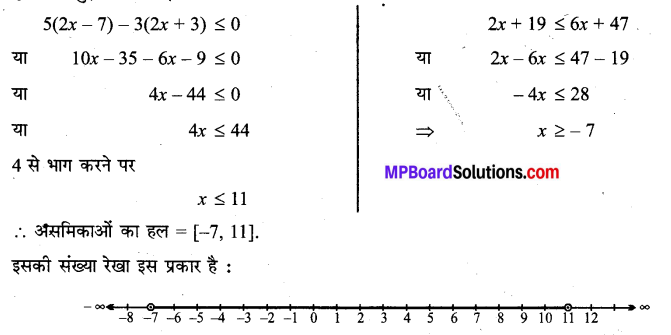
प्रश्न 11.
एक विलयन को 68°F और 77°F के मध्य रखना है। सेल्सियस पैमाने पर विलयन के तापमान का परिसर ज्ञात कीजिए, जहाँ सेल्सियस फारेनहाइट परिवर्तन सूत्र F = \(\frac{9}{5}\) C + 32 है।
हल :

\(\frac{5}{9}\) से गुणा करने पर
20° < C < 25°
∴ C का परिसर अंतराल (20°, 25°).
![]()
प्रश्न 12.
8% बोरिक एसिड के विलयन में 2% बोरिक एसिड का विलयन मिलाकर तनु (dilute) किया जाता है। परिणामी मिश्रण में बोरिक एसिड 4% से अधिक तथा 6% से कम होना चाहिए। यदि हमारे पास 8% विलयन की मात्रा 640 लीटर हो तो ज्ञात कीजिए कि 2% विलयन के कितने लीटर इसमें मिलाने होंगे?
हल:
माना 2% बोरिक एसिड का x लीटर विलयन मिलाया जाता है।
कुल मिश्रण की संख्या = 640 + x
(i) यदि मिश्रण में 4% से अधिक का विलयन है तो

इस प्रकार 2% एसिड विलयन की मात्रा 320 मीटर से-अभिक और 1280 लीटर से कम होनी चाहिए।
प्रश्न 13.
45% अम्ल के 1125 लीटर विलयन में कितना पानी मिलाया लाए कि परिणामी मिश्रण में अम्ल 25% से अधिक परन्तु 30% से कम हो जाए?
हल:
मान लीजिए 45% एसिड विलयन में x लीटर पानी मिलाया जाए, तो मिश्रण की कुल मात्रा
= 1125 + x लीटर


अर्थात् 562.5 लीटर से अधिक किंतु 900 लीटर से कम।
![]()
प्रश्न 14.
एक व्यक्ति के बोद्धिक-लब्धि (I.Q.) मापन का सूत्र निम्नलिखित है :
IQ= [Latex]\frac{M A}{C A}[/Latex] × 100
जहाँ MA मानसिक आयु और CA कालावकि भा है। दि 12 वर्ष की आयु के बच्चों के एक समूह की IQ, असमिका 80 ≤ IQ ≤ 140 द्वारा प्रबत हो तो इस समूह के बच्चों की मानसिक आयु का परिसर ज्ञात कीजिए।

अत: मानसिक आयु कम से कम 9.6 वर्ष है और अधिक से अधिक 16.8 वर्ष है।