In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 4 Quadratic Equations Ex 4.3 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 4 Quadratic Equations Ex 4.3
![]()
Question 1.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x + 3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4\(\sqrt{3}\)x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solution:
(i) We have, 2x2 – 7x + 3 = 0
Dividing both sides by 2, we get

(ii) We have 2x2 + x – 4 = 0
Divide both sides by 2, we get
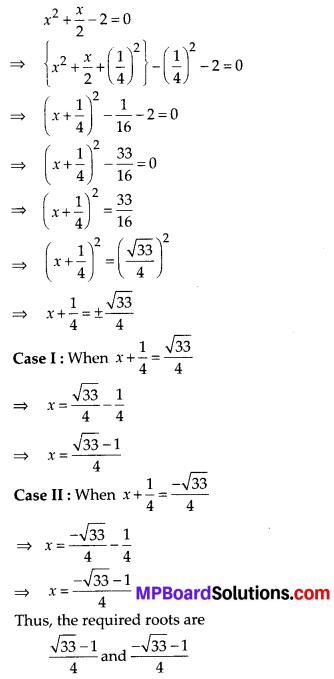
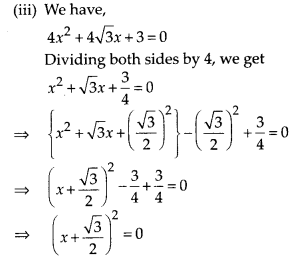

(iv) We have, 2x2 + x + 4 = 0
Dividing both sides by 2, we get

Since, the square of a number cannot be negative.
∴ There is no real value of x satisfying the given equation.
![]()
Question 2.
Find the roots of the following quadratic equations, using the quadratic formula:
(i) 2x2 – 7x + 3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4\(\sqrt{3}\)x + 3 = 0
(iv) 2x2 + x + 4 = 0
Solution:
(i) Comparing the given equation with ax2 + bx + c = 0, we get a = 2, b = -7, c = 3
∴ b2 – 4ac = (-7)2 – 4(2)(3) = 49 – 24 = 25 > 0
Since b2 – 4ac > 0, therefore the given equation has real roots, which are given by

Taking negative sign, x = \(\frac{7-5}{4}=\frac{2}{4}=\frac{1}{2}\)
Thus, the roots of the given equation are 3 and \(\frac{1}{2}\).
(ii) Comparing the given equation with ax2 + bx + c = 0, we get a = 2, b = 1, c = – 4
b2 – 4ac = (1)2 – 4(2)(-4) = 1 + 32 = 33 > 0
Since b2 – 4ac > 0, therefore the given equation has real roots, which are given by

(iii) Comparing the given equation with
ax2 + bx + c = 0, we get
a = 4, b= 473, c = 3
b2 – 4ac = (473)2 – 4(4)(3)
= (16 × 3) – 48 = 48 – 48 = 0
Since b2 – 4ac = 0, therefore the given equation has real and equal roots, which are given by

(iv) Comparing the given equation with ax2 + bx + c = 0, we get a = 2, b = 1, c = 4
b2 – 4ac = (1 )2 – 4(2)(4) = 1 – 32 = -31 < 0 Since
b2 – 4ac < 0, therefore the given equation does not have real roots.
![]()
Question 3.
Find the roots of the following equations:
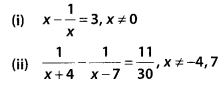
Solution:


Taking negative sign, x = \(\frac{3-1}{2}\)
Thus, the required roots of the given equation are 2 and 1.
Question 4.
The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is \(\frac{1}{3}\). Find his present age.
Solution:
Let the present age of Rehman be x years.
3 years ago, Rehman’s age = (x – 3) years
5 years later, Rehman’s age = (x + 5) years
According to the condition,

⇒ 3(2x + 2) = x2 + 2x – 15
⇒ 6x + 6 = x2 + 2x – 15
⇒ x2 + 2x – 6x – 15 – 6 = 0
⇒ x2 – 4x – 21 = 0 …(1)
Comparing equation (1) with ax2 + bx + c = 0,
we get a = 1, b = -4, c = -21
b2 – 4ac = (-4)2 – 4(1)(-21) = 16 + 84 = 100
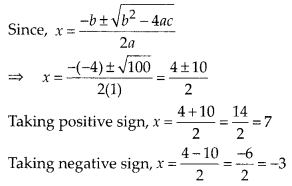
Since, age cannot be negative.
∴ x ≠ -3 ⇒ x = 7
So, the present age of Rehman = 7 years
Question 5.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Solution:
Let Shefali’s marks in Mathematics = x
∴ Marks in English = 30 – x
According to the condition,
(x + 2) × [(30 – x) – 3] = 210
⇒ (x + 2) × (30 – x – 3) = 210
⇒ (x + 2)(- x + 27) = 210
⇒ -x2 + 25x + 54 = 210
⇒ -x2 + 25x + 54 – 210 = 0
⇒ -x2 + 25x – 156 = 0
⇒ x2 – 25x + 156 = 0 …(1)
Comparing equation (1) with ax2 + bx + c = 0, we get a = 1,b = -25, c = 156
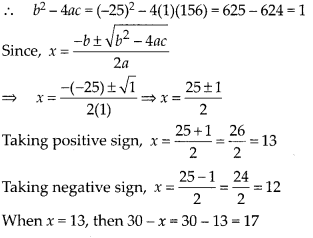
When x = 12, then 30 – x = 30 – 12 = 18 Thus, marks in Mathematics = 13, marks in English = 17 or
Marks in Mathematics = 12, Marks in English = 18.
![]()
Question 6.
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Solution:
Let the shorter side i.e., breadth = x metres
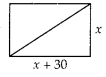
∴ The longer side i.e., length = (x + 30) metres and diagonal = (x + 60) metres
In a rectangle,
(diagonal)2 = (breadth)2 + (length)2
⇒ (x + 60)2 = x2 + (x + 30)2
⇒ x2 + 120 x + 3600 = x2 + x2 + 60x + 900
⇒ x2 + 120x + 3600 = 2x2 + 60x + 900
⇒ 2x2 – x2 + 60x – 120x + 900 – 3600 = 0
⇒ x2 – 60x – 2700 = 0 …(1)
Comparing equation (1) with ax2 + bx + c = 0, we get a = 1, b = -60, c = -2700
∴ b2 – 4ac = (-60)2 – 4(1)(-2700)
⇒ b2 – 4ac = 3600 + 10800
⇒ b2 – 4ac = 14400
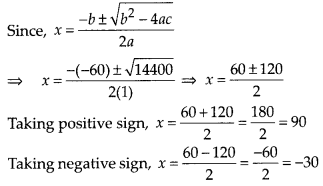
Since breadth cannot be negative,
x ≠ -30 ⇒ x = 90
∴ x + 30 = 90 + 30 = 120
Thus, the shorter side is 90 m and the longer side is 120 m.
Question 7.
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Solution:
Let the larger number be x.
Since, (smaller number)2 = 8(larger number)
⇒ (smaller number)2 = 8
⇒ smaller number = \(\sqrt{8 x}\)
According to the condition,

Thus, the smaller number = 12 or -12
Thus, the two numbers are 18 and 12 or 18 and -12.
Question 8.
A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:


Thus, speed of the train is 40 km/hr.
Question 9.
Two water taps together can fill a tank in \(9 \frac{3}{8}\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Let the smaller tap fills the tank in x hours
∴ The larger tap fills the tank in (x – 10) hours.
Amount of water flowing through both the taps in one hour


[ ∵ Time cannot be negative]
x = 25 ⇒ x – 10 = 25 – 10 = 15
Thus, time taken to fill the tank by the smaller tap alone is 25 hours and by the larger tap alone is 15 hours.
Question 10.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let the average speed of the passenger train be x km/h.
∴ Average speed of the express train = (x + 11) km/h
Total distance covered = 132 km

Comparing equation (1) with ax2 + bx + c = 0, we get a = 1, b = 11, c = -1452

Question 11.
Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let the side of the smaller square be x m.
⇒ Perimeter of the smaller square = 4x m
∴ Perimeter of the larger square = (4x + 24) m
⇒ Side of the larger square
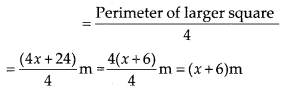
Area of the smaller square = x2 m2
Area of the larger square = (x + 6)2 m2
According to the condition,
x2 + (x + 6)2 = 468
⇒ x2 + x2 + 12x + 36 = 468
⇒ 2x2 + 12x – 432 = 0
⇒ x2 + 6x – 216 = 0 …(1)
[Dividing both sides by 2] Comparing equation (1) with ax2 + bx + c = 0, we get
a = 1, b = 6, c = -216
b2 – 4ac = (6)2 – 4(1)(-216) = 36 + 864 = 900

But the length of a square cannot be negative,
∴ x ≠ -18 ⇒ x = 12
Length of the smaller square = 12 m
and the length of the larger square = x + 6
= 12+ 6 = 18 m