In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 2 Polynomials Ex 2.2 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 2 Polynomials Ex 2.2
Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solution:
(i) we have p(x) = x2 – 2x – 8
= x2 + 2x + – 4x – 8
= x(x + 2) – 4(x + 2)
= (x – 4)(x + 2)
For p(x) = 0, we must have (x – 4)(x + 2) = 0
Either x – 4 = 0 ⇒ x = 4
or x + 2 = 0 ⇒ x = -2
∴ The zeroes of x2 – 2x – 8 are 4 and -2
Now, sum of zeroes

![]()
Thus, the relationship between the zeroes and the coefficients in the polynomial x2 – 2x – 8 is verified.
![]()
(ii) We have p(s) = 4s2 – 4s + 1
= 4s2 – 2s – 2s + 1
= 2s(2s – 1) – l(2s – 1)
= (2s – 1)(2s – 1)

Thus, the relationship between the zeroes and coefficients in the polynomial 4s2 – 4s + 1 is verified.
(iii) We have p(x) = 6x2 – 3 – 7x
= 6x2 – 7x – 3
= 6x2 – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (3x + 1)(2x – 3)
For p(x) = 0, we have,

Thus, the relationship between the zeroes and coefficients in the polynomial 6x2 – 3 – 7x is verified.
![]()
(iv) We have, p(u) = 4u2 + 8u = 4u(u + 2)
For p(u) = 0,
we have
Either 4u = 0 ⇒ u = 0
or u + 2 = 0 ⇒ u = -2
∴ The zeroes of 4u2 + 8u are 0 and – 2.
Now, 4u2 + 8u can be written as 4u2 + 8u + 0.

Thus, the relationship between the zeroes and coefficients in the polynomial 4u2 – 4s + 1 is verified.
![]()
(v) We have, p(t) = t2 – 15 = (t)2 – \((\sqrt{15})^{2}\)

Thus, the relationship between zeroes and the coefficients in the polynomial t2 – 15 is verified.
(vi) We have, p(x) = 3x2 – x – 4
= 3x2 + 3x – 4x – 4
= 3x(x + 1) – 4(x + 1)
= (x + 1)(3x – 4)
For p(x) = 0 we have,
Either (x + 1) = 0 ⇒ x = -1

Thus, the relationship between the zeroes and coefficients in the polynomial 3x2 – x – 4 is verified
![]()
Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) \(\frac{1}{4}\), -1
(ii) \(\sqrt{2}, \frac{1}{3}\)
(iii) 0, \(\sqrt{5}\)
(iv) 1, 1
(v) \(-\frac{1}{4}, \frac{1}{4}\)
(vi) 4,1
Solution:
(i) Since, sum of zeroes, \((\alpha+\beta)=\frac{1}{4}\)
Product of zeroes, αβ = -1
∴ The required quadratic polynomial is

have samezeroes, therefore (4x2 – x – 4) is the required quadratic polynomial.
(ii) Since, sum of zeroes, \((\alpha+\beta)=\sqrt{2}\)
product of zeroes, αβ = \(\frac{1}{3}\)
∴ The required quadratic polynomial is

(iii) Since, sum of zeroes, (α + β) = 0
Product of zeroes, αβ = \(\sqrt{5}\)
∴ The required quadratic polynomial is
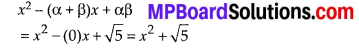
(iv) Since, sum of zeroes, (α + β) = 1
Product of zeroes, αβ = 1
∴ The required quadratic polynomial is
![]()
(v) Since, sum of zeroes, (α + β) = \(-\frac{1}{4}\)
Product of zeroes, αβ = \(\)[\frac{1}{4}/latex]
∴ The required quadratic polynomial is

same zeroes, therefore, the required quadratic polynomial is (4x2 + x + 1)
(vi) Since, sum of zeroes, (α + β) = 4 and
product of zeroes, αβ = 1
∴ The required quadratic polynomial is
x2 – (α + β)x + αβ = x2 – 4x + 1