MP Board Class 10th Maths Solutions Chapter 14 Statistics Ex 14.1

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 14 Statistics Ex 14.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 14 Statistics Ex 14.1

Question 1.
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

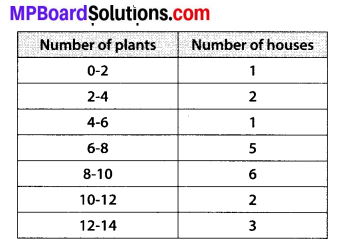
Which method did you use for finding the mean, and why?
Solution:
We can calculate the mean as follows :

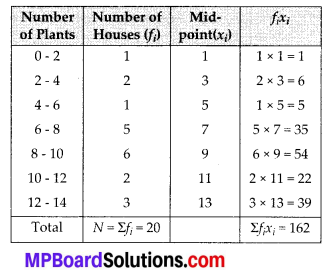
∴ Mean = \(\overline{x}=\frac{\sum f_{i} x_{i}}{N}=\frac{162}{20}=8.1\)
Thus, mean number of plants per house is 8.1 Since, values of x_i and f_i are small, so we have used the direct method.

Question 2.
Consider the following distribution of daily wages of 50 workers of a factory.

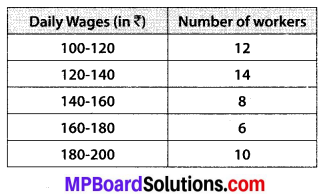
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
Let the assumed mean, a = 150
∵ Class size, h = 20
∴ \(u_{i}=\frac{x_{i}-a}{h}=\frac{x_{i}-150}{20}\)
∴ We have the following table:

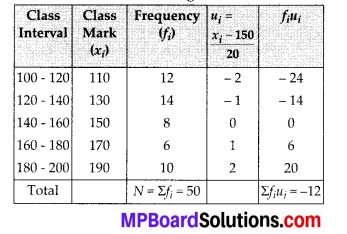
Now, \(\overline{x}\) = a + h × {\(\frac{1}{N}\) Σf_iu_i}
= 150 + 20 × \(\left(\frac{-12}{50}\right)\) = 150 – \(\frac{24}{5}\)
= 150 – 4.8 = 145.20

Question 3.
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f.

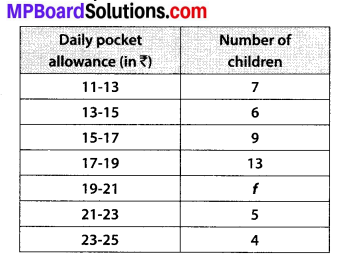
Solution:
Let the assumed mean, a = 18
∵ Class size, h = 2
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-18}{2}\)
Now, we have the following table:

⇒ [f + 44] (0) = 2[f – 20]
⇒ 2[f – 20] = 0 ⇒ f = 20
Thus, missing frequency is 20.

Question 4.
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.

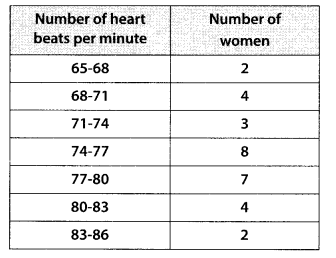
Solution:
Let the assumed mean, a = 75.5
∵ Class size, h = 3
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-75.5}{3}\)
Now, we have the following table:

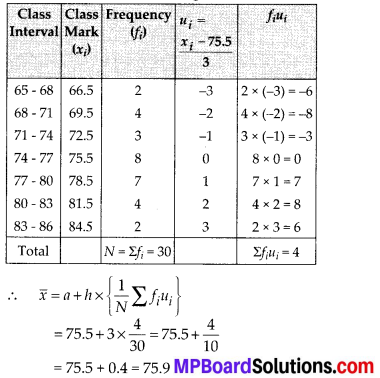
Thus, the mean heart beats per minute is 75.9.

Question 5.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained a varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

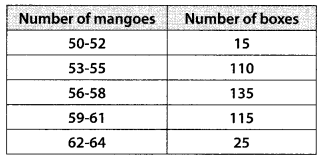
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:
Let the assumed mean, a = 57
∴ d_i = x_i – 57
Now, we have the following table:

Thus, the average number of mangoes per box = 57.19. We choose assumed mean method.

Question 6.
The table below shows the daily expenditure on food of 25 households in a locality.

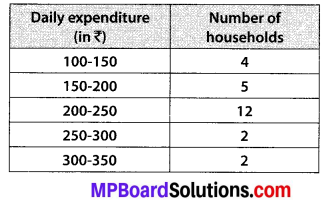
Find the mean daily expenditure on food by a suitable method.
Solution:
Let the assumed mean, a = 225
∵ Class size, (h) = 50
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-225}{50}\)
Now, we have the following table:

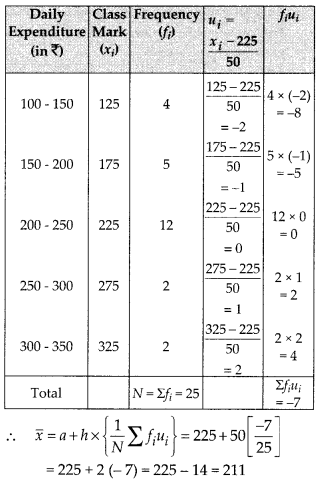
Thus, the mean daily expenditure on food is ₹ 211.

Question 7.
To find out the concentration of S0₂ in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:

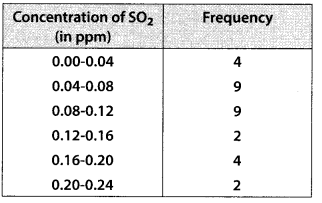
Find the mean concentration of S0₂ in the air.
Solution:
Let the assumed mean, a = 0.14
∵ Class size, (h) = 0.04
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-0.14}{0.04}\)
Now, we have the following table:

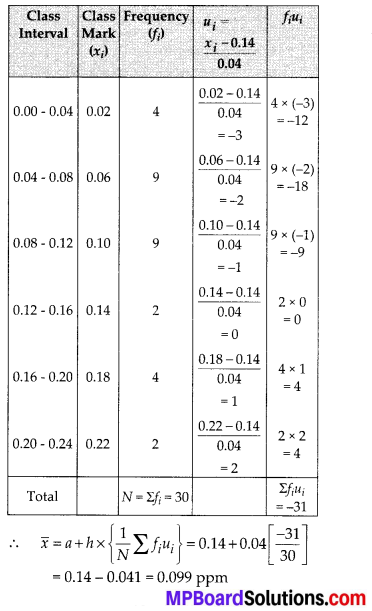
Question 8.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

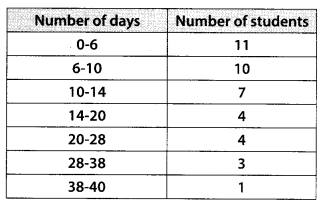
Solution:
Using the direct method, we have the following table:

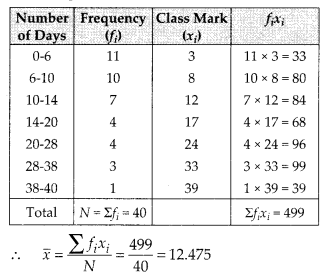
Thus, mean number of days a student remained absent = 12.48.

Question 9.
The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.

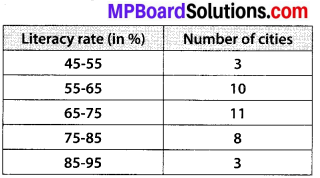
Solution:
Let the assumed mean, a = 70
∵ Class size, (h) = 10
∴ u_i = \(\frac{x_{i}-a}{h}=\frac{x_{i}-70}{10}\)
Now, we have the following table:

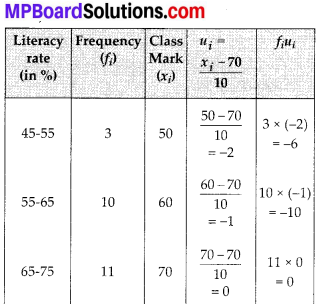
Thus, the mean literacy rate is 69.43%