In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 10th Maths Solutions Chapter 1 वास्तविक संख्याएँ Ex 1.4
प्रश्न 1.
बिना लम्बी विभाजन क्रिया किर बताइए कि निम्नलिखित परिमेय संख्याओं के दशमलव प्रसार सांत है या असांत आवर्ती हैं :
(i) \(\frac { 13 }{ 3125 } \)
(ii) \(\frac { 17 }{ 8 } \)
(iii) \(\frac { 64 }{ 455 } \)
(iv) \(\frac { 15 }{ 1600 } \)
(v) \(\frac { 29 }{ 343 } \)
(vi) \(\frac{23}{2^{3} 5^{2}}\)
(vii) \(\frac{129}{2^{2} 5^{7} 7^{5}}\)
(viii) \(\frac { 6 }{ 15 } \)
(ix) \(\frac { 35 }{ 50 } \)
(x) \(\frac { 77 }{ 210 } \)
हल:
(i) \(\frac { 13 }{ 3125 } \) = \(\frac{13}{5^{5}}\)
चूँकि हर में केवल 5 की धात है।
अतः, दशमलव प्रसार सांत है।
(ii) \(\frac { 17 }{ 8 } \) = \(\frac{17}{2^{3}}\)
चूँकि हर में केवल 2 की घात है।
अतः, दशमलव प्रसार सांत है।
(iii) \(\frac { 64 }{ 455 } \) = \(\frac{64}{5^{1} \times 7^{1} \times 13^{1}}\)
चूँकि हर में 5 के अतिरिक्त 7 एवं 13 की धात हैं।
अतः, दशमलव प्रसार असांत आवर्ती है।
(iv) \(\frac { 15 }{ 1600 } \) = \(\frac{15}{2^{6} \times 5^{2}}\) = \(\frac{3}{2^{6} \times 5^{1}}\)
चूँकि हर में केवल 2 एवं 5 की घातें हैं।
अतः, दशमलव प्रसार सांत है।
(v) \(\frac { 29 }{ 343 } \) = \(\frac{29}{7^{3}}\)
चूँकि हर में 7 की घात है।
अतः, दशमलव प्रसार असांत आवर्ती है।
(vi) \(\frac{23}{2^{3} \times 5^{2}}\) के हर में चूँकि केवल 2 एवं 5 की घातें हैं।
अतः, दशमलव प्रसार सांत होगा।
(vii) \(\frac{129}{2^{2} \times 5^{7} \times 7^{5}}\)
के हर में चूँकि 2 एवं 5 के अतिरिक्त 7 की घातें भी हैं।
अतः, दशमलव प्रसार असांत आवर्ती है।
(viii) चूँकि \(\frac { 6 }{ 15 } \) = \(\frac { 2 }{ 5 } \) के हर में केवल 5 की घात है
अतः, दशमलव प्रसार सांत होगा।
(ix) चूँकि \(\frac { 35 }{ 50 } \) = \(\frac { 7 }{ 10 } \) = \(\frac{7}{2 \times 5}\) के हर में केवल 2 एवं 5 की घातें हैं।
अतः, दशमलव प्रसार सांत होगा।
(x) \(\frac { 77 }{ 210 } \) = \(\frac { 11 }{ 30 } \) = \(\frac{11}{2 \times 3 \times 5}\)
चूँकि इसके हर में 2 और 5 के अतिरिक्त 3 की भी घातें हैं।
अतः, दशमलव प्रसार असांत आवर्ती होगा।
![]()
प्रश्न 2.
ऊपर दिए गए प्रश्न में उन परिमेय संख्याओं के दशमलव प्रसारों को लिखिए जो सांत हैं।
हल:
ऊपर दिए गए प्रश्न में निम्न परिमेय संख्याओं के प्रसार सांत हैं :
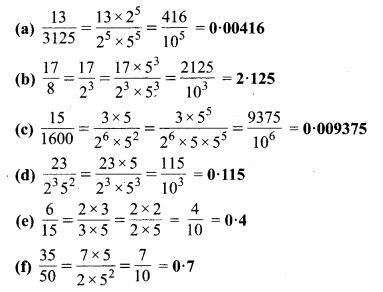
प्रश्न 3.
कुछ वास्तविक संख्याओं के दशमलव प्रसार नीचे दर्शाए गए हैं। प्रत्येक स्थिति के लिए निर्धारित कीजिए कि यह संख्या परिमेय संख्या है या नहीं। यदि यह परिमेय संख्या है और के रूप की है तो के अभाज्य गुणनखण्डों के बारे में आप क्या कह सकते हैं?
(i) 43.123456789
(ii) 0.120120012000120000…..
(iii) \(43 \cdot \overline{123456789}\)
हल:
(i) 43.123456789 = \(\frac{43123456789}{10^{9}}\) 43123456789 में दशमलव प्रसार सांत है। अत: यह परिमेय संख्या है, जो \(\frac { p }{ q } \) के रूप की है तथा q के अभाज्य गुणनखण्ड 2 और 5 ही हैं।
(ii) 0.120120012000120000 …………. का दशमलव प्रसार असांत अनावर्ती है, इसलिए यह एक अपरिमेय संख्या है।
(iii) \(43 \cdot \overline{123456789}\) में दशमलव प्रसार असांत आवर्ती है। अतः यह एक परिमेय संख्या है जो \(\frac { p }{ q } \) के रूप की है तथा q के अभाज्य गुणनखण्डों में 2 या 5 के अतिरिक्त एक अन्य गुणखण्ड है।