MP Board Class 6th Maths Solutions Chapter 7 Fractions Ex 7.6
Question 1.
Solve:

Solution:

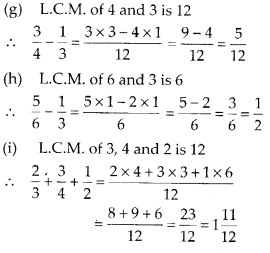

Question 2.
Sarita bought \(\frac{2}{5}\) metre of ribbon and Lalita \(\frac{3}{4}\) metre of ribbon. What is the total length of the
ribbon they bought?
Solution:
Ribbon bought by Sarita = \(\frac{2}{5}\) m
And Ribbon bought by Lalita = \(\frac{3}{4}\) m
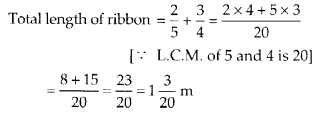
Therefore, they bought 1\(\frac{3}{20}\) m of ribbon.
![]()
Question 3.
Naina was given 1\(\frac{1}{22}\) piece of cake and Najma was given 1\(\frac{1}{3}\) piece of cake. Find the total amount of cake was given to both of them.
Solution:
Cake taken by Naina = 1\(\frac{1}{2}\) piece
And cake taken by Najma = 1\(\frac{1}{3}\) piece
Total cake taken = \(1 \frac{1}{2}+1 \frac{1}{3}=\frac{3}{2}+\frac{4}{3}\)
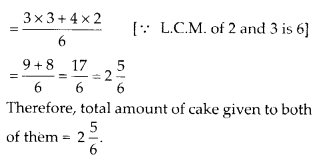
![]()
Question 4.
Fill in the boxes:

Solution:

Question 5.
Complete the addition-subtraction box.
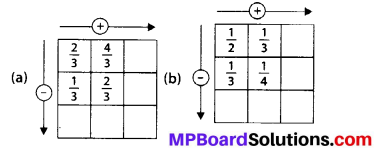
Solution:
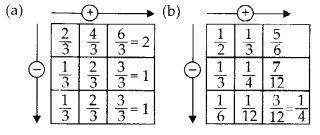
![]()
Question 6.
A piece of wire \(\frac{7}{8}\) metre long broke into two pieces. One piece was \(\frac{1}{4}\) metre long. How long is the other piece?
Solution:
Total length of wire = \(\frac{7}{8}\) metre
Length of first part = \(\frac{1}{4}\) metre
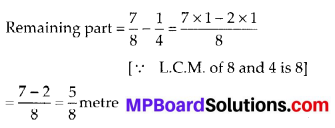
Therefore, the length of remaining part is \(\frac{5}{8}\) metre
Question 7.
Nandini’s house is \(\frac{9}{10}\) metre km from her school. She 10
walked some distance and then took a bus for \(\frac{1}{2}\) metre km to reach the school. How far did she walk?
Solution:
Total distance between school and house = \(\frac{9}{10}\) km
Distance covered bv bus = \(\frac{1}{2}\) km

Therefore, distance covered by walking is \(\frac{2}{5}\) km.
![]()
Question 8.
Asha and Samuel have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{6}\) th full and Samuel’s shelf is \(\frac{2}{5}\)th full. Whose bookshelf is more full? By what fraction?
Solution:

∴ Asha’s bookshelf is more covered than Samuel.
Difference \(=\frac{25}{30}-\frac{12}{30}=\frac{13}{30}\)
![]()
Question 9.
Jaidev takes 2\(\frac{1}{5}\) minutes to walk across the school ground. Rahul takes \(\frac{7}{4}\) minutes to do the same. Who takes less time and by what fraction?
Solution:
