MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.5
पाठ्य-पुस्तक पृष्ठ संख्या # 307-308
प्रश्न 1.
7.3 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { AB } \) = 7.3 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर एक-एक चाप लगाते हैं।
(3) अब B को केन्द्र मानकर और AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर दो चाप और लगाते हैं जो पहले वाले चापों को C और D पर काटते हैं।
(4) C को D से मिलाया। रेखा CD रेखाखण्ड \(\overline { AB } \) को M पर काटती है।
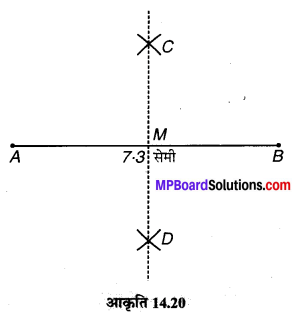
(5) बिन्दु M रेखाखण्ड \(\overline { AB } \) को समद्विभाजित करता है। इस प्रकार प्राप्त रेखाखण्ड सममित अक्ष है।
प्रश्न 2.
9.5 सेमी लम्बा एक रेखाखण्ड खींचिए और उसका लम्ब समद्विभाजक खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड AB = 9.5 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी की. त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं।
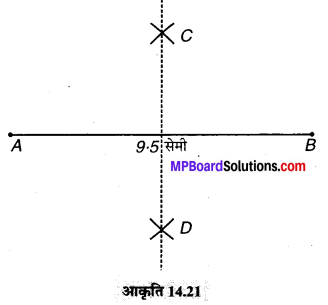
(3) अब B को केन्द्र मानकर इतनी ही त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं, जो पहले चापों को क्रमशः C और D पर काटते हैं।
(4) C को D से मिलाया।
रेखाखण्ड CD अभीष्ट लम्ब समद्विभाजक है।
![]()
प्रश्न 3.
एक रेखाखण्ड \(\overline { XY } \) का लम्ब समद्विभाजक खींचिए जिसकी लम्बाई 10.3 सेमी है।
(a) इस लम्ब समद्विभाजक पर कोई बिन्दु P लीजिए। जाँच कीजिए कि PX = PY है।
(b) यदि M रेखाखण्ड XY का मध्य-बिन्दु है, तो MX और XY के विषय में आप क्या कह सकते हैं ?
हल :
रचना के पद :
(1) रेखाखण्ड \(\overline { XY } \) = 10.3 सेमी खींचते हैं।
(2) X और Y को केन्द्र मानकर और XY के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो एक-दूसरे को A और B पर काटते हैं।
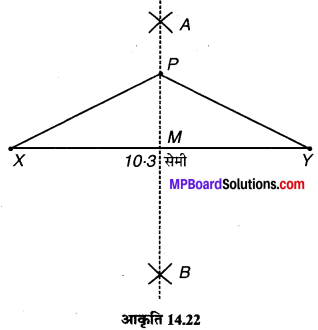
(3) A को B से मिलाया।
इस प्रकार AB ⊥ \(\overline { XY } \)
(4) \(\overline { AB } \) पर कोई बिन्दु P लेते हैं और PX तथा PY को जोड़ते हैं।
(a) मापने पर, \(\overline { PX } \) = \(\overline { PY } \)
(b) \(\overline { XY } \) का मध्य-बिन्दु M है। मापने पर,
\(\overline{X M}=\overline{M Y}=\frac{1}{2} \overline{X Y}\)
प्रश्न 4.
लम्बाई 12.8 सेमी वाला एक रेखाखण्ड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कीजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
(1) रेखाखण्ड AB = 12.8 सेमी खींचा।
(2) AB का लम्ब समद्विभाजक ज्ञात किया जो AB को O पर काटता है।
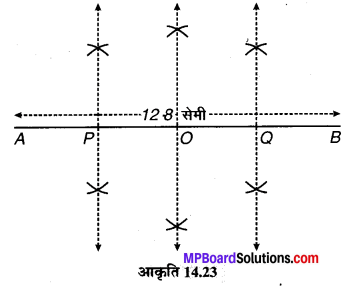
(3) \(\overline { AO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को P पर काटता है।
(4) अब \(\overline { BO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को Q पर काटता है। (Q, \(\overline { OB } \) का मध्य-बिन्दु है।)
(5) रेखाखण्ड \(\overline { AB } \) बिन्दुओं P, O, Q द्वारा चार भागों में विभाजित हो जाता है।
मापने पर, \(\overline{A P}=\overline{P O}=\overline{O Q}=\overline{Q B}=3 \cdot 2\) सेमी
![]()
प्रश्न 5.
6.1 सेमी लम्बाई का एक रेखाखण्ड \(\overline { PQ } \) खींचिए फिर \(\overline { PQ } \) को व्यास मानकर एक वृत्त खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { PQ } \) = 6.1 सेमी खींचा।
(2) \(\overline { PQ } \) का लम्ब समद्विभाजक खींचा जो कि \(\overline { PQ } \) को O पर काटता है। (अर्थात् O, \(\overline { PQ } \) का मध्य-बिन्दु है।)
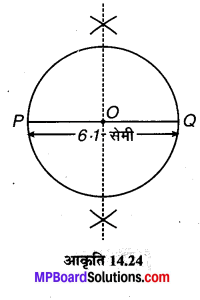
(3) O को केन्द्र मानकर और OP या OQ त्रिज्या लेकर P और Q से जाता हुआ एक वृत्त खींचा।।
वृत्त जिसका कि \(\overline { PQ } \) व्यास है, अभीष्ट वृत्त है।
प्रश्न 6.
केन्द्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा \(\overline { AB } \) खींचिए। इस जीवा \(\overline { AB } \) का लम्ब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केन्द्र C से होकर जाता है ?
हल :
रचना के पद:
(1) कागज पर कोई बिन्दु C लेते हैं।
(2) C को केन्द्र मानकर तथा 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।
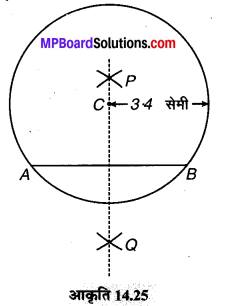
(3) वृत्त की एक जीवा \(\overline { AB } \) खींचते हैं।
(4) वृत्त की जीवा का लम्ब समद्विभाजक PQ खींचते हैं।
हाँ, हम देखते हैं कि यह लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाता है।
![]()
प्रश्न 7.
प्रश्न 6.
की उस स्थिति के लिए दोबारा कीजिए जब \(\overline { AB } \) एक व्यास है।
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O लेते हैं।
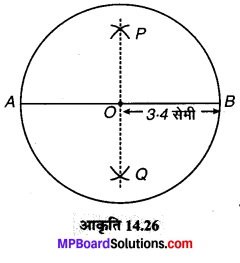
(2) O को केन्द्र मानकर और 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।
(3) वृत्त का व्यास \(\overline { AB } \) खींचते हैं।
(4) \(\overline { AB } \) का लम्ब समद्विभाजक खींचते हैं। हम देखते हैं कि PQ, केन्द्र C से होकर जाता है और O व्यास \(\overline { AB } \) का मध्य-बिन्दु है।
प्रश्न 8.
4 सेमी त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जीवाओं के लम्ब समद्विभाजक खींचिए। ये कहाँ मिलते हैं ?
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O अंकित करते हैं।
(2) O को केन्द्र मानकर और 4 सेमी त्रिज्या लेकर एक वृत्त खीचते हैं।
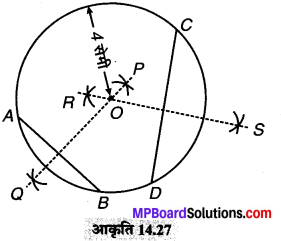
(3) वृत्त की दो जीवाएँ \(\overline { AB } \) और \(\overline { CD } \) खींचते हैं।
(4) जीवा \(\overline { AB } \) का लम्ब समद्विभाजक \(\overline { PQ } \) खींचते है।
(5) जीवा \(\overline { CD } \) का लम्ब समद्विभाजक \(\overline { RS } \) खींचते हैं।
ये दोनों लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाते हैं।
![]()
प्रश्न 9.
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर बिन्दु A और दूसरी भुजा पर एक अन्य बिन्दु B इस प्रकार लीजिए कि OA = OB है। \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक खींचिए। मान लीजिए ये Pपर प्रतिच्छेद करते हैं। क्या PA = PB है ?
हल :
रचना के पद :
(1) कोई कोण XOY बनाते हैं। इसका शीर्ष O है।
(2) \(\overline { OX } \) पर एक बिन्दु A तथा \(\overline { OY } \) पर एक अन्य बिन्दु B लेते हैं।
(3) \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक CD और EF खीचते हैं। माना कि ये P पर मिलते हैं।
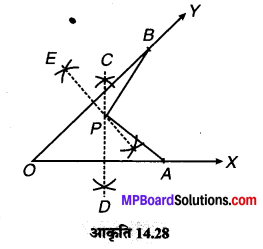
(4) \(\overline { PA } \) और \(\overline { PB } \) को मिलाया
मापने पर, \(\overline{P A}=\overline{P B}\)
पाठ्य-पुस्तक पृष्ठ संख्या # 311
प्रयास कीजिए
प्रश्न 1.
पाठय-पुस्तक में दिए गए चरण 2 में, यदि हम त्रिज्या BC के आधे से कम लें, तो क्या कोण होगा?
उत्तर-
यदि हम BC के आधे से कम त्रिज्या लेंगे तो B तथा C को केन्द्र मानकर खींचे गए चाप आपस में नहीं काटेंगे। अतः कोण नहीं बनेगा।
पाठ्य-पुस्तक पृष्ठ संख्या # 312
प्रश्न 1.
ऊपर दर्शाए अनुसार 60° के कोण की रचना कीजिए। अब इस कोण को समद्विभाजित कीजिए। प्रत्येक कोण 30° का है। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम एक किरण OA खींचते हैं।
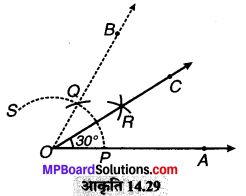
(2) O को केन्द्र मानकर कोई भी उचित त्रिज्या लेकर एक चाप PS लगाते हैं, जो OA को P पर काटता है।
(3) P को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को Q पर काटता है।
(4) OQ को मिलाकर आगे बढ़ाते हैं और किरण OB प्राप्त करते हैं। तब ∠AOB = 60°
(5) P को केन्द्र मानकर और त्रिज्या > \(\frac { 1 }{ 2 }\) PQ लेकर, ∠AOB के अन्तः भाग में एक चाप लगाते हैं।
(6) Q को केन्द्र मानकर इसी त्रिज्या से (चरण 5) एक दूसरा चाप लगाते हैं जो पहले चाप को R पर काटता है।
(7) OR को मिलाते हुए C तक आगे बढ़ाते हैं।
तब ∠AOC = 30°
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 312
प्रयास कीजिए
प्रश्न 1.
15° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम 60° का ∠ABC बनाते हैं।
(2) ∠ABC को संमद्विभाजित करके 30° का कोण प्राप्त करते हैं। अर्थात् ∠ABD = 30°
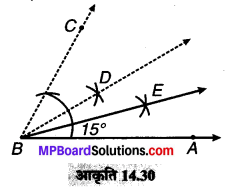
(3) अब ∠ABD को इस प्रकार समद्विभाजित करते हैं कि \(\overline { BE } \) ∠ABD का समद्विभाजिक हो।
इस प्रकार ∠ABE = \(\frac { 1 }{ 2 }\) x 30° = 15°
पाठ्य-पुस्तक पृष्ठ संख्या # 313
प्रयास कीजिए
प्रश्न 1.
150° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम एक रेखा l खींचते हैं और इस पर कोई बिन्दु O लेते हैं।
(2) O को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं, जो l को A पर काटता है।
(3) अब A को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को B पर काटता है।
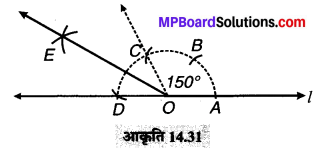
(4) पुनः इसी त्रिज्या से B को केन्द्र मानकर दूसरा चाप लगाते हैं जो पहले चाप को C पर काटता है।
(5) एक बार पुनः इसी त्रिज्या से C को केन्द्र मानकर चाप लगाते हैं जो पहले चाप को D पर काटता है।
(6) अब ∠COD को समद्विभाजित करते हैं,
इस प्रकार ∠COE = ∠EOD = 30°
(7) चूँकि 150° = 120° + 30°
अतः ∠AOC + ∠COE = ∠AOE
अतः अभीष्ट ∠AOE = 150°
![]()
प्रयास कीजिए
प्रश्न 1.
45° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद:
(1) सर्वप्रथम 90° का ∠POQ बनाते हैं।
(2) ∠POQ का समद्विभाजक OR खींचते हैं।
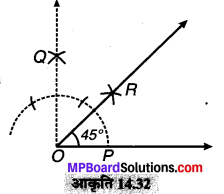
इस प्रकार \(\frac { 1 }{ 2 }\)∠POQ = \(\frac { 1 }{ 2 }\) (90°) = 45°
अतः अभीष्ट ∠POR = 45°