MP Board Class 6th Maths Solutions Chapter 10 Mensuration Ex 10.3

MP Board Class 6th Maths Solutions Chapter 10 Mensuration Ex 10.3

Question 1.
Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Solution:
(a) Area of rectangle = length × breadth
= 3 cm × 4 cm = 12 cm²

(b) Area of rectangle = length × breadth
= 12 m × 21 m = 252 m²

(c) Area of rectangle = length × breadth
= 2 km × 3 km = 6 km²

(d) Area of rectangle = length × breadth
= 2 m × 70 cm = 2 m × 0.7 m = 1.4 m²

Question 2.
Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Solution:
(a) Area of square = side × side
= 10 cm × 10 cm = 100 cm²

(b) Area of square = side × side
= 14 cm × 14 cm = 196 cm²

(c) Area of square = side × side
= 5 m × 5 m = 25 m²

Question 3.
The length and breadth of three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution:
(a) Area of rectangle = length × breadth
= 9m × 6m = 54m²

(b) Area of rectangle = length × breadth
= 17 m × 3 m = 51 m²

(c) Area of rectangle = length × breadth
= 4 m × 14 m = 56 m²
Thus, rectangle (c) has the largest area, i.e. 56 m² and rectangle (b) has the smallest area, i.e., 51 m².

Question 4.
The area of a rectangular garden 50 m long is 300 sq m. Find the width of the garden.
SolutionL
Length of rectangle = 50 m
Area of rectangle = 300 m²
Since, area of rectangle = length × breadth
Therefore, breadth = \(\frac{\text { area of rectangle }}{\text { length }}\)
= \(\frac{300}{50}\) m = 6 m
Thus, the breadth of the garden is 6 m.

Question 5.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of Rs. 8 per hundred sq m?
Solution:
Length of land = 500 m
Breadth of land = 200 m
Area of land = length × breadth
= 500 m × 200 m = 1,00,000 sq m
Cost of tiling 100 sq m of land = Rs. 8
∴ Cost of tiling 1,00,000 sq m of land
= Rs. \(\frac{8 \times 100000}{100}\) = Rs. 8000

Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solution:
Length of table-top = 2 m
Breadth of table-top = 1 m 50 cm = 1.50 m
∴ Area of table-top = length × breadth
= 2 m × 1.50 m = 3 m²

Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution:
Length of room = 4 m
And breadth of room = 3 m 50 cm = 3.50 m
∴ Area of carpet = length × breadth
= 4 m × 3.50 m = 14 m²

Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
Length of floor = 5 m
And breadth of floor = 4 m
Area of floor = length × breadth
= 5m × 4m = 20m²
Now, side of square carpet = 3 m
Area of square carpet = side × side
= 3m × 3m = 9m²
∴ Area of floor that is not carpeted
= 20 m² – 9 m² = 11 m²

Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solution:
Side of square flower bed = 1 m Area of square flower bed = side × side
= 1m × 1m = 1m²
∴ Area of 5 square flower beds = (1 × 5) m²
= 5 m²
Now, length of land = 5 m
And breadth of land = 4 m
∴ Area of land = length × breadth = 5m × 4m
= 20 m²
∴ Area of remaining part
= Area of land – Area of 5 flower beds
= 20 m² – 5 m² = 15 m²

Question 10.
By splitting the following figures into rectangles, find their areas (The measures are given in centimeters).

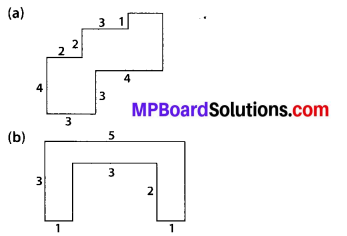
Solution:
(a) We have,

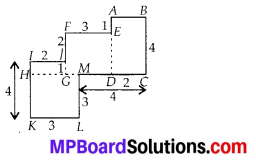
Area of square HKLM = 3 × 3 cm² = 9 cm²
Area of rectangle I]CH = 1 × 2 cm² = 2 cm²
Area of square FEDG = 3 × 3 cm² = 9 cm²
Area of rectangle ABCD = 2 × 4 cm² = 8 cm²
∴ Total area of the figure = (9 + 2 + 9 + 8) cm² = 28 cm²

(b) We have,

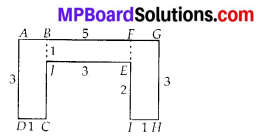
Area of rectangle ABCD = 3 × 1 cm² = 3 cm²
Area of rectangle BJEF = 3 × 1 cm² = 3 cm²
Area of rectangle FGHI = 3 × 1 cm² = 3 cm²
∴ Total area of the figure = (3 + 3 + 3) cm² = 9 cm²

Question 11.
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres).

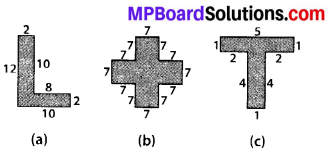
Solution:
(a) We have,

Area of rectangle ABCD = 2 × 10 cm² = 20 cm²
Area of rectangle DEFG = 10 × 2 cm² = 20 cm²
∴ Total area of the figure = (20 + 20) cm²
= 40 cm²

(b) We have,

There are 5 squares each of side 7 cm.
Area of one square = 7 × 7 cm² = 49 cm²
∴ Area of 5 squares = 5 × 49 cm² = 245 cm²

(c) We have,

Area of rectangle ABCD = 5 × 1 cm² = 5 cm²
Area of rectangle EFGH = 4 × 1 cm² = 4 cm²
∴ Total area of the figure = (5 + 4) cm²
= 9 cm²

Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm.
Solution:
(a) Area of rectangular region
= length × breadth = 100 cm × 144 cm = 14400 cm²
Area of one tile = 12 cm × 5 cm = 60 cm²

Thus, 240 tiles are required.

(b) Area of rectangular region
= length × breadth = 70 cm × 36 cm = 2520 cm²
Area of one tile = 12 cm × 5 cm = 60 cm²
∴ Number of tiles
= \(\frac{\text { Area of rectangular region }}{\text { Area of one tile }}=\frac{2520}{60}\) = 40
Thus, 42 tiles are required.

MP Board Class 6th Maths Solutions