MP Board Class 11th Maths Solutions Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण विविध प्रश्नावली
प्रश्न 1.
\(\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^{3}\) का मान ज्ञात कीजिए।
हल:

= (- 2 + 3i – i)
= – (- 2 + 2i) = 2 – 2i.
प्रश्न 2.
किन्हीं दो सम्मिश्र संख्याओं z1 और z2 के लिए सिद्ध कीजिए:
Re(z1z2) = Rez1 Rez2 – Imz1 Imz2
हल:
मान लीजिए z1 = a + ib, z2 = c + id
∴ z1z2 = (a + ib)(c + id)
= ac + adi + bci + i2bd
= (ac – ba) + (ad + bc) i [∴ i2 = – 1]
Re (z1z2) का वास्तविक भाग = ac – bd
= Rez1 Rez2 – Imz1 Imz2
यहाँ पर Rez1 का वास्तविक भाग = a, इसी प्रकार Rez2 = c
Imz1 = z1 का काल्पनिक भाग = b
इसी प्रकार Imz2 = d.
प्रश्न 3.
\(\left(\frac{1}{1-4 i}-\frac{2}{1+i}\right)\left(\frac{3-4 i}{5+i}\right)\) को मानक रूप में परिवर्तित कीजिए।
हल:
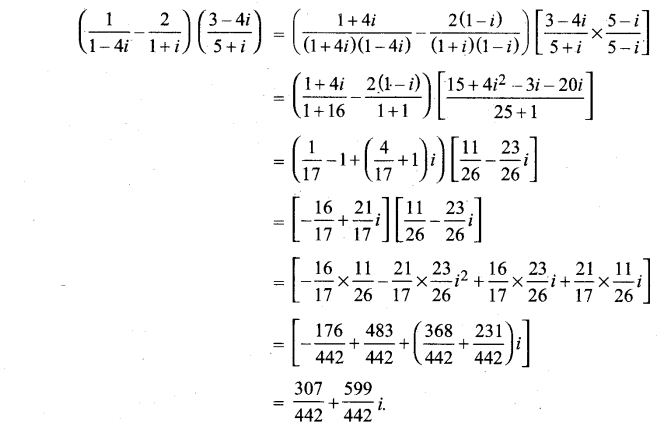
![]()
प्रश्न 4.
यदि x – iy = \(\sqrt{\frac{a-i b}{c-i d}}\), तो सिद्ध कीजिए x2 + y2 = \(\frac{a^{2}+b^{2}}{c^{2}+d^{2}}\)
हल:
x – iy = \(\sqrt{\frac{a-i b}{c-i d}}\) ….(1)

प्रश्न 5.
निम्नलिखित को ध्रुवीय रूप में परिवर्तित कीजिए:
(1) = \(\frac{1+7 i}{(2-i)^{2}}\)
(2) = \(\frac{1+3 i}{1-2 i}\)
इल:
(i) माना.
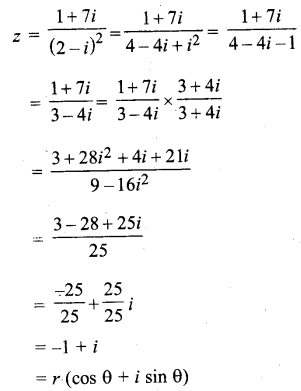
∴ r cos θ = -1, r sin θ = 1
वर्ग करके जोड़ने करने पर r2 cos2θ + r2 2θ = 1 + 1
या r2(cos2θ + sin2θ ) = 2 या r2 = 2 या r = \(\sqrt{2}\)
cos θ = ऋणात्मक, sin θ = धनात्मक
∴ 0 दूसरे चतुर्थांश में है।

(ii) \(\frac{1+3 i}{1-2 i}\)
हल:
मान लिया
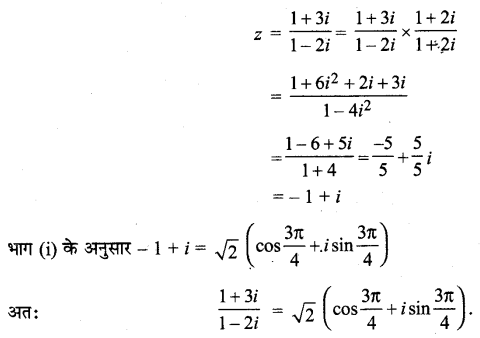
प्रश्न 6 से 9 में दिए गए प्रत्येक समीकरण को हल कीजिए:
प्रश्न 6.
3x2 4x + \(\frac{20}{3}\) = 0.
हल:
3x2 4x + \(\frac{20}{3}\) = 0 को 3 से गुणा करने पर
9x2 – 12x + 20 = 0
इसकी ax2 + bx + c = 0 से तुलना करने पर,
a = 9, b = – 12, c = 20
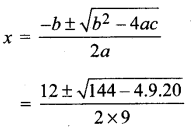

![]()
प्रश्न 7.
x2 – 2x + \(\frac{3}{2}\) = 0.
हत्त:
x2 – 2x + \(\frac{3}{2}\) = 0, इसे 2 से गुणा करने पर .
2x2 – 4x + 3 = 0
ax2 + bx + c = 0 से तुलना करने पर
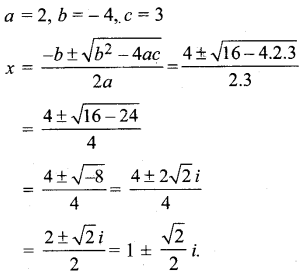
प्रश्न 8.
27x2 – 10x + 1 = 0.
हल:
दिए गए समीकरण 27x2 – 10 x + 1 = 0 की ax2 + bx + c = 0 से तुलना करने पर a = 27, b = -10, c = 1
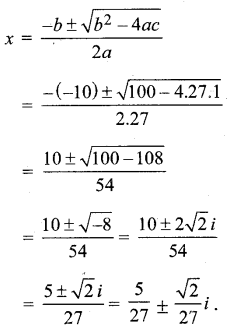
प्रश्न 9.
21x2 – 28x + 10 = 0.
हल:
21x2 – 28x + 10 = 0 की ax2 + bx + c = 0 से तुलना करने पर
a = 21, b = – 28, c = 10

![]()
प्रश्न 10.
यदि z1 = 2 -i, z2 = 1 + i, \(\left|\frac{z_{1}+z_{2}+1}{z_{1}-z_{2}+i}\right|\) का मान ज्ञात कीजिए।
हल:
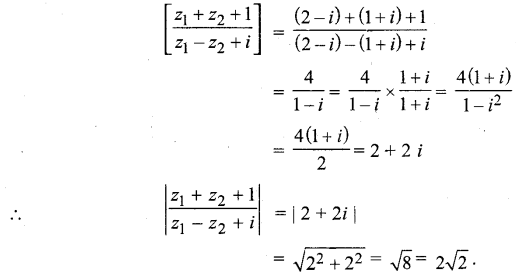
प्रश्न 11.
यदि a + ib = \(\frac{(x+i)^{2}}{2 x^{2}+1}\), सिद्ध कीजिए कि a2 + b2 = \(\frac{\left(x^{2}+1\right)^{2}}{\left(2 x^{2}+1\right)^{2}}\).
हल :
a + ib = \(\frac{(x+i)^{2}}{2 x^{2}+1}\) …..(1)
i के स्थान पर – i रखने से
a – ib = \(\frac{(x+i)^{2}}{2 x^{2}+1}\) …..(2)
समी. (1) और (2) का गुणा करने पर

प्रश्न 12.
यदि z1 = 2 – i, z2 = – 2 + i, निम्न का मान ज्ञात कीजिए :
(1) Re \(\left(\frac{z_{1} z_{2}}{\overline{z}_{1}}\right)\)
(2) Im \(\left(\frac{1}{z_{1} \overline{z}_{1}}\right)\)
हल:
(i)
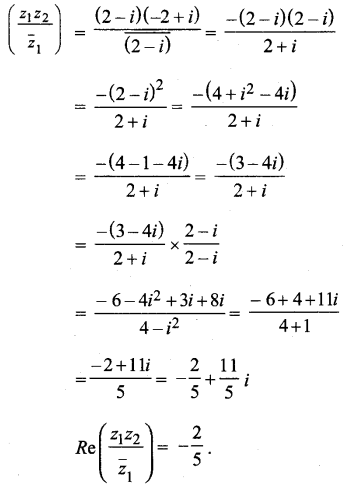
(ii) Im \(\left(\frac{1}{z_{1} \overline{z}_{1}}\right)\)
हल:
\(\frac{1}{z_{1} z_{1}}=\frac{1}{(2-i) \overline{(2-i)}}=\frac{1}{(2-i)(2+i)}\)
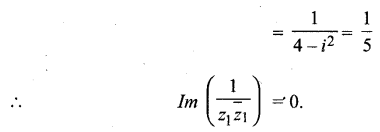
![]()
प्रश्न 13.
सम्मिश्र संख्या \(\frac{1+2 i}{1-3 i}\) का मापांक और कोणांक ज्ञात कीजिए।
हल:
माना

दोनों पक्षों की तुलना करने पर,
⇒ r cosθ = – \(\frac{1}{2}\), r sinθ = \(\frac{1}{2}\)
वर्ग करके जोड़ने पर,
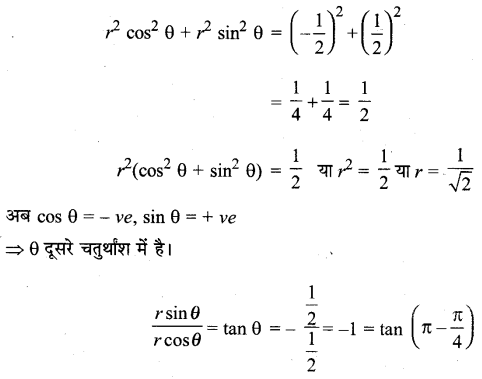

प्रश्न 14.
यदि \((x-i y)(3+5 i),-6-24 i\) की संयुग्मी है तो वास्तविक संख्याएँ x और y ज्ञात कीजिए।
हल:
\(\overline{-6-24 i}\)= – 6 + 24i ….(1)
(x – iy) (3 + 5i) = (3x – 5yi<sup.2 + 5xi – 3yi)
= 3x + 5y + (5x – 3y)i ……(2)
समीकरण (1) और (2) से,
3x + 5y + (5x – 3y)i = – 6 + 24i
वास्तविक व काल्पनिक संख्याओं को समान लिखते हुए
3x + 5y = – 6 …..(3)
5x – 3y = 24 ……(4)
समी. (3) को 3 से और समी. (4) को 5 से गुणा करने पर
9x + 15y = – 18 ….(5)
25x – 15y = 120 ….(6)
समी. (5) और समी (6) को जोड़ने पर,
34x = 102 या x = \(\frac{102}{34}\) = 3
x का मान समी. (3) में रखने पर,
9+ 5y = – 6 या 5y = – 15, या y = – 3
अतः x = 3, y = – 3.
प्रश्न 15.
\(\frac{1+i}{1-i}-\frac{1-i}{1+i}\) का मापांक ज्ञात कीजिए।
हल:

प्रश्न 16.
यदि (x + iy)3 = u + iv, तो दर्शाइए कि \(\frac{u}{x}+\frac{v}{y}=4\left(x^{2}-y^{2}\right)\).
हल:
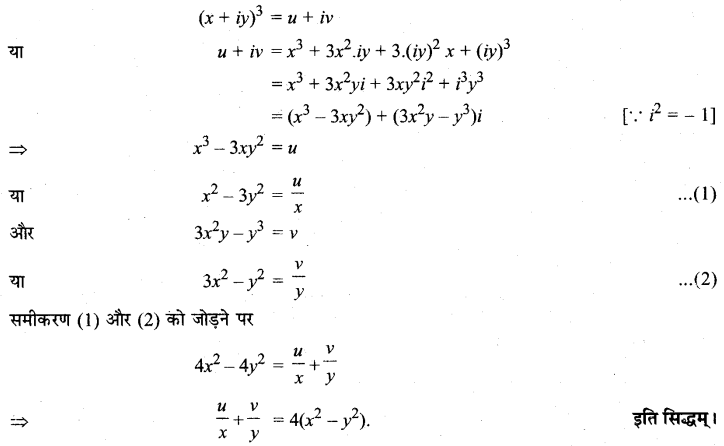
प्रश्न 17.
यदि α और β भिन्न सम्मिश्र संख्याएँ हैं जहाँ \(|\boldsymbol{\beta}|\) = 1, तब \(\left|\frac{\boldsymbol{\beta}-\boldsymbol{\alpha}}{1-\overline{\boldsymbol{\sigma}} \boldsymbol{\beta}}\right|\) का मान ज्ञात कीजिए ।
हल:

प्रश्न 18.
समीकरण \(|1-i|^{x}=2^{x}\) के शून्येत्तर पूर्णांक मूलों की संख्या ज्ञात कीजिए:
हल:
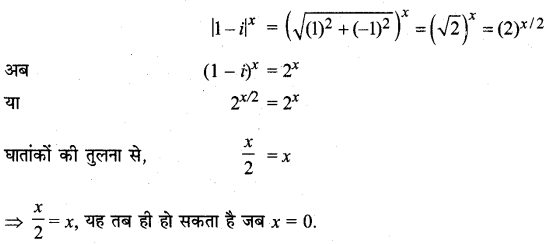
इस समीकरण का 0 के अतिरिक्त और कोई हल नहीं हो सकता।
![]()
प्रश्न 19.
यदि (a + ib)(c + id) (e + if)(g + ih) = A+iB है तो दर्शाइए कि (a2 + b2) (c2 + d2) (e2 + f2) (g2 + h2) = A2 + B2.
हल:
(a + ib) (c + id) (e + if)(g + ih) = A + iB ….(1)
i के स्थान पर – i रखने पर,
(a – ib) (c – id) (e – if)(g – ih) = A – iB …..(2)
समी (1) और (2) को गुणा करने पर,
[(a + ib) (a – ib)] [(c + id) (c – id)] [(e + if)(e – if)][(g + ih)(g – ih)] = (A + iB)(A – iB)
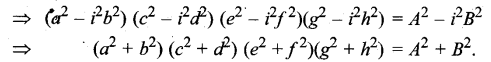
प्रश्न 20.
यदि \(\left(\frac{1+i}{1-i}\right)^{m}\) = 1, तो m का न्यूनतम पूर्णांक मान ज्ञात कीजिए।
11 1111
= 1+2+21
हल:

⇒ m संख्या 4 का गुणज है।
∴ m की कम से कम मूल्य = 4.