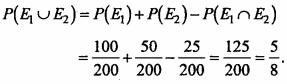MP Board Class 11th Maths Important Questions Chapter 16 Probability

MP Board Class 11th Maths Important Questions Chapter 16 Probability

Probability Important Questions

Probability Objective Type Questions

(A) Choose the correct option :

Question 1.
A leap year is selected at random. Then the probability that this year will contain 53 Sunday is :
(a) \(\frac { 1 }{ 7 }\)
(b) \(\frac { 2 }{ 7 }\)
(c) \(\frac { 3 }{ 7 }\)
(d) \(\frac { 4 }{ 7 }\)
Answer:
(b) \(\frac { 2 }{ 7 }\)

Question 2.
A and B are two events such that P(A) = 0.4, P(A + B) = 0.7, P(AB) = 0.2, then
P(B) =
(a) 0.1
(b) 0.3
(c) 0.5
(d) 0.2
Answer:
(c) 0.5

Question 3.
Three letters are to be sent to different persons and address on the three envelope are also written. Without looking at the address, the probability that the letters go into right envelope is equal to :
(a) \(\frac { 1 }{ 27 }\)
(b) \(\frac { 1 }{ 9 }\)
(c) \(\frac { 4 }{ 27 }\)
(d) \(\frac { 1 }{ 6 }\)
Answer:
(d) \(\frac { 1 }{ 6 }\)

Question 4.
If A and B are two events such that P(A ∪B) = \(\frac { 3 }{ 4 }\), P(A ∩ B) = \(\frac { 1 }{ 4 }\), P(\(\bar { A }\)) = \(\frac { 2 }{ 3 }\), then P(A ∩ B) is:
(a) \(\frac { 5 }{ 12 }\)
(b) \(\frac { 3 }{ 8 }\)
(c) \(\frac { 5 }{ 8 }\)
(d) \(\frac { 1 }{ 4 }\)
Answer:
(a) \(\frac { 5 }{ 12 }\)

Question 5.
The probability that A speaks truth is \(\frac { 4 }{ 5 }\) while that this probability for B is \(\frac { 3 }{ 4 }\). The probability that they contradict each other when asked to speak on a fact:
(a) \(\frac { 5 }{ 12 }\)
(b) \(\frac { 3 }{ 8 }\)
(c) \(\frac { 5 }{ 8 }\)
(d) \(\frac { 1 }{ 4 }\)
Answer:
(c) \(\frac { 5 }{ 8 }\)

Question 6.
A player drawn one card from a pack of 52 cards, then the probability that it is not a diamond card :
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { 2 }{ 4 }\)
(c) \(\frac { 3 }{ 4 }\)
(d) \(\frac { 1 }{ 13 }\)
Answer:
(c) \(\frac { 3 }{ 4 }\)

Question 7.
Probability of getting number greater than 3 when a dice is thrown :
(a) 1
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ 6 }\)
Answer:
(c) \(\frac { 1 }{ 2 }\)

Question 8.
A bag contain 6 white, 5 black and 4 yellow balls. The probability of drawing a white or a black ball is :
(a) \(\frac { 6 }{ 11 }\)
(b) \(\frac { 6 }{ 15 }\)
(c) \(\frac { 5 }{ 15 }\)
(d) \(\frac { 11 }{ 15 }\)
Answer:
(d) \(\frac { 11 }{ 15 }\)

Question 9.
Probability of getting an even number on throwing a dice is :
(a) 1
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ 6 }\)
Answer:
(c) \(\frac { 1 }{ 2 }\)

Question 10.
If P(A) = \(\frac { 1 }{ 4 }\), P(B) = \(\frac { 1 }{ 2 }\) and P(A ∩ B) = \(\frac { 1 }{ 8 }\) then P(A’ ∩ B’)=
(a) \(\frac { 1 }{ 8 }\)
(b) \(\frac { 3 }{ 8 }\)
(c) \(\frac { 5 }{ 8 }\)
(d) \(\frac { 7 }{ 8 }\)
Answer:
(b) \(\frac { 3 }{ 8 }\)

(B) Fill in the blanks :

1. a : b is odds in favour of an event A, then probability that it happen ………………..
2. The probability of getting odd number when a cubical dice is thrown ………………..
3. Total number of sample points when three coins are thrown are ………………..
4. It is given that the event A and B such that P(A) = \(\frac { 1 }{ 4 }\), P(\(\frac { A }{ B }\)) = \(\frac { 1 }{ 2 }\) and P(\(\frac { B }{ A }\)) = \(\frac { 2 }{ 3 }\), then P(B) = ………………..
5. If P(A) = 0.42, P(B) = 0.48, P(A ∩ B) = 0-16, then P(A’ ∩ B’) = ………………..
6. If two events A and B related to a random experiment are not mutually exclusive, then P(A ∪ B) + P(A ∩ B) = ………………..
7. Probability of happening of an event and not happening are P (A) and P(A) respectively P(A) + P(\(\bar { A }\)) = ………………..
8. The number of sample space when two cubical dice are thrown is ………………..
9. If A and B are two mutually exclusive events and P(B) = 2 P(A) then the value of P(A) will be ………………..
10. If two dice are thrown simultaneously, then the probability of getting sum is 7 will be ………………..

Answer:

1. \(\frac { a }{ a + b }\)
2. \(\frac { 1 }{ 2 }\)
3. 8
4. \(\frac { 1 }{ 3 }\)
5. 0.26
6. P(A) + P(B)
7. 1
8. 36
9. \(\frac { 1 }{ 3 }\)
10. \(\frac { 1 }{ 6 }\)

(C) Write true / false :

1. If two coins are tossed together, then the probability of getting atleast one head is \(\frac { 3 }{ 4 }\).
2. From a pack of cards one card is drawn at random then the chance of getting knave \(\frac { 1 }{ 52 }\)
3. If tossing a coin once, then the probability of getting tail on the upper face is \(\frac { 1 }{ 2 }\)
4. If two dice are thrown simultaneously, then the probability of getting product 6 is \(\frac { 1 }{ 9 }\)
5. The odds favour in event is \(\frac { 3 }{ 4 }\), then the probability of happening is \(\frac { 4 }{ 7 }\)

Answer:

1. True
2. False
3. True
4. True
5. False

(D) Write answer in one word / sentence :

1. If two coins are tossed together, then the sample space will be?
2. From a well shuffled pack of 52 cards one card is drawn at random; find the probability it is a king.
3. Two dice are thrown simultaneously, find the probability getting sum is multiple of 3.
4. The odds in favour of an event is 3 : 5, then find the probability of not happening.
5. If A, B and C are three mutually exclusive even, then P(A ∪ B ∪ C) =

Answer:

1. {HT, HH, TH, TT}
2. \(\frac { 1 }{ 13 }\)
3. \(\frac { 1 }{ 3 }\)
4. \(\frac { 5 }{ 8 }\)
5. P(A) + P(B) + P(C )

Probability Short Answer Type Questions

Question 1.
A coin is tossed twice, what is the probability that at least one tail occurs? (NCERT)
Solution:
Let S is the sample space, then
S = {(H, H), (H, T), (T, H), (T, T)}
n(S) = 4
Let E be the event of getting at least one tail, then
E = {(H, T), (T, H), (T, T)}
∴ n(E) = 3
Hence, required probability P(E) = \(\frac { n(E) }{ n(S) }\) = \(\frac { 3 }{ 4 }\)

Question 2.
There are four men and six women on the city council. If one council member is selected for a committee at random, then how likly is it that it is a woman?
Solution:
Let S is the sample space, then
n (S) = 10
Let E be the event that woman is selected, then
n(E) = 6
Hence, required probability P(E) = \(\frac { n(E) }{ n(S) }\)
P(E) = \(\frac { 6 }{ 10 }\) = \(\frac { 3 }{ 5 }\)

Question 3.
If \(\frac { 2 }{ 11 }\) is the probability of an event A, then find what is the probability of the event is ‘not A’.
Solution:
Given that :
P(A) = \(\frac { 2 }{ 11 }\)
We know that,
P(A) + P(\(\bar { A }\)) = 1
\(\frac { 2 }{ 11 }\) + P(\(\bar { A }\)) = 1
P(\(\bar { A }\)) = 1 – \(\frac { 2 }{ 11 }\) = \(\frac { 11 – 2 }{ 11 }\)
P(\(\bar { A }\)) = \(\frac { 9 }{ 11 }\).

Question 4.
A box contain 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box. What is the probability that: (NCERT)

1. All marbles will be blue.
2. At least one marble will be green.

Solution:
In the box, there are 10 red, 20 blue and 30 green marbles.
The No. of marbles = 10 + 20 + 30 = 60
1. Total ways of choosing 5 marbles out of 60 marbles,
n(S) = ⁶⁰C₅
Let E is the event of choosing blue marbles, then
n(E) = ²⁰C₅
Probability = \(\frac { n(E) }{ n(S) }\) = \(\frac{^{20} C_{5}}{^{60} C_{5}}\)

2. P(At least one green marble)
= 1 – P(No green)
= 1 – \(\frac{^{30} C_{5}}{^{60} C_{5}}\)

Question 5.
4 cards are drawn from a well shuffled deck of 52 cards. What is the probability of obtaining in card of 3 diamond and one spade?
Solution:
Let S is the sample space.
Total number of selecting 4 cards out of 52 cards, n(S) = ⁵²C₄
If E is the event obtaining card of 3 diamond and 2 spade, then
n(E) = ¹³C₃ x ¹³C₁
Probability P(E) = \(\frac { n(E) }{ n(S) }\) = \(\frac{^{13} C_{3} \times^{13} C_{1}}{^{52} C_{4}}\)

Question 6.
Given : P(A) = \(\frac { 3 }{ 5 }\) and P(B) = \(\frac { 1 }{ 5 }\). If A and B are mutually exclusive events, then find P(A or B). (NCERT)
Solution:
A and B are mutually exclusive events.
∴ P (A or B) = P(A ∪ B) = P(A) + P(B)
P(A ∪ B) = \(\frac { 3 }{ 5 }\) + \(\frac { 1 }{ 5 }\) = \(\frac { 3 + 1 }{ 5 }\) = \(\frac { 4 }{ 5 }\)

Question 7.
In a lottery, a person choose six different natural numbers at random from 1 to 20 and if there six numbers match with the six numbers already fixed by lottery committee, he wins the prize, what is the probability of winning the prize in the game? (Hint: Order of the numbers is not important) (NCERT)
Solution:
Let S is the sample space, then
n(S) = ²⁰C₆
= \(\frac { 20 × 19 × 18 × 17 × 16 × 15 }{ 6 × 5 × 4 × 3 × 2 × 1 }\) = 38760
Only one prize can be win.
∴ n(E) = 1
Hence, required probability P(E) = \(\frac { n(E) }{ n(S) }\) = \(\frac { 1 }{ 38760 }\)

Question 8.
Two dice are thrown simultaneously. Find the probability of getting a sum 9 in a single throw.
Solution:
Total number of ways in which two dice may be thrown
= 6 x 6 = 36
∴ n(S) = 36
Event of getting sum 9 is A = {(3, 6), (4, 5), (5, 4), (6, 3)}
∴ n(A) = 4
∴ Required probability P(A) = \(\frac { n(A) }{ n(S) }\) = \(\frac { 1 }{ 9 }\)

Question 9.
A bag contains 8 black, 6 white and 5 red balls. Find the probability of drawing a black or a white ball from it
Solution:
Total number of balls = 8 + 6 + 5 = 19
∴ n(S) = 19
Event A of drawing 1 black or 1 white ball
n(A) = 8 + 6 = 14
∴ n(A) = 14
∴ Required probability P(A) = \(\frac { n(A) }{ n(S) }\) = \(\frac { 14 }{ 19 }\)

Question 10.
From a pack of well shuffled cards two cards drawn simultaneously. Find the probability that both the cards are ace.
Solution:
Total number of ways of drawing two cards out of 52
= ⁵²C₂
Number of ways drawing two ace out of 4 ace
= ⁴C₂
∴ Required Probability

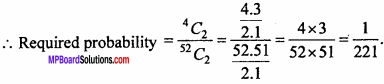
Question 11.
A pair of dice are thrown. Find the probability that the sum is 9 or 11.
Solution:
Let the sample space be S, then
∴ n(S) = 36
Let E be the event that sum is 9 or 11, then
E = {(5, 4), (4, 5), (6, 3), (3, 6), (6, 5), (5, 6)}
∴ n (E) = 6
The probability of getting sum 9 or 11 is
P(E) = \(\frac { n(E) }{ n(S) }\) = \(\frac { 6 }{ 36 }\) = \(\frac { 1 }{ 6 }\)
Hence, probability that the sum is not 9 or 11 is
P(\(\bar { E }\)) = 1 – P(E)
= 1 – \(\frac { 1 }{ 6 }\) = \(\frac { 5 }{ 6 }\)

Question 12.
In a city 20% persons read English newspaper, 40% persons read Hindi newspaper and 5% persons read both, then find the probability that the newspapers are not read.
Solution:
P(E) = The probability that persons read English newspapers = \(\frac { 20 }{ 100 }\)
p(H) = The probability that persons read Hindi newspapers = \(\frac { 40 }{ 100 }\)
P(E ∩ H) = The probability that persons read both the papers = \(\frac { 5 }{ 100 }\)
The probability that the newspapers are not read

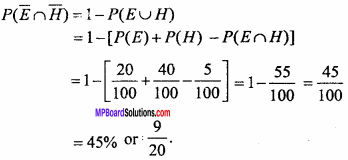
Question 13.
In class XI of a school, 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology. (NCERT)
Solution:
Let M and B denote the students of Mathematics and Biology respectively. Then, as given:
P(M) = 40% = \(\frac { 40 }{ 100 }\)
= P(B) = 30% = \(\frac { 30 }{ 100 }\)
P(M ∩ 5) = 10% = \(\frac { 10 }{ 100 }\)
∴ P(M ∪ B) = P(M) + P(B) – P(M ∩ B)
\(\frac { 40 }{ 100 }\) + \(\frac { 30 }{ 100 }\) – \(\frac { 10 }{ 100 }\)
= \(\frac { 60 }{ 100 }\) = 60% = 0.6.

Question 14.
In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing at least one of them is 0.95. What is the probability of passing both? (NCERT)
Solution:
Let probability of passing in first examination is A and passing in the second examination is B.
P(A) = 0.8, P(B) = 0.7, P(A ∪ B) = 0.95, P(A ∩ B) = ?
We know that,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
0.95 = 0.8 + 0.7 – P(A ∩ B)
⇒ P(A ∩ B) = 1.5 – 0.95
∴ P(A ∩ B) = 0.55.

Probability Long Answer Type Questions

Question 1.
A letter is selected at random from the word ‘ASSASSINATION’. Find the probability that letter is

1. a vowel
2. a consonant

Solution:
Number of letters is 13 in which there are 6 vowels and 7 consonants.
1. Let sample space is S, then
∴ n(S) = 13
E₁ is the event of choosing a vowel, then
n(E₁) = 6
Hence, required probability P(E₁) = \(\frac{n\left(E_{1}\right)}{n(S)}\)
P(E₁) = \(\frac { 6 }{ 13 }\)

2. E₂ is the event of choosing a consonant, then
n(E₁) = 7
Hence, required probability P(E₂) = \(\frac{n\left(E_{2}\right)}{n(S)}\)

Question 2.
Check whether the following probabilities P{A) and P(B) are consistently defined: (NCERT)

1. P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
2. P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8.

Solution:
1. Given : P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
If P(A ∩ B) ≤ P(A) and P(A ∩ B) ≤ P(B)
Then, P(A) and P(B) are consistent.
Here

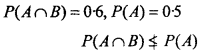
P(A) and P(B) are not consistent.

2. Given : P(A) = 0.5, P(B) = 0 4, P(A ∪ B) = 0.8

∴ P(A) and P(B) are consistent.

Question 3.
In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that:

1. The student opted for NCC or NSS.
2. The student has opted for neither NCC nor NSS.
3. The student has opted NSS but not NCC.

Solution:
Let A and B denote the students in NCC and NSS respectively.
Given : n(A) = 30, n(B) = 32, n(S) = 60, n(A ∩ S) = 24

1. P (Student opted for NCC or NSS)

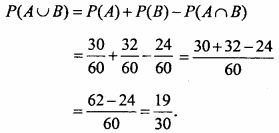
2. P (Student has opted neither NCC nor NSS)

3. P (The student has opted NSS but not NCC)

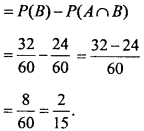
Question 4.
From the employees of a company, 5 persons are selected to represent them in managing committee of the company. Particulars of five persons are as follows :

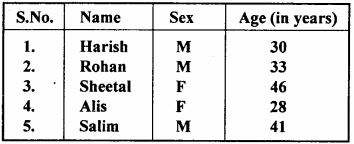
A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 years? (NCERT)
Solution:
Let A is the event that selected person is male and B be the event that selected person is over 35 years.

Hence, required probability
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac { 3 }{ 5 }\) + \(\frac { 2 }{ 5 }\) – \(\frac { 1 }{ 5 }\) = \(\frac { 3 + 2 – 1 }{ 5 }\) = \(\frac { 4 }{ 5 }\)

Question 5.
A fair coin with 1 marked on one face and 6 on the other and a fair dice are both tossed. Find the probability that the sum of the numbers that turn up is: (NCERT)

1. 3
2. 12.

Solution:
The number of possible cases in coin = 2 Number of possible cases in dice = 6 Let S is the sample space, then
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 12
1. Let E is the event of coming sum of the numbers as 3, then
E = { 1, 2 }
∴ n(E) = 1
Required probability P(E) = \(\frac { n(E) }{ n(S) }\) = \(\frac { 1 }{ 12 }\)

2. Let E’ is the event of coming sum of the numbers as 12, then E’ = (6, 6)
∴ n(E’) = 1
Required probability P(E’) = \(\frac { n(E’) }{ n(S) }\) = \(\frac { 1 }{ 12 }\)

Question 6.
In a certain lottery 10,000 tickets are sold and ten equal prizes are awarded. What is the probability of not getting a prize if you buy?

1. One ticket
2. Two tickets
3. 10 tickets.

Solution:
1. Buying one ticket:
Total tickets = 10,000
The tickets getting not prize = 10,000 – 10 = 9,990
Let S is the sample space, then
n(S) = ^10,000C₁ = 10,000
Let E₁ is the event of not getting prize on buying one ticket, then
n(E₁) = ^9,990C₁ = 9,990
∴ Required probability P(E₁) = \(\frac{n\left(E_{1}\right)}{n(S)}\) = \(\frac { 9, 990 }{ 1, 000 }\) = \(\frac { 999 }{ 1, 000 }\)

2. On buying two tickets, then
n(S) = ^10,000C₂
Let E₂ is the event of not getting prize on buying two tickets, then
n(E₂) = ^9,990C₂
∴ Required probability P(E₂) = \(\frac{n\left(E_{2}\right)}{n(S)}\) = \(\frac { 9, 990 }{ 1, 000 }\)

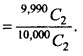
3. On buying 10 tickets, then
n(S) = ^10,000C₁₀
Let E₃ is the event of not getting prize on buying ten tickets, then
n(E₃) = ^9,990C₁₀
∴ Required probability P(E₃) = \(\frac{n\left(E_{3}\right)}{n(S)}\)

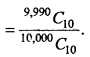
Question 7.
A bag contains 50 bolts and 150 nuts. Half of the bolts and nuts are rusted. If one item is taken out at random. Find out the probability that it is rusted or is a bolt.
Solution:
Let S be the sample space, then
∴ n (S) = 200, [∵ 50 bolt + 150 nuts = 200]
According to the question half of the bolts and nuts are rusted.
∴ Total rusted article = 25 + 75 = 100
Let E₁ is the event of drawing a rusted article.
Then, P(E₁) = \(\frac{n\left(E_{1}\right)}{n(S)}\) = \(\frac { 100 }{ 200 }\)
Let E₂ is the event of drawing nuts.
Then, P(E₂) = \(\frac{n\left(E_{2}\right)}{n(S)}\) = \(\frac { 50 }{ 200 }\)
In both the events E₁, and E₂, 25 rusted bolts are common.

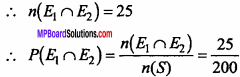
Hence, required probability

MP Board Class 11th Maths Important Questions